статисика
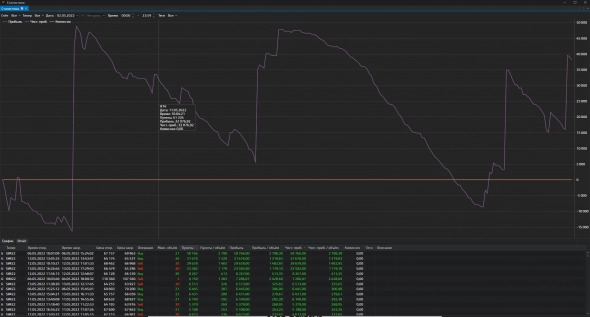
Статистика за 2 недели торгов с 02.05 по 13.05
- 13 мая 2022, 19:34
- |
Качество картинки человеческое а не смартлабовское
Тут качество prnt.sc/in2OcvD10hNL
Тут отрицательная сортировка prnt.sc/TE_DZ7ZioSh3
Тут общая по сделкам prnt.sc/pMJXqEce1GJ5
Покачала на этой недели тяжелые торги
И того + 38 000 на таком сумбурном сложном рынке. один из счетов
Конечно результаты могли быть и + 130 000, торги прошли так как прошли
Всем хороших выходных
Делитесь своей статистикой!!
Я в телеграмме https://t.me/VitalyPTSS
Частная группа telegram https://t.me/+Cs7dP8x8TvwxNGVi
Мой торговый терминал https://tiger-trade.g2afse.com/click?...
- комментировать
- 198
- Комментарии ( 0 )
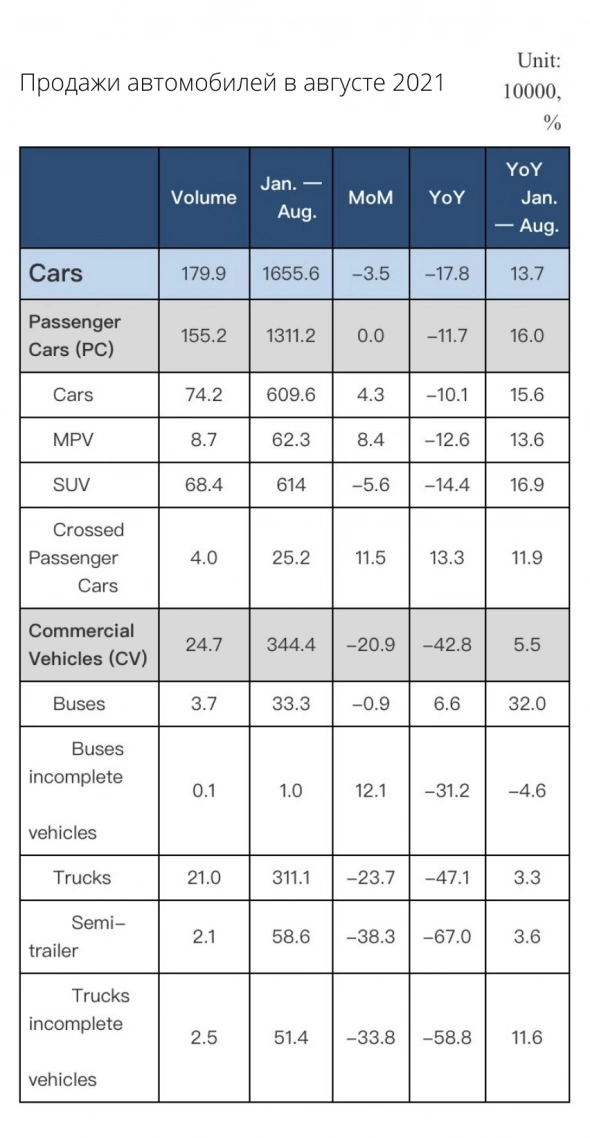
промышленноепроизводство китая +7,5%прогноз 3,9%. интрига в преддверии заседания фрс
- 15 марта 2022, 11:54
- |
Почему дневные изменения цен акций не следуют Распределению Парето?
- 20 сентября 2021, 23:10
- |
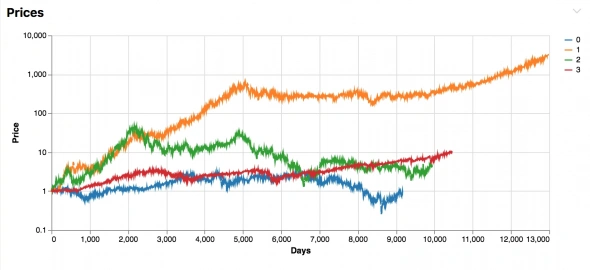
Я рассчитал распределение изменений цены акций (дифф). Имеются ввиду мультипликативны изменения (diff), во сколько раз меняется цена акции за каждый день, d(t) = p(t) / p(t-1)
Насколько я знаю, распределение должно выглядеть как распределение по Power law (распределение Парето). С CDF, являющейся линией на графике log-log.
Но CDF который я получил не похож на линию на графике log-log. Почему?
Mожет ли это быть вызвано тем, что распределение имеет два хвоста вместо одного? Поскольку имеются два редких событий: редкие огромные ежедневные падения цен с d <0,7 и редкие огромные ежедневные повышения цен d > 1,4
Насколько мне известно, линейный тест распределения парето на логлог графике используется для распределений с одним хвостом. Как например распределение богатства у людей. Можно ли его также использовать для распределения с двумя хвостами?
Пример
Ежедневные цены на 4 акции за пару лет, нормированные на 1 за первый день.
( Читать дальше )
Статистика: что и как считать (на примере Франции)
- 14 сентября 2021, 12:28
- |
Завтра 15 сентября, и по новым правилам, в сфере здравоохранения все работники должны пройти вакцинацию. В преддверии этого события вчера по тому же каналу показали репортаж о службе скорой помощи, в которой за последние две недели вынужденно уволились (согласно официальным данным) 10% работников, вызвав паралич системы неотложной помощи. Это те люди, которые ни под каким предлогом не захотели прививаться. В срочном порядке ищут новых работников им на замены, с предложением Министерству здравоохранения облегчить тестирование при приему на работу в этом секторе.
Что и как считать в нужный момент времени является решающим фактором для огласки данных широкой публике.
Обзор календаря на сегодня (2 август 2021 г.)
- 02 августа 2021, 13:56
- |
Казнь, гильотина. Осужденный поднимает голову и спрашивает у палача:
— А какой сегодня день?
— Понедельник!
— Ну, блин и начинается неделька...
Еще разок добрый день дорогие читатели, ну может быть у главного героя понедельник не очень так и задался, а вот у Австралийцев и Канадцев сегодня выходной! Как по традиции начнем мы рабочий день с того, что быстренько пробежимся по календарю макроэкономической статистики!
Сегодня большинство стран мира будут публиковать свои данные по индексу деловой активности (PMI — Purchasing Managers’ Index) в число этих стран входят: Япония, Китай, Швейцария, сама еврозона в целом, Германия, Франция, а также Америка.
Важно отметить, что на ряду с индексом деловой активности Швейцария сегодня с нами поделиться такими данными, как розничные продажи и индексом потребительских цен.
Сказать бы честно, сегодня я бы ни одно событие не назвал бы важным кроме отдыха Канады, что в свою очередь внесет немного спокойствие на рынок нефти. Даже не особо верится в то, что Американские данные по PMI смогут повлиять на рынок.
( Читать дальше )
Обзор фичи будущей версии Investbook 2021.5
- 27 мая 2021, 23:38
- |
1. Таблица "Срочный рынок" отображает доходность (вариационную маржу) по каждому контракту за каждый день владения.
2. Таблица "Портфель" отображает суммированную вариационную маржу по каждому срочному контракту, например доход по Si-3.21 = итого 1000 руб, Si-6.21 = итого 500 руб без разбивки по дням, с учетом текущей котировки.
В версии 2021.5 добавляется новая таблица «Портфель трейдера», которая будет отображает прибыль, полученную по группе контрактов, например всех фьючерсов и опционов Si с любой датой экспирации.
Таблица показывает итоговую прибыль и полезна, если вы:
— используете опционные стратегии, например стрэддл, стрэнгл и др., составленные из нескольких контрактов одной группы;
— переносите позицию из экспирируемого контракта в следующий контракт, например из Si-6.21 в Si-9.21;
( Читать дальше )
Investbook. Голосование на фичи следующего релиза
- 04 мая 2021, 14:28
- |
Прямо сейчас и до ближайших выходных проводится общее собрание пользователей. На собрании обсуждаются функционал, который пользователи хотели бы видеть в следующей версии приложения. Вы можете поучаствовать и предложить свои фичи, участвовать в развитии продукта «под себя». Функционал будет выбран посредством голосования. Все, включая разработчиков, имеют равные голоса.
Ссылка на голосование.
Топ запрошенных инвесторами тем

Релиз журнала сделок Investbook 2021.4.1
- 04 мая 2021, 01:01
- |
— Исправлено отображение «Доходности, %» валютных активов в таблице Портфель.
— ВТБ Брокер: доработан парсер Активов (учтены вариации в формате отчета брокера).
— Уралсиб Брокер: для долларовых облигаций исправлено сохранение котировок.
Подробнее о возможностях.
Ссылка на GitHub для скачивания установщика/апдейтера.
Страница софта на Smartlab.
Telegram чат технической поддержки.
Investbook — это локальное (десктопное) бесплатное приложение для ведение журнала сделок с возможностью парсинга отчетов брокера (альтернатива ручному внесению сделок в журнал). Поддерживаются парсеры отчетов брокеров ВТБ, ПСБ, Уралсиб, Сбербанк по остальным брокерам сделки можно вводить вручную.

- bitcoin
- brent
- eurusd
- forex
- gbpusd
- gold
- imoex
- ipo
- nasdaq
- nyse
- rts
- s&p500
- si
- usdrub
- wti
- акции
- алготрейдинг
- алроса
- аналитика
- аэрофлот
- банки
- биржа
- биткоин
- брокеры
- валюта
- вдо
- волновая разметка
- волновой анализ
- волны эллиотта
- вопрос
- втб
- газ
- газпром
- гмк норникель
- дивиденды
- доллар
- доллар рубль
- евро
- золото
- инвестиции
- индекс мб
- инфляция
- китай
- кризис
- криптовалюта
- лукойл
- магнит
- ммвб
- мобильный пост
- мосбиржа
- московская биржа
- мтс
- натуральный газ
- нефть
- новатэк
- новости
- обзор рынка
- облигации
- опрос
- опционы
- отчеты мсфо
- офз
- оффтоп
- прогноз
- прогноз по акциям
- путин
- раскрытие информации
- ри
- роснефть
- россия
- ртс
- рубль
- рынки
- рынок
- санкции
- сбер
- сбербанк
- северсталь
- смартлаб
- сущфакты
- сша
- технический анализ
- торговля
- торговые роботы
- торговые сигналы
- трамп
- трейдинг
- украина
- фондовый рынок
- форекс
- фрс
- фьючерс
- фьючерс mix
- фьючерс ртс
- фьючерсы
- цб
- цб рф
- экономика
- юмор
- яндекс


















 Новости тг-канал
Новости тг-канал