Избранное трейдера tester37
В IT через алго. ОГЛАВЛЕНИЕ и дисклеймер. Коннекторы к OsEngine #0
- 14 ноября 2023, 15:12
- |
Обновляемый пост с оглавлением серии «Коннекторы к OsEngine».
Камрады, добавляем в избранное. Буду ссылку на данный пост добавлять к каждой статье из серии, чтобы люди, видящие внезапно 21 часть – могли пройти сюда и ознакомится с полным содержанием и смыслами. А Вы раз в неделю сможете открывать данный пост, если не следите каждый день за нашим блогом, и сможете увидеть, что новенького.
Проблема
Чтобы зарабатывать деньги на бирже, нужен либо первоначальный капитал, либо возможность откладывать деньги на инвестиции стабильно и каждый месяц. Без этого не возможны никакие подходы к торговле. Ни дивидендное инвестирование, ни алготрейдинг.
Насколько бы удачливым и прозорливым трейдером ты не был, если у тебя на счету 100 / 300 тысяч рублей и откладывать ты не можешь – никаких денег на бирже ты скорее всего не заработаешь. Об этом мало кто говорит, но это так. Маленькие счета провоцируют на нарушение риска, даже алготрейдера. Что почти гарантированно ведёт к потере денег, а не к прибыли.
( Читать дальше )
- комментировать
- 8.8К | ★23
- Комментарии ( 1 )
Основы статистического арбитража. Коинтеграция.
- 27 апреля 2012, 21:16
- |
Рассмотрим для начала простейший процесс, гауссовский шум:
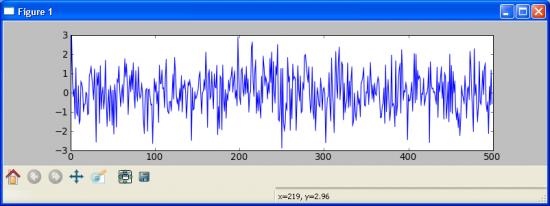
Теперь построим его кумулятивную сумму, то есть возьмем значения и последовательно их сложим, таким образом получим что Y_i = sum k = 0..i X_k, где X_k — это исходный гаусовский шум, Y_i — результирующий процесс. То есть в данном случаи взяли шум и его проинтегрировали, таким образом получив случайное блуждание. Так же мы можем повторить данный процесс еще раз, но на этот раз взяв в качестве исходных значений, полученное нами на предыдущем шаги случайное блуждание. Таким образом получим (сверху — интеграл шума, случайное блуждание, снизу — повторная сумма но на этот раз взятая по случайному блужданию):
( Читать дальше )
- bitcoin
- brent
- eurusd
- forex
- gbpusd
- gold
- imoex
- ipo
- nyse
- s&p500
- si
- usdrub
- акции
- алготрейдинг
- алроса
- анализ
- аналитика
- аэрофлот
- банки
- биржа
- биткоин
- брокеры
- валюта
- вдо
- волновая разметка
- волновой анализ
- вопрос
- втб
- газ
- газпром
- гмк норникель
- дивиденды
- доллар
- доллар рубль
- дональд трамп
- евро
- золото
- инвестиции
- инвестиции в недвижимость
- индекс мб
- инфляция
- китай
- ключевая ставка цб рф
- кризис
- криптовалюта
- лукойл
- магнит
- ммвб
- мобильный пост
- мосбиржа
- московская биржа
- мтс
- натуральный газ
- нефть
- новатэк
- новости
- обзор рынка
- облигации
- опрос
- опционы
- отчеты мсфо
- офз
- оффтоп
- прогноз
- прогноз по акциям
- путин
- раскрытие информации
- роснефть
- россия
- ртс
- рубль
- рынки
- рынок
- санкции
- сбер
- сбербанк
- северсталь
- смартлаб
- сущфакты
- сша
- технический анализ
- торговля
- торговые роботы
- торговые сигналы
- трамп
- трейдинг
- украина
- фондовый рынок
- форекс
- фрс
- фьючерс
- фьючерс mix
- фьючерс ртс
- фьючерсы
- цб
- цб рф
- экономика
- экономика россии
- юмор
- яндекс


















 Новости тг-канал
Новости тг-канал

