SMART-LAB
Новый дизайн
Мы делаем деньги на бирже
Блог им. SerSer |Автоматизация трендов | обновление
- 25 сентября 2018, 16:22
- |
Перелопатил код и обновил свои индикаторы по автоматизации построения трендов.
Заменил линейную регрессию на экспоненциальную, подшаманил с алгоритмами гомоскедастичностью и робастностью, прочие баги...
В общем продолжу традицию экипировки молодых бойцов ЛЧИ )))
Каналы
было - https://smart-lab.ru/blog/386529.php
стало
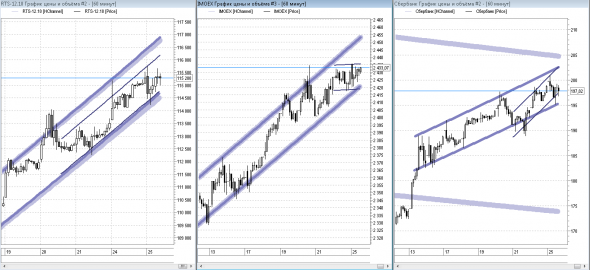
( Читать дальше )
Заменил линейную регрессию на экспоненциальную, подшаманил с алгоритмами гомоскедастичностью и робастностью, прочие баги...
В общем продолжу традицию экипировки молодых бойцов ЛЧИ )))
Каналы
было - https://smart-lab.ru/blog/386529.php
стало

( Читать дальше )
- комментировать
- ★33
- Комментарии ( 26 )
Блог им. SerSer |Фазы тренда | QUIK | Индикатор
- 02 июня 2017, 14:16
- |
1. Теория
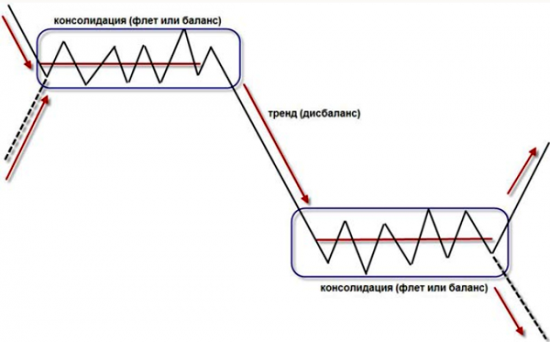
Фазы рынка/тренда. Метод Вайкоффа.
( Читать дальше )
Фазы рынка/тренда. Метод Вайкоффа.

Суть метода Вайкоффа состоит в том, что крупный игрок не может просто купить или продать по рынку столько актива, сколько ему нужно, поэтому он использует для набора позиций узкие зоны консолидации, а потом начинает толкать рынок в нужную ему сторону, где он скинет набранный объем.
В момент, когда крупный игрок набирает позицию, на рынке наблюдается фаза баланса.
Ну а тренд – это дисбаланс.
Соответственно, если понять и принять такую структуру рынка, то несложно определить – цена всегда ходит в широком боковике, двигаясь от баланса к балансу.
( Читать дальше )
Блог им. SerSer |Любимая рабочая лошадка с новыми подковами.
- 06 февраля 2017, 12:09
- |
Портировал из LUA в машинный код, один из любимых рабочих инструментов.
Аццкая смесь Homoscedasticity, Fractal dimension и некоторых «секретных ингредиентов» Probability theory, породившая приемлемый Support and Resistance, не зависящий от субъективности и настроений «прокладки» между рынком и кошельком.
Пока была в LUA больше 3-4 запустить не получалось, не «повесив» QUIK, а сейчас:
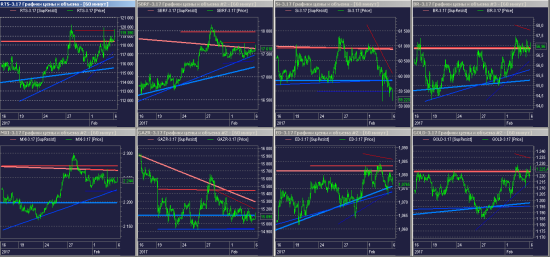
( Читать дальше )
Аццкая смесь Homoscedasticity, Fractal dimension и некоторых «секретных ингредиентов» Probability theory, породившая приемлемый Support and Resistance, не зависящий от субъективности и настроений «прокладки» между рынком и кошельком.
Пока была в LUA больше 3-4 запустить не получалось, не «повесив» QUIK, а сейчас:

( Читать дальше )
Блог им. SerSer |QUIK, LUA, Робастность и прочее...
- 02 февраля 2017, 14:31
- |
Зачитался, я тут на днях про робастную регрессию, и очень мне захотелось «пощупать» этого зверя хоть в каком нибудь виде на графике в Квике.
Выбрал наипростейшую — "Оценочная функция Тейла – Сена"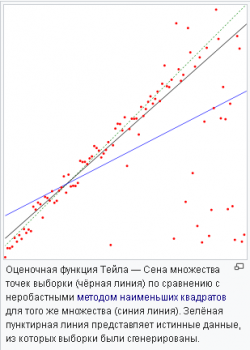
Сказано — сделано.
( Читать дальше )
Выбрал наипростейшую — "Оценочная функция Тейла – Сена"
Эта оценочная функция может быть эффективно вычислена и она нечувствительна к выбросам. Она может быть существенно более точна, чем неробастный метод наименьших квадратов для несимметричных и гетероскедастичных данных и хорошо конкурирует с неробастным методом наименьших квадратов даже для нормально распределенных данных в терминах статистической мощности.
Метод признан «наиболее популярной непараметрической техникой оценки линейного тренда»

Сказано — сделано.
( Читать дальше )
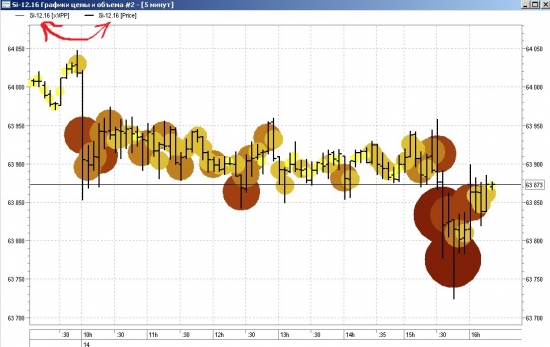
Блог им. SerSer |Индикатор Горизонтальных объемов | LUA QUIK
- 07 ноября 2016, 18:40
- |
Индикатор работает в рамках ограничений/возможностей QLUA и простоты использования, поэтому не обессудьте.
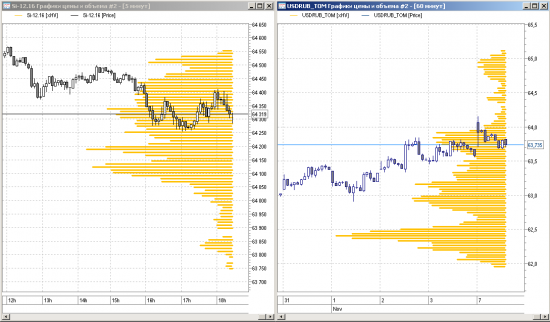
( Читать дальше )

( Читать дальше )
Блог им. SerSer |Индикатор фрактальной размерности | LUA
- 07 октября 2016, 15:50
- |
Упрощенный алгоритм вычисления приближенного значения размерности Минковского, для ценового ряда.
Краткая справка:
Размерность Минковского — это один из способов задания фрактальной размерности ограниченного множества в метрическом пространстве, определяется следующим образом:Размерность Минковского имеет так же другое название — box-counting dimension, из-за альтернативного способа ее определения, который кстати дает подсказку к способу вычисления этой самой размерности. Рассмотрим двумерный случай, хотя аналогичное определение распространяется и на n-мерный случай. Возьмем некоторое ограниченное множество в метрическом пространстве, например черно-белую картинку, нарисуем на ней равномерную сетку с шагом ε, и закрасим те ячейки сетки, которые содержат хотя бы один элемент искомого множества.Далее начнем уменьшать размер ячеек, т.е. ε, тогда размерность Минковского будет вычисляться по вышеприведенной формуле, исследуя скорость изменения отношения логарифмов.
- где N(ε) минимальное число множеств диаметра ε, которыми можно покрыть исходное множество.
( Читать дальше )
Блог им. SerSer |Простенький реверсивный индикатор (QLUA)
- 16 августа 2016, 15:49
- |
Реверсивный индикатор на основе EMA с простым алгоритмом исполнения.
Всем кто хочет пользоваться — Пользуйтесь!
Всем кто хочет модернизировать — Пользуйтесь!
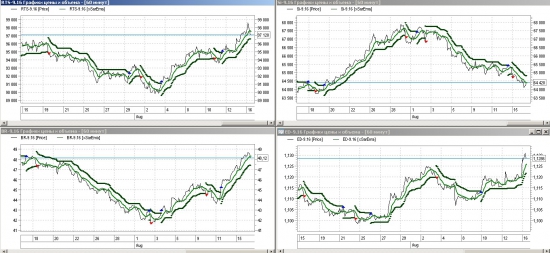
PS
Не грааль!!!
( Читать дальше )
Всем кто хочет пользоваться — Пользуйтесь!
Всем кто хочет модернизировать — Пользуйтесь!

PS
Не грааль!!!
( Читать дальше )
- bitcoin
- brent
- eurusd
- forex
- gbpusd
- gold
- imoex
- ipo
- nasdaq
- nyse
- rts
- s&p500
- si
- usdrub
- wti
- акции
- алготрейдинг
- алроса
- аналитика
- аэрофлот
- банки
- биржа
- биткоин
- брокеры
- валюта
- вдо
- волновой анализ
- волны эллиотта
- вопрос
- втб
- газ
- газпром
- гмк норникель
- дивиденды
- доллар
- доллар рубль
- евро
- золото
- инвестиции
- индекс мб
- инфляция
- китай
- кризис
- криптовалюта
- лукойл
- магнит
- ммвб
- мобильный пост
- мосбиржа
- московская биржа
- мтс
- натуральный газ
- нефть
- новатэк
- новости
- обзор рынка
- облигации
- опрос
- опционы
- отчеты мсфо
- офз
- оффтоп
- прогноз
- прогноз по акциям
- путин
- раскрытие информации
- ри
- роснефть
- россия
- ртс
- рубль
- рынки
- рынок
- санкции
- сбер
- сбербанк
- северсталь
- сигналы
- смартлаб
- сущфакты
- сша
- технический анализ
- торговля
- торговые роботы
- торговые сигналы
- трамп
- трейдинг
- украина
- фондовый рынок
- форекс
- фрс
- фьючерс
- фьючерс mix
- фьючерс ртс
- фьючерсы
- цб
- цб рф
- экономика
- юмор
- яндекс