Блог им. Kot_Begemot |Обобщённый подход к диверсификации рисков
- 28 августа 2019, 04:47
- |
- Обобщённая проблема
Результаты оценки любых случайных величин представляют из себя случайную величину. Не исключением здесь будут оценки ковариации.
Особенно сильно эффект неточности полученных оценок (случайности статистик) будет проявляться в портфелях, составленных из большого количества ценных бумаг — большего или сопоставимого количеству располагаемых наблюдений. И, поскольку, в некотором приближении задача портфельного инвестирования сводится к поиску двух максимально независимых активов из множества:
где R — коэффициент взаимной корреляции — её решение, естественным образом, будет располагаться в области максимально отрицательной статистической ошибки.
( Читать дальше )
- комментировать
- ★9
- Комментарии ( 40 )
Блог им. Kot_Begemot |Портфельная оптимизация как бустинг на «слабых» моделях-3
- 21 августа 2019, 13:49
- |
Устойчивые долгосрочные модели
В предыдущих частях (часть 1, часть 2) мы рассмотрели построение композитных систем оценок ценных бумаг, построенных при помощи распространённых средств машинного обучения (Bag/Boost методы). Однако, такой подход, несмотря на все свои преимущества (скорость, точность) имеет ряд больших недостатков – отсутствие универсальности моделей в результате проблем «переобучения» (точной настройки на определённые типы рынков и временные интервалы) и сложность интерпретации полученных композиций.
В результате решения этих проблем мы разработали базовую модель на основе наших представлений о стохастических дифференциальных уравнениях с квантовыми скачками, образующих улыбку волатильности. Эта макромодель получила в наших исследованиях наиболее полную микроскопическую интерпретацию.
( Читать дальше )
Блог им. Kot_Begemot |Стоимостные оценки портфельных инвестиций и двойственная природа стоимости ценных бумаг
- 08 июля 2019, 00:14
- |
Классическая финансовая математика рассматривает акцию как бесконечный поток нарастающих платежей или как бесконечную облигацию с нарастающим купоном. И, в этом смысле, акция имеет только одну, финансовую (портфельную) стоимость, определяемую исключительно будущим потоком платежей которые она принесёт своему собственнику. Но помимо своей финансовой стоимости, акция обладает ещё и прямой стоимостью — той ценой, которую готовы заплатить прямые инвесторы ради получения контрольного пакета.
Модель Гордона
Исходя из предпосылки постоянного темпа роста дивидендов, правил дисконтирования потоков платежей, и суммы геометрической прогрессии получаем :

Однако, данная методика не может служить действительным финансовым оценкам по той простой причине, что уже для самых простых объектов (таких как недвижимость), рентные платежи которых растут быстрее ставки рефинансирования (g>k) она даёт априорно неверный результат — бесконечную или отрицательную текущую стоимость.
( Читать дальше )
Блог им. Kot_Begemot |Большой секрет маленькой компании.
- 21 июня 2019, 23:37
- |
Ответ для SergeyJu:
Мы — маленькая инвестиционно-консалтинговая компания, вот уже 78 лет занимающаяся вложениями в фондовый рынок США. Все эти годы мы используем простую и очень понятную стратегию — мы покупаем только «прозрачные» акции в расчете получить «среднюю» доходность по рынку. Мы не читаем книг о том, как сделать из 5 долларов 50 миллиардов, случайно подписанных именем У.Баффета, и не играем в рулетку. Это простое правило позволяет нам получать портфели лучшие подавляющего большинства профессиональных управляющих США и, возможно, даже лучшие самого У.Баффета.
Мы не покупаем акции прямых инвестиций — ценность таких акций определяется только местом в совете директоров и сопутствующей внутренней кухней компаний. Мы не покупаем акции у инсайдеров — инсайдеры никогда не дадут войти в рынок по хорошей цене. Мы не покупаем акции у компаний в расчете на их порядочность и честность их аудиторов. Правильнее сказать, что мы
( Читать дальше )
Блог им. Kot_Begemot |Портфельная оптимизация как бустинг на «слабых» моделях
- 29 апреля 2019, 22:09
- |
Часть 2.
В прошлой части мы подбирали такую комбинацию статистических оценок динамики акций, которая давала нам возможность стабильно выбирать портфель акций лучше среднерыночного, с показателем Шарпа на 26% выше индексного.
Мы также пробовали составлять портфель из портфелей и портфель на основе портфеля оценок, но в силу высокой линейной зависимости оценок и полученных на них портфелей друг от друга Bagging ожидаемо не дал никакого результата.
Тем не менее, этот важный этап подготовительных работ – построение портфеля (или композиции портфелей) на простых, статистических оценках дал нам некоторую отправную точку, относительно которой мы будем рассматривать эффективность всех наших последующих нововведений.
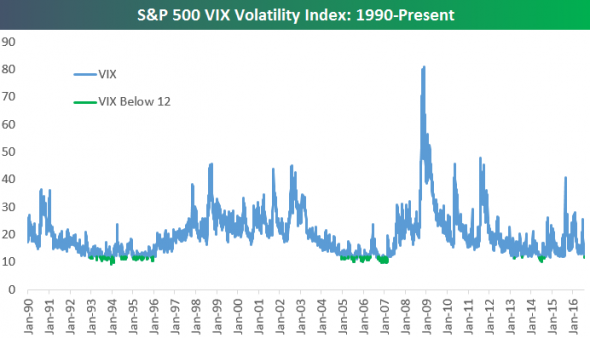
Рис. 6. Иллюстрация динамики волатильности акций США, входящих в состав индекса S&P 500.
Основную проблему стандартных методов мы видим в том, что они разработаны для стационарных стохастических процессов, в то время как любые финансовые (а зачастую природные, биологические и др.), временные ряды имеют нестационарную природу. Так, например, широко известно, что логарифмическое изменение стоимости акций является нестационарным процессом со склонностью к консолидации (кластеризации) волатильности.
( Читать дальше )
Блог им. Kot_Begemot |Портфельная оптимизация как бустинг на «слабых» моделях
- 09 апреля 2019, 23:20
- |
Часть 1.
Традиционно считается, что задача портфельной оптимизации, или задача Марковица, представляет собой некоторую самостоятельную задачу выбора такого портфеля активов, который обладал бы максимальной доходностью при минимальных рисках.
Прим. В качестве актива могут выступать ценные бумаги (акции), их производные (опционы) или торговые системы.
Решение задачи состоит из двух этапов:
- Прогноз доходности и ковариации активов в будущих периодах – то есть построение некоторого набора «слабых» прогностических моделей.
- Составление оптимального портфеля в соответствии с некоторой целевой функцией, и ранее полученными оценками. То есть построение такой композиции «слабых» моделей, которая обладала бы наибольшей прогностической силой.
Почему мы используем аналогию портфельной оптимизации с методами машинного обучения — Bag, Boost?! Потому что в действительности (и мы это продемонстрируем) нам абсолютно не важно, насколько хорошо динамику наших временных рядов прогнозируют «слабые» модели – нам важно только то, чтобы ошибки прогнозов наших моделей взаимно компенсировали бы друг друга в некотором интегральном смысле. Иными словами – в случае бустинга – ошибка прогноза линейной композиции была бы минимальной, а в случае портфельной оптимизации – была бы минимальной ошибка прогноза нелинейной композиции (то есть самого портфеля).
( Читать дальше )
- bitcoin
- brent
- eurusd
- forex
- gbpusd
- gold
- imoex
- ipo
- nasdaq
- nyse
- rts
- s&p500
- si
- usdrub
- wti
- акции
- алготрейдинг
- алроса
- аналитика
- аэрофлот
- банки
- биржа
- биткоин
- брокеры
- валюта
- вдо
- волновой анализ
- волны эллиотта
- вопрос
- втб
- газ
- газпром
- гмк норникель
- дивиденды
- доллар
- доллар рубль
- евро
- золото
- инвестиции
- индекс мб
- инфляция
- китай
- кризис
- криптовалюта
- лидеры роста и падения ммвб
- лукойл
- магнит
- ммвб
- мобильный пост
- мосбиржа
- московская биржа
- мтс
- нефть
- новатэк
- новости
- обзор рынка
- облигации
- опрос
- опционы
- отчеты мсфо
- офз
- оффтоп
- прогноз
- прогноз по акциям
- раскрытие информации
- ри
- роснефть
- россия
- ртс
- рубль
- рынки
- рынок
- санкции
- сбер
- сбербанк
- северсталь
- си
- сигналы
- смартлаб
- сущфакты
- сша
- технический анализ
- торговля
- торговые роботы
- торговые сигналы
- трейдер
- трейдинг
- украина
- фондовый рынок
- форекс
- фрс
- фьючерс
- фьючерс mix
- фьючерс ртс
- фьючерсы
- цб
- цб рф
- экономика
- юмор
- яндекс


















