SMART-LAB
Новый дизайн
Мы делаем деньги на бирже
Блог им. Kot_Begemot
Обобщённый подход к диверсификации рисков
- 28 августа 2019, 04:47
- |
Дополнение к серии «Портфельная оптимизация как бустинг на слабых моделях»
Результаты оценки любых случайных величин представляют из себя случайную величину. Не исключением здесь будут оценки ковариации.
Особенно сильно эффект неточности полученных оценок (случайности статистик) будет проявляться в портфелях, составленных из большого количества ценных бумаг — большего или сопоставимого количеству располагаемых наблюдений. И, поскольку, в некотором приближении задача портфельного инвестирования сводится к поиску двух максимально независимых активов из множества:
)
где R — коэффициент взаимной корреляции — её решение, естественным образом, будет располагаться в области максимально отрицательной статистической ошибки.
Иными словами, вследствие нелинейности самой задачи, ошибки в определении статистической взаимосвязи различных активов не уничтожаются суммированием( как это происходит при подсчёте средних), а, наоборот, усиливаются функцией min / max и приводят к абсолютно непредсказуемым, хаотичным результатам. Что, в свою очередь, означает не только не-оптимальные инвестиционные решения, но и большой объём «паразитного» оборота, повторяющего случайные блуждания портфеля, требующего повышенной ликвидности и разоряющего инвестора комиссиями биржи.
Для решения этих нелинейных проблем возможно использовать простые линейные алгоритмы, позаимствованные из методов статистической регрессии и известные как регуляризация (Тихонова, Лассо и пр.). Смысл этих методов состоит в том, чтобы перевести задачу из области нелинейности, связанной с поиском минимума корреляций, в некоторую область линейности, умышленно стимулировав широкодиверсифицированные инвестиции по всему рынку (без оглядки на корреляцию). Достигается это путём регуляризации или усадки матриц :
Cov_{basis})
где — Cov — ковариационная матрица используемая в задаче, Cov(sample) — выборочная ковариация, Cov(basis) — базисная ковариация, ламбда — параметр регуляризации, подбираемый бэк-тестом или выбираемый на каждом шаге исходя из общих характеристик матриц.
Видно, что при ламбда = 0, задача вырождается и приобретает характер задачи в некоторых априорных предположениях о характере взаимосвязи активов, заданных матрицей Cov(basis).
Этими априорными предположениями (базисом ковариации) могут выступать :
Забегая вперёд, отметим, что, в целом, результаты наших испытаний по этим методам соответствуют результатам сторонних авторов.
Второй подход, предложенный Р.Энглом (Theoretical and empirical properties of dynamic conditional correlation multivariate GARCH,
2001), заключается использовании динамических моделей корреляций (DCC) c использованием различных сглаживающих фильтров (например, фильтра Калмана или скользящей средней). В этом подходе используемая ковариационная матрица рассчитывается как:
Cov_{basis})
Это обобщённое уравнение совмещает в себе оба подхода — при бетта = 1/n и альфа+бетта =1, оно вырождается в уравнение усадки матриц, рассмотренное ранее, а при других значениях дополняет усадку фильтром Калмана ( в зависимости от соотношений альфа и бетта) и динамической моделью ковариации, зависящей от коэффициентов вектора бетта.
В качестве исходных данных для OOS теста моделей мы взяли фондовый рынок США, представленный 64 активами за период с 08.09.11 до 11.09.18. В качестве базовой модели оценки доходности — математическое ожидание IS выборки, рисков — модель на основе Bipower Variation. То есть самый простой и из всех возможных методов. Период наблюдений — 120 дней, минимальный из всех эффективных периодов, период инвестирования — 60 дней.
Апостериорный анализ возможностей портфельного инвестирования утверждает, что на выбранном интервале времени достижимы портфели с годовым коэффициентом Шарпа 1.32, в то же время базовая модель без преобразования ковариационных матриц достигает уровня качества не более чем 0.95.
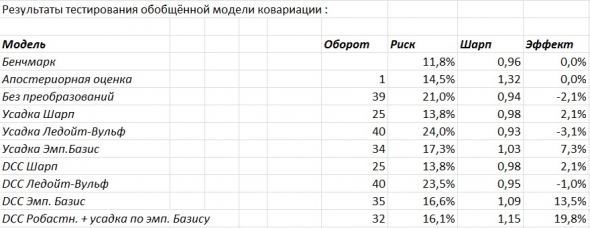
Таблица результатов тестов.
Из таблицы видно, что DCC (dynamic conditional covariation) модели в среднем выигрывают у CCC (constant conditional covariation) моделей. При этом стандартные процедуры усадки работают слабо удовлетворительно и почти не имеют эффекта. Модель Шарпа, при этом, превосходит модель Ледойт-Вульфа, вероятно из-за некоторой, присущей ей дискретности, связанной с не завышением ковариаций слабо коррелированных активов и слабым снижением ковариации сильно коррелированных активов. Устранить этот недостаток Ледойт-Вульф модели с сохранением всех её преимуществ (в качестве априорного предположения вводится ненулевая корреляция, что лучше соответствует действительности) позволяет более сложная факторная модель (Principal Component Analysis), разделяющая активы на группы слабо и сильно коррелированных с текущими движущими рынок факторами.
- Обобщённая проблема
Результаты оценки любых случайных величин представляют из себя случайную величину. Не исключением здесь будут оценки ковариации.
Особенно сильно эффект неточности полученных оценок (случайности статистик) будет проявляться в портфелях, составленных из большого количества ценных бумаг — большего или сопоставимого количеству располагаемых наблюдений. И, поскольку, в некотором приближении задача портфельного инвестирования сводится к поиску двух максимально независимых активов из множества:
где R — коэффициент взаимной корреляции — её решение, естественным образом, будет располагаться в области максимально отрицательной статистической ошибки.
Иными словами, вследствие нелинейности самой задачи, ошибки в определении статистической взаимосвязи различных активов не уничтожаются суммированием( как это происходит при подсчёте средних), а, наоборот, усиливаются функцией min / max и приводят к абсолютно непредсказуемым, хаотичным результатам. Что, в свою очередь, означает не только не-оптимальные инвестиционные решения, но и большой объём «паразитного» оборота, повторяющего случайные блуждания портфеля, требующего повышенной ликвидности и разоряющего инвестора комиссиями биржи.
- Усадка ковариационной матрицы (Shrinkage)
Для решения этих нелинейных проблем возможно использовать простые линейные алгоритмы, позаимствованные из методов статистической регрессии и известные как регуляризация (Тихонова, Лассо и пр.). Смысл этих методов состоит в том, чтобы перевести задачу из области нелинейности, связанной с поиском минимума корреляций, в некоторую область линейности, умышленно стимулировав широкодиверсифицированные инвестиции по всему рынку (без оглядки на корреляцию). Достигается это путём регуляризации или усадки матриц :
где — Cov — ковариационная матрица используемая в задаче, Cov(sample) — выборочная ковариация, Cov(basis) — базисная ковариация, ламбда — параметр регуляризации, подбираемый бэк-тестом или выбираемый на каждом шаге исходя из общих характеристик матриц.
Видно, что при ламбда = 0, задача вырождается и приобретает характер задачи в некоторых априорных предположениях о характере взаимосвязи активов, заданных матрицей Cov(basis).
Этими априорными предположениями (базисом ковариации) могут выступать :
- Предположение о нулевой корреляции активов (Sharpe,1963)
- Предположение о некотором общем уровне взаимосвязи для всех активов (Ledoit & Wolf,2003)
- Отсутствие каких либо априорных предположений и использование эмпирического базиса в целях усадки (PCA, задача настоящей работы)
Забегая вперёд, отметим, что, в целом, результаты наших испытаний по этим методам соответствуют результатам сторонних авторов.
- Динамические модели условных корреляций и функции сглаживания
Второй подход, предложенный Р.Энглом (Theoretical and empirical properties of dynamic conditional correlation multivariate GARCH,
2001), заключается использовании динамических моделей корреляций (DCC) c использованием различных сглаживающих фильтров (например, фильтра Калмана или скользящей средней). В этом подходе используемая ковариационная матрица рассчитывается как:
Это обобщённое уравнение совмещает в себе оба подхода — при бетта = 1/n и альфа+бетта =1, оно вырождается в уравнение усадки матриц, рассмотренное ранее, а при других значениях дополняет усадку фильтром Калмана ( в зависимости от соотношений альфа и бетта) и динамической моделью ковариации, зависящей от коэффициентов вектора бетта.
- Оценка качества моделей при решении тестовой проблемы
В качестве исходных данных для OOS теста моделей мы взяли фондовый рынок США, представленный 64 активами за период с 08.09.11 до 11.09.18. В качестве базовой модели оценки доходности — математическое ожидание IS выборки, рисков — модель на основе Bipower Variation. То есть самый простой и из всех возможных методов. Период наблюдений — 120 дней, минимальный из всех эффективных периодов, период инвестирования — 60 дней.
Апостериорный анализ возможностей портфельного инвестирования утверждает, что на выбранном интервале времени достижимы портфели с годовым коэффициентом Шарпа 1.32, в то же время базовая модель без преобразования ковариационных матриц достигает уровня качества не более чем 0.95.

Таблица результатов тестов.
Из таблицы видно, что DCC (dynamic conditional covariation) модели в среднем выигрывают у CCC (constant conditional covariation) моделей. При этом стандартные процедуры усадки работают слабо удовлетворительно и почти не имеют эффекта. Модель Шарпа, при этом, превосходит модель Ледойт-Вульфа, вероятно из-за некоторой, присущей ей дискретности, связанной с не завышением ковариаций слабо коррелированных активов и слабым снижением ковариации сильно коррелированных активов. Устранить этот недостаток Ледойт-Вульф модели с сохранением всех её преимуществ (в качестве априорного предположения вводится ненулевая корреляция, что лучше соответствует действительности) позволяет более сложная факторная модель (Principal Component Analysis), разделяющая активы на группы слабо и сильно коррелированных с текущими движущими рынок факторами.
2.1К |
Читайте на SMART-LAB:
Оперативная заметка с полей облигационной конференции для клиентов Mozgovik Research
Доброго дня, уважаемые читатели Mozgovik Research.
Для вас хотел коротко и оперативно поделиться основными идеями, которые успел услышать на...
17:22
теги блога Kot_Begemot
- API
- cpp
- FORTS
- LUA
- Matlab
- NASDAQ
- open source
- Quik Lua
- S&P
- S&P500
- S&P500 фьючерс
- Vanguard Group
- VIX
- акции
- акции США
- алгоритмы
- алготрейдинг
- анализ временных рядов
- баффет
- волатильность
- Гордон
- доверительное управление
- долги
- игры
- инвестиции
- индекc
- интеграция
- искусственный интеллект
- Келли
- Книги
- книги о трейдинге
- корреляция
- кризис
- криптовалюта
- лудомания
- Марковиц
- матлаб
- машинное обучение
- ММВБ Акции
- наука
- нейронные сети
- облигации
- одураченные случайностью
- оптимизация
- оптимизация торговых систем
- опционы
- оффтоп
- оционы
- памм счета инвестиции
- паника
- пирамида
- ПИФы
- портфели
- Портфель
- портфельное инвестирование
- пузыри
- раздача
- рецензия
- Риски
- рэнкинг мосбиржи
- Сбербанк
- спекуляции
- статистика
- стоимостное инвестирование
- талеб
- теги не нужны
- теория игр
- торговая система
- торговые роботы
- трейдинг
- улыбка волатильности
- управляющая компания
- финанализ
- фундаментальный анализ
- фьючерс ртс
- Шарп
- шутка
- Экономика





















К самой же ков. матрице нужно применять другие алгоритмы, например КNN, раскладывая активы в коррелированные и не-коррелированные группы. То есть, своего рода, бинаризация ковариационной матрицы.
Как использовать SSA в целях разложения самой ков. матрицы я на сегодняшний день не представляю.
SVD разложение аппроксимирует строки матрицы. Если вы применяете его к траекторной матрице, как положено, то получаете мощность некоторого сигнала и реакцию каждой акции на этот сигнал (например цены на нефть).
Как только вы применяете SVD к ковариационной матрице, то получаете глупость, так как ковариационная матрица не имеет некоторой строковой структуры.
Представьте, что у вас в качестве актива 1 — нефть, которая определяет цену 2 актива — акций Роснефти. Корр.матрица, соответственно: [ 1, 0.5; 0.5, 1 ]; Всего одна Г.К + 1 шумовая часть.
А теперь разложим эту матрицу по SVD и получим две ортогональных Г.К. — [0.7, 0.7] и [-0.7, 0.7].
Итого, восстановленная матрица по 1-ой Г.К. будет выглядеть так :
[ 0.75, 0.75; 0.75, 0.75 ]
То есть совершенно неверное решение! (Не то, которое предполагалось).
А если бы вы повернули Корр.матрицу на 45 градусов, чтобы в ней появилась построчная структура, то да — вы бы получили то, что хотели, а именно 1 Г.К без шума.
Ясно, что идеального совпадения не будет, также ясно, что ЛЮБАЯ регуляризация искажает матрицу.
P.S. У Вас, кстати, матрица не ковариационная, а корреляционная.
Возникновение улыбки волатильности в данном случае может быть просто следствием дисбаланса покупателей и продавцов, использующих в своих оценках формулу Б-Ш и, как следствие, саму улыбку.
Что касается Марковица, то всё опять же зависит от задачи. Если вы — свободный частный трейдер — то… побить индекс портфелем Марковица вам не удастся. И первые мои опыты показывали именно это. Если вы управляющий портфелем крупного банка, у которого на балансе акции Газпрома на 2 трлн. рублей в качестве прямых инвестиций и в вашу задачу входит только диверсификация рисков этой, конкретной прямой инвестиции (с учётом доходности) — то Марковиц вам вполне эту задачу решит и сделает это лучшим образом.
Это совершенно не меняет дело.
1. Оценки прошлой доходности не обязательно должны использоваться в качестве прогноза. Я тестировал несколько фундаментальных стратегий и неожиданно получил пренеприятную проблему — сильный (неконтролируемый, слабоконтролируемый) рост рисков.
Иными словами, Марковиц на прошлых доходностях это только частный случай портфельной оптимизации.
2. Вопрос не в том, что рынок нестационарен, вопрос в том — мешает ли эта нестационарность конкретным методам. Если рынок, например, состоит из интервально-стационарных процессов с некоторым временем жизни (экспоненциально распределённым), то это уже позволит работать на нём разнообразным трендовым стратегиям в определённом интервале окон.
Если на рынке наблюдается GARCH / ARCH, то это тоже не нанесет большого ущерба портфелям Марковица — качество работы резко снизит, но правильное решение в неправильное не превратит.
Собственно, в этом вся и закавыка — проплыть океан нестационарных айсбергов, не столкнувшись ни с одним из них.
Да, CAPM модель изначально строится на допущении, что портфель по Марковицу и есть рыночный портфель. А так же на допущении того, что все инвесторы рациональны и имеют именно этот рыночный портфель. И потому уже ценность актива для них определяется с точки зрения альфа и бетта коэффициента, то есть с точки зрения способности конкретного актива диверсифицировать именно рыночный портфель (а не собственный портфель инвестора, если бы этот портфель был отличен от рыночного).
Тем не менее, это не означает, что невозможно на малых капиталах собрать портфель лучше. Более того, это даже не означает, что на крупных капиталах невозможно собрать портфель лучше, так как рациональность инвесторов и преследуемые ими цели (например, прямые инвестиции) могут быть различны, что приводит к некоторым отклонениям от CAPM.
Самое смешное, что сама CAPM в собственных предположениях не должна допускать недооценённости/переоценённости активов, так как предполагает, что рынок эффективен всегда. Но у инвесторов, как минимум существуют и собственные прогнозы относительно рынка, что создаёт предпосылки для переоценки/недооценки активов по SML, и, соответственно, опровергает изначальные положения модели CAPM.
1. Не совсем понятна задача t-testa.
Разница, безусловно есть и очень сильная. Шарп давит доходность превращая портфель в индекс (16%). Вульф оставляет высокую доходность, но не диверсифицирует риски (23%), PCA сохраняет доходность (около 20%) с хорошим подавлением дисперсии. Поэтому да — значимая разница есть.
2. Ни на каком. Для того, чтобы получить «честный OOS» использую только непараметрические фильтры. Параметр длинны выборки не подбирался. За исключением того, что был выбран минимальный (самый тяжёлый для прогнозирования) из всех статистически значимых (эффективных) периодов. На периодах в 60 дней и менее, в силу случайности динамики ВР, уже невозможно выделить среднюю, ковариацию и т.д.
3. Начинал с BrokenStick, но пришлось её ослабить, так как «сломанная трость» выделяла только 1 Г.К. после… некоторой модернизации в среднем PCA оставило 4 компоненты. (на глаз я бы оставил только 3).
Это самый простой в реализации автомат. Для проверки качества методов — вполне достаточно.
Это всегда приветствуется!
1.
Сейчас я вам ничего не отвечу, но за подсказку — спасибо.
2.
Какими только извращениями на этом пути я не занимался. Результат — так себе. В итоге пришёл к выводу, что квадратичная оценка ковариаций одна из лучших. Регуляризую, естественно, корреляционную матрицу, а потом совершаю обратный пересчёт.
Предположим, что вы имеете две модели с доходностью 10% и 10.01% — разница не значимая, но какую модель вы выберете?
В лучшем случае, можно выбрать комбинацию из двух. Но при этом ответить на вопрос какая модель однозначно лучше вы не можете. Единственное, что вы можете указать, что вероятность того, что модель с бОльшей доходностью лучше — больше, вот и всё.
Поэтому применять t-test для того, чтобы найти существенную разницу между моделями не вижу особого смысла, потому как построить две модели (с разницей в 1 метод) с явным стат. преимуществом как-то не получается. За 5-10 модернизаций появляется ощутимое различие (раза в 2 по Шарпу) и тут уже можно о чём-то говорить, но применительно к одному дополнению типа Shrinkage — нет.
Вот, например, то же DCC не работает с Шарпом (по понятным причинам) и не очень работает в голом виде (на грани t-testa, на глаз), но совместно с другими методами — тем же PCA — работает намного лучше. А так вы хорошую правку отбросите в самом начале, если будете всё по тестам проверять.
Поясню в чём проблема :
Исходная корр. матрица по 64 активам за 7 лет.
Восстановленная корр. матрица по 0 Г.К.
Восстановленная корр. матрица по 1 Г.К.
Ни один ваш метод, работающий сразу с корр/ков. матрицей этого не даст.
Было бы интересно.
понятно
главу про кнопку «Бабло» можно не ждать
И неожиданно понял, что чистая ков. матрица должна быть построково структурирована (как у меня на последней картинке). А ещё пол дня назад был уверен в обратном...
[0,0,0,1,1,0] что означает, что 4 и 5 -ый активы из 6 ходят парой с некоторым управляющим воздействием (Г.К.).
Соответственно, на другой строке, коррелированной с тем же управляющим воздействием должна получаться эта же структура — [0,0,0,1,1,0].
Исходя из этого, все (в том числе и мои, построенные на сингулярном разложении рядов) PCA корр. матрицы будут с виду напоминать «набор вертикальных линий» (если совсем грубо), повторяя сами себя от строки к строке. ( что и получается. на моих картинках).
Изначально, поскольку PCA это всего лишь — линейный, сглаживающий фильтр строк и в условиях отсутствия представлений о «правильном» виде матрицы ковариации, было решено использовать PCA для самих рядов. Потому что для рядов должно было выполняться это условие построковой структуры из предположений о стационарном отклике на некоторый невидимый, управляющий фактор. То есть для рядов линейная модель была понятна, а для матриц — нет. Отсюда и непонимание.
Зачем Вы используете построчный фильтр я не понял. Или Вы используете SVDразложение прямоугольной матрицы, не сворачивая её в ковариационную?
Любое PCА и есть построчный фильтр. Если вам нужен какой-нибудь другой фильтр, например диагональный или выискивающий закономерности в некоторых разбросанных по плоскости (матрице) точках — PCA уже будет не применим. Я поэтому сразу сказал (неверно), что нужно использовать для ков./кор. матриц KNN или что-то подобное, отвязанное от строк.
Например, закономерность вида :
0,1,0
0,0,1
1,0,0
требующую разложения в 1 компоненту вы уже через PCA не разложите (в данном случае наблюдается диагональный сдвиг единиц). А через тот же KNN вполне себе найдете кластер.
Так, результатом работы PCA будет строка (собственный вектор)
А KNN — матрица (то есть некоторая двумерная структура).
И поэтому PCA соберёт восстановленную матрицу из последовательных одинаковых строк, но с разной амплитудой, а KNN как суперпозицию матриц с разной амплитудой.
Интересно, Вы сами этот эффект обнаружили, или где-то прочли.