Кому улыбается волатильность?

Волатильность, как хороший продавец — всегда улыбается своему покупателю. Шутка с долей шутки.


Предположим, что в качестве фундаментального сигнала (событийный ряд) у нас выступает некоторая случайная величина, обладающая следующими «катастрофическими» свойствами:

1. Существует некоторая средняя мощность событий во времени.
2. Если не произошло малого события, то, вероятно, произойдет большое, если не произошло большого, то, вероятно, произойдёт катастрофическое, если не произошло катастрофического — произойдёт ещё более катастрофическое.  Как при землетрясениях и лавинах.
3. Сила события не зависит от уже произошедшей силы события (невозможность скальпинга), то есть отсутствуют ограничения и эффекты памяти для последующего роста мощности события, а  функция плотности распределения моментальной мощности в каждой своей точке имеет самоподобную природу. 



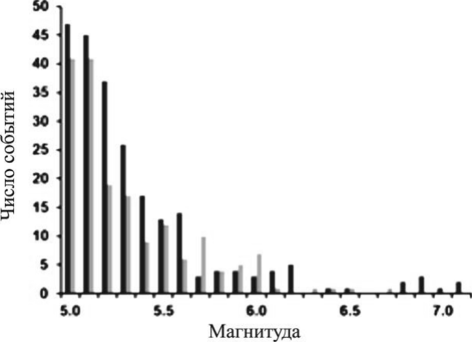
Рис1. Распределение землятресений с магнитудой более 5 США, 1973-2010 год.


Надо отметить, что в математике существует достаточное разнообразие моделей для описания подобного рода статистик — это и мерцательные эффекты, и фрактальные множества и прочее, прочее, прочее ( в зависимости от приложения) Мы обычно пользуемся иерархическими моделями, предполагающими взаимосвязанную структуру множества субъектов/факторов по единому правилу или, применительно к финансовым временным рядам,- модели финансовых пирамид, кризисов или самоорганизующихся паник финансовых рынков. 


Соответственно этой вводной эффективный рынок должен один в один повторять событийный ряд, не растягивая эти события во времени из-за задержек распространения и обработки информации и не давая возможности совершения временного арбитража (торговля трендов).  Распределение волатильности на таком рынке будет иметь весьма и весьма «тяжёлые хвосты» точку разрыва производной в медиане (острый пик).

Абсолютно неэффективный рынок будет, напротив, иметь распределение Гаусса, поддерживающего постоянную волатильность во времени независимо от катастрофического событийного фона, а полу-эффективный рынок — будет обладать некоторыми промежуточными свойствами, то реагируя на события относительно эффективно, то и вовсе  не замечая их (при долгосрочном схождении равновесной фундаментальной и спот цены). 

Промоделируем 50-летний тренд на трёх рынках (с математическим ожиданием цены актива 300 логарифмических единиц):



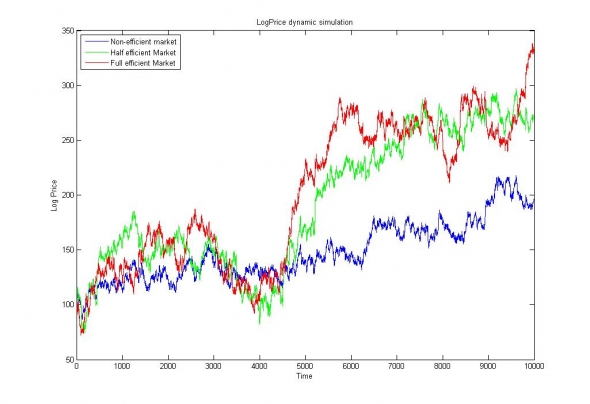
Рис.2. Симуляция логарифмической динамики цены актива с одинаковой долгосрочной волатильностью и одинаковым математическим ожиданием. Красная кривая — эффективная динамика актива, зелёная и синяя — полу-эффективная динамика и неэффективная динамика.

По общему виду графиков можно обратить внимание на неустойчивость волатильности трендов, обладающих «тяжёлыми хвостами».


Рассмотрим отдельно полученное полу-эффективное распределение, случайным образом принимающее форму эффективного «катастрофического» и неэффективного Гауссового:


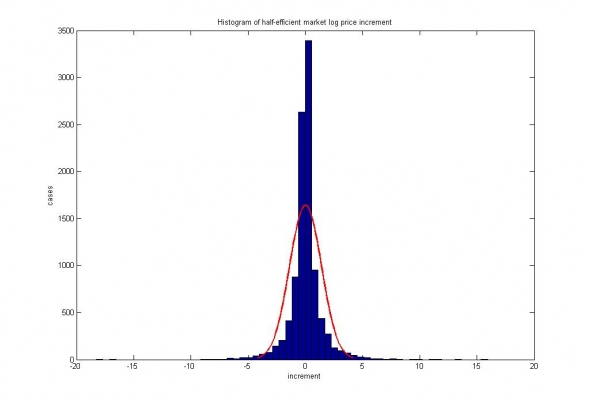
Рис 3. Полу-катастрофическое распределение волатильности, характерное для полу-эффективного рынка, выраженное в логарифмических ценах.


Теперь предположим, что та же динамика катастроф свойственна не только внутридневной волатильности, но и долгосрочной волатильности. Это предположение позволяет нам перенести экспоненциальную составляющую распределения приращений стоимости на вероятностное распределение абсолютной стоимости актива: 


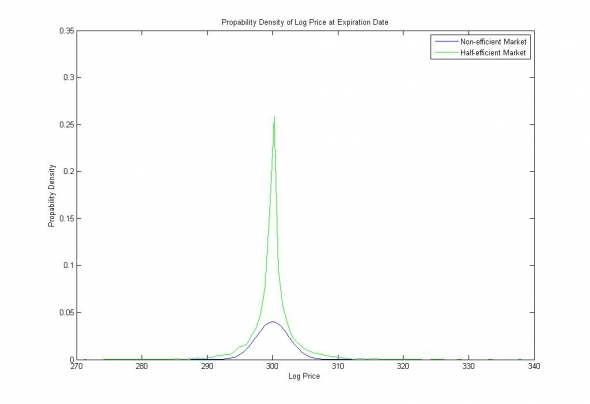
Рис 4. Плотность распределения логарифмической цены актива в будущем. Синяя кривая соответствует модели Блэка-Шоулза неэффективного рынка, зелёная кривая — модели случайного блуждания с полу-катастрофической волатильностью. Разница амплитуд обусловлена разницей числа статистических интервалов.


Теперь рассчитаем численно цену колл опционов для обоих типов распределений:


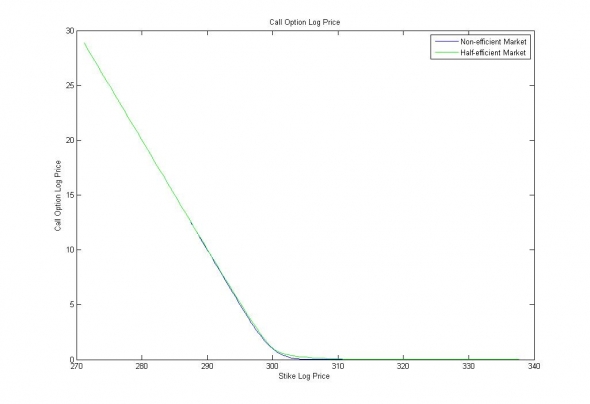
Рис 5. Логарифмические цены опционов для процессов с постоянной и полу-катастрофической волатильностью.


И пересчитаем полученную цену call опционов в «Implied Volatility», то есть в аналогичную стационарную волатильность:


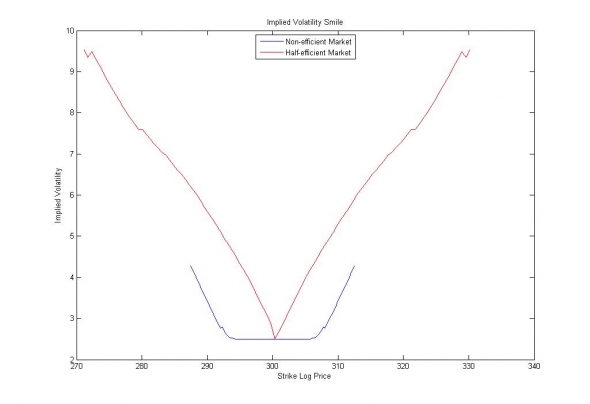
Рис 6. Улыбка волатильности для процесса с постоянной волатильностью (синяя кривая) и процесса с катастрофической волатильностью. Хвосты синей улыбки обусловлены ошибками численного интегрирования в пределах  страйков 3-5 сигма)

Отчётливо видно, что улыбка волатильности процесса с «катастрофическим риском»  имеет отрицательную вторую производную (выпуклость ветви вверх) и обратную выпуклость  в области близких к трендовой составляющей страйков. В то же время «ожидаемая волатильность» процесса со стационарной волатильностью, как и полагается, в первом приближении равна константе. 

Однако, в процессе моделирования мы сделали одно необоснованное предположение, противоречащее условиям центральной предельной теоремы теории вероятностей в области большого числа событий. Так, например, даже при сильной склонности к долгосрочным трендам или иным  регрессионным зависимостям (цепи Маркова и пр.), результирующее распределение суммы большого числа периодов остаётся распределением нормальным или близким к таковому. Но если предположить о существовании редких, чуть ли не единичных артефактов, появляющихся малое число раз на рассматриваем временном промежутке (то есть предложить вероятность возникновения единичного кризиса), то в результирующем распределении интегрального результата удаётся сохранить «тяжёлые хвосты», как отражение несбалансированной суммы этих кризисов.

При этом, что интересно — как и в случае с внутридневной волатильностью, содержащей в себе достаточное количество объёмов, чтобы быть неразличимой от распределения Гаусса, но содержащей «толстые хвосты» в качестве отражения влияния редких событий, так и в случае волатильности больших периодов, мы наблюдаем некоторое слабое самоподобие.

Таким образом волатильность ещё улыбается и артефактам — редким финансовым кризисам и паникам больших амплитуд.