Блог им. Zmey56 |Анализ и визуализация данных в финансах — анализ ETF с использованием Python
- 18 сентября 2021, 00:55
- |
1. О данных
Для анализа будем использовать данные ETF c базовой валютой USD: FXCN, FXRL, FXIT, FXUS и FXRU. Временной ряд рассмотрим за три года с 2018 по 2020 года. Само исследование проведем в Google Colaboratory.
Как обычно в начале импортируем все необходимые библиотеки для дальнейшей работы.
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from google.colab import files
import warnings
warnings.filterwarnings("ignore")Сначала необходимо получить данные. Есть несколько способов. Мы воспользовались — взяли их с Finam в формате csv. Дальше написал функцию для обработки полученных данных и при помощи concat свел их в один датафрейм.def changeDF(df): df['date'] = pd.to_datetime(df['<DATE>'].astype(str), dayfirst=True) name =[x for x in globals() if globals()[x] is df][0] df = df.drop(['<DATE>','<TIME>', '<OPEN>', '<HIGH>', '<LOW>'], axis=1) df = df.set_index(['date']) df.columns = [name+'_cl', name + '_vol'] return df fxgd_change = changeDF(fxgd) fxrl_change = changeDF(fxrl) fxit_change = changeDF(fxit) fxus_change = changeDF(fxus) fxru_change = changeDF(fxru) fxcn_change = changeDF(fxcn) etf = pd.concat([fxgd_change, fxrl_change, fxit_change, fxus_change, fxru_change, fxcn_change], axis=1) etf.head()В результате получили:
( Читать дальше )
- комментировать
- ★38
- Комментарии ( 13 )
Блог им. Zmey56 |Оптимизации портфеля с помощью Python и PyPortfolioOpt
- 11 мая 2021, 21:57
- |
Портфельная теория Марковица(далее ПТМ) (Modern portfolio theory) — разработанная Гарри Марковицем методика формирования инвестиционного портфеля, направленная на оптимальный выбор активов, исходя из требуемого соотношения доходность/риск. Сформулированные им в 1950-х годах идеи составляют основу современной портфельной теории.
Основные положения портфельной теории были сформулированы Гарри Марковицем при подготовке им докторской диссертации в 1950—1951 годах.
Рождением же портфельной теории Марковица считается опубликованная в «Финансовом журнале» в 1952 году статья «Выбор портфеля». В ней он впервые предложил математическую модель формирования оптимального портфеля и привёл методы построения портфелей при определённых условиях. Основная заслуга Марковица состояла в предложении вероятностной формализации понятий «доходность» и «риск», что позволило перевести задачу выбора оптимального портфеля на формальный математический язык. Надо отметить, что в годы создания теории Марковиц работал в RAND Corp., вместе с одним из основателей линейной и нелинейной оптимизации — Джорджем Данцигом и сам участвовал в решении указанных задач. Поэтому собственная теория, после необходимой формализации, хорошо ложилась в указанное русло.
( Читать дальше )
Блог им. Zmey56 |Использование API Fmp Cloud для отбора акций по дивидендам на Nasdaq с помощью Python
- 21 марта 2021, 20:02
- |
Акции с высокой дивидендной доходностью часто являются отличной инвестиционной стратегией для инвесторов, стремящихся получать приток денежных средств каждый год. В данной статье буден создан скрипт на Python для отбора их на бирже NASDAQ.
Что такое дивидендная доходность?Возьму определение из Википедии. Дивиде́ндная дохо́дность (англ. dividend yield) — это отношение величины годового дивиденда на акцию к цене акции. Данная величина выражается чаще всего в процентах.
Пример
При цене акции ОАО «Лукойл» 1124,37 рублей и дивиденде 28 рублей на акцию дивидендная доходность будет равна:
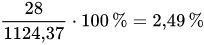
Так же необходимо обратить внимание, что многие растущие компании, такие как для примера Amazon и Yandex, не выплачивают дивиденды, поскольку они реинвестируют всю прибыль в развитие бизнеса. Поэтому дивидендная доходность для этих фирм будет равна нулю.
Расчет дивидендной доходности с помощью Python
( Читать дальше )
Блог им. Zmey56 |Использование метода Монте-Карло для создания портфеля
- 26 апреля 2020, 14:17
- |
Начинающие (да и не только) инвесторы часто задаются вопросом о том, как отобрать для себя идеальное соотношение активов входящих в портфель. Часто (или не очень, но знаю про двух точно) у некоторых брокеров эту функцию выполняет торговый робот. Но заложенные в них алгоритмы не раскрываются.
В этом посте будет рассмотрено то, как оптимизировать портфель при помощи Python и симуляции Монте Карло. Под оптимизацией портфеля понимается такое соотношение весов, которое будет удовлетворять одному из условий:
- Портфель с минимальным уровнем риском при желаемой доходности;
- Портфель с максимальной доходностью при установленном риске;
- Портфель с максимальным значением доходности
Для расчета возьмем девять акций, которые рекомендовал торговый робот одного из брокеров на начало января 2020 года и так же он устанавливал по ним оптимальные веса в портфеле: 'ATVI','BA','CNP','CMA', 'STZ','GPN','MPC','NEM' и 'PKI'. Для анализа будет взяты данные по акциям за последние три года.
#Загружаем библиотеки import pandas as pd import yfinance as yf import numpy as np import matplotlib.pyplot as plt # Получаем данные по акциям ticker = ['ATVI','BA','CNP','CMA', 'STZ','GPN','MPC','NEM', 'PKI'] stock = yf.download(ticker,'2017-01-01', '2019-01-31')
( Читать дальше )
Блог им. Zmey56 |Общий финансовый анализ на Python (Часть 3)
- 05 апреля 2020, 12:51
- |
После всех вычислений, приведенных в этой и этой публикациях, можно углубиться в статистический анализ и рассмотреть метод наименьших квадратов. Для этой цели используется библиотека statsmodels, которая позволяет пользователям исследовать данные, оценивать статистические модели и выполнять статистические тесты. За основу были взяты эта статья и эта статья. Само описание используемой функции на английском доступно по следующей ссылке.
Сначала немного теории:
О линейной регрессии
Линейная регрессия используется в качестве прогнозирующей модели, когда предполагается линейная зависимость между зависимой переменной (переменная, которую мы пытаемся предсказать) и независимой переменной (переменная и/или переменные, используемые для предсказания).
( Читать дальше )
Блог им. Zmey56 |Общий финансовый анализ на Python (Часть 2)
- 22 марта 2020, 13:48
- |
Скользящее окно(Moving Windows)
В заголовке я привел дословный перевод. Если кто меня поправит, и другой термин применяется — то спасибо.
Смысл скользящего окна– с каждым новым значением функция пересчитывается за заданный период времени. Этих функций большое количество. Для примера: rolling.mean(), rolling.std(), которые чаще всего и используют при анализе движения акций. rolling.mean() — это обычная скользящая средняя, которая сглаживает краткосрочные колебания и позволяет визуализировать общую тенденцию.
# Выделяю скорректированную цену закрытия adj_close_px = sber['Adj Close'] # Вычисляю скользящую среднию moving_avg = adj_close_px.rolling(window=40).mean() # Вывожу результат print(moving_avg[-10:])

Дальше построим график, чтоб лучше понять то, что получается в результате работы данной функции:
# Вычисление короткой скользящей средней sber['40'] = adj_close_px.rolling(window=40).mean() # Вычисление длинной скользящей средней sber['252'] = adj_close_px.rolling(window=252).mean() # Построение полученных значений sber[['Adj Close', '40', '252']].plot(figsize=(20,20)) plt.show()
( Читать дальше )
- bitcoin
- brent
- eurusd
- forex
- gbpusd
- gold
- imoex
- ipo
- nasdaq
- nyse
- rts
- s&p500
- si
- usdrub
- wti
- акции
- алготрейдинг
- алроса
- аналитика
- аэрофлот
- банки
- биржа
- биткоин
- брокеры
- валюта
- вдо
- волновой анализ
- волны эллиотта
- вопрос
- втб
- газ
- газпром
- гмк норникель
- дивиденды
- доллар
- доллар рубль
- евро
- золото
- инвестиции
- индекс мб
- инфляция
- китай
- кризис
- криптовалюта
- лукойл
- магнит
- ммвб
- мобильный пост
- мосбиржа
- московская биржа
- мтс
- натуральный газ
- нефть
- новатэк
- новости
- обзор рынка
- облигации
- опрос
- опционы
- отчеты мсфо
- офз
- оффтоп
- прогноз
- прогноз по акциям
- путин
- раскрытие информации
- ри
- роснефть
- россия
- ртс
- рубль
- рынки
- рынок
- санкции
- сбер
- сбербанк
- северсталь
- сигналы
- смартлаб
- сущфакты
- сша
- технический анализ
- торговля
- торговые роботы
- торговые сигналы
- трамп
- трейдинг
- украина
- фондовый рынок
- форекс
- фрс
- фьючерс
- фьючерс mix
- фьючерс ртс
- фьючерсы
- цб
- цб рф
- экономика
- юмор
- яндекс


















