Блог им. 3Qu |Нейросети и стопы.
- 04 мая 2023, 20:51
- |
Недавно, после продолжительного перерыва, вернулся к занятиям машинным обучением (МО) и даже написал по этому поводу топик — Все надоело или Deep Lerning (Глубокое Обучение). С тех пор даже прочитал ~150 страниц книги «Глубокое обучение...» Искренне полагал, что за эти 150 страниц что-то узнал. Ан, нет, на 151 странице автор объявил, что это все так — объяснения для тех, кто вообще ничего о МО не слышал и автор, оказывается, только приступает к изложению материала.) Но кое что узнать все же было можно, автор показал несколько экземлов построения нейросетей (НС), прменяемых для классификации и регрессии, из которых уже можно попробовать сделать что-то свое.
Ну, и почему бы эти знания о НС не попробовать применить для построения торговой системы (ТС). Не, это не то, что вы можете подумать, вовсе не Грааль на НС — это просто попытка встроить НС в уже готовую ТС как дополнительный функционал, не ухудшающий, но, возможно, улучшающий характеристики ТС. Решено было начать с небольшой модернизации стопа.
( Читать дальше )
- комментировать
- Комментарии ( 33 )
Блог им. 3Qu |Хотите попрогнозировать рыночные котировки? Нет проблем - вот код.
- 14 сентября 2021, 22:46
- |
import sqlite3 as sql
from scipy.stats import logistic
import math
import numpy as np
import numpy.random as rnd
import matplotlib.pyplot as plt
from sklearn.neural_network import MLPRegressor
sdata =[]
sql1= "select ticker, date, open, high, low, close, vol \
from Hist_1m where ticker_id=1 order by Date;"
con=sql.connect('C:/Users/ubase/Documents/StockDB/StockDB21.sqlite')
cur=con.cursor()
cur.execute(sql1)
sdata=cur.fetchall()
con.commit()
con.close()
Ldata = len(sdata)
N = 8000 # Количество сделок
ld = 5 #Продолжительность сделки
NNinterval = 20 # Количество входов NN
# Генерация случайных чисел
rng = rnd.default_rng()
rm=rng.integers(0, Ldata, N )
class Candle:
tr = 0
dt = 1
o = 2
h = 3
l = 4
c = 5
v = 6
cl = Candle
DataC =[sdata[i][cl.c] for i in range(0,Ldata)]
# sigmoid линейность до 0.5
def sigmoidnorm(x, alfa = 0.9, xmin = -1.3, xmax = 1.3):
return (xmax - xmin)*((1 / (1 + math.exp(-x*2.0*alfa))) - 1.0) + xmax
x = [0.002 * i - 3 for i in range(0,3000)]
y = [sigmoidnorm(x[i]) for i in range(len(x))]
plt.plot(x,y)
plt.grid()
plt.show()
# формируем сделки.
def DealsGenL(rm,ld):
#Lm = len(rm)
ix = []
x = []
pr = []
for i in range(0,N):
if rm[i] + ld < Ldata and rm[i] - NNinterval - 1 > 0:
delta = (sdata[rm[i]+ld][cl.c] - sdata[rm[i]][cl.c])/sdata[rm[i]+ld][cl.c]*100
x0 = [sigmoidnorm((sdata[rm[i] - j][cl.c] - sdata[rm[i]][cl.c])/sdata[rm[i]][cl.c]*100) \
for j in range(0, NNinterval)]
ix.append(rm[i])
x.append(x0)
pr.append(delta)
return ix, x, pr
Ix, X, Pr = DealsGenL(rm,ld)
Ib = 0
Ie = 100
plt.plot(X)
plt.legend()
plt.grid()
plt.show()
plt.plot(Pr, label = 'Prof')
plt.legend()
plt.grid()
plt.show()
regr = MLPRegressor(hidden_layer_sizes = [30,20,15,10,5], \
max_iter=500, activation = 'tanh')
regr.fit(X, Pr)
Out = regr.predict(X)
plt.plot(Pr, Out, '.')
plt.grid()
plt.show()И вот результат прогнозирования:( Читать дальше )
Блог им. 3Qu |Сравнение торговой системы на индикаторах и нейросети. Это как это?
- 01 сентября 2021, 21:28
- |
Не, конечно можно сравнить между собой две системы — одну на индикаторах, другую на нейросети — не вопрос. Но вопрос, что, если сделать такую же ТС как на нейросети (НС), но на индикаторах, а потом их сравнить?, лишен смысла.
Для тех кто не в танке. Что есть нейрон НС?
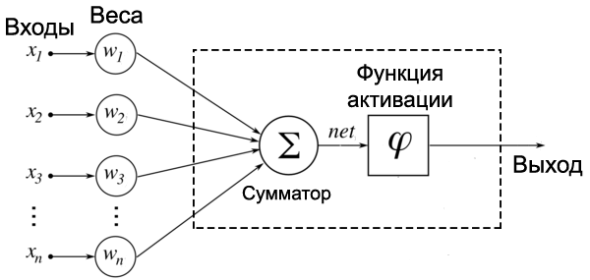
Всего лишь сумматор, на выходе которого прикреплена некая нелинейность, сигмоид, например.
Если подать на входы нейрона значения цены с интервалом Т (скажем, 1 минута), то на выходе сумматора получим значения нашего любимого индикатора WMA.
Допустим, таких нейронов во входном слое НС штук 20. Получается, что только один входной слой нашей НС уже содержит 20 различных индикаторов WMA.
Если слоев у нас несколько, то одна НС уже может иметь в своем составе сотенку-другую индикаторов WMA перемежающихся нелинейными элементами (скажу только, что нелинейные элементы там нужны).
Ну, и каким образом мы собираемся строить на индикаторах ТС аналогичную НС? Хотел бы я посмотреть на того героя, любителя индикаторов.)
Все тоже самое относится и к другим методам машинного обучения. Но, если что, то вперед за орденами, стройте.)
Это так, немного достало.)
Блог им. 3Qu |Нейросети в торговых системах. 1.
- 25 июня 2020, 22:59
- |
Вначале о грустном. Не понимая теорию нейросетей (НС) у вас вряд ли получится построить на ней ТС. Поэтому лучше для начала почитать теорию, например, Хайкин Саймон. «Нейронные сети. Полный курс». Книга уже достаточно старая и в ней нет новомодных веяний, но она дает базовые представления о НС.
И второе, мы будем далее для построения систем использовать пакет scikit-learn для Python. рекомендую ознакомиться. Есть и более продвинутые пакеты, скажем, TensorFlow и др., но их использовать мы не будем, и ограничимся более простым scikit-learn.
Теперь о том, чего здесь не будет. Здесь не будет теории НС, разве эпизодически и оч кратко. Здесь не будет описания пакетов Python, работы с графикой и пр. Обо всем этом вы можете прочесть в интернете, книгах, и документации Python.
В топике мы будем обсуждать только применение НС к ТС и их построению.
Так как тема достаточно велика, в один топик не влезет, сегодня мы займемся самыми общими вопросами. Следующая часть будет недели через две, раньше не получается.
( Читать дальше )
Блог им. 3Qu |Думаю написать топик о ТС на нейросети.
- 24 июня 2020, 19:12
- |
Думаю написать топик о ТС на нейросети.
Разумеется, готовую ТС вы не получите, а только шаблон для ваших разработок. Ну, уж тестовый Граль мы непременно сделаем. Из ничего.
- bitcoin
- brent
- eurusd
- forex
- gbpusd
- gold
- imoex
- ipo
- nasdaq
- nyse
- rts
- s&p500
- si
- usdrub
- wti
- акции
- алготрейдинг
- алроса
- аналитика
- аэрофлот
- банки
- биржа
- биткоин
- брокеры
- валюта
- вдо
- волновой анализ
- волны эллиотта
- вопрос
- втб
- газ
- газпром
- гмк норникель
- дивиденды
- доллар
- доллар рубль
- евро
- золото
- инвестиции
- индекс мб
- инфляция
- китай
- кризис
- криптовалюта
- лукойл
- магнит
- ммвб
- мобильный пост
- мосбиржа
- московская биржа
- мтс
- нефть
- новатэк
- новости
- обзор рынка
- облигации
- опрос
- опционы
- отчеты мсфо
- офз
- оффтоп
- прогноз
- прогноз по акциям
- путин
- раскрытие информации
- ри
- роснефть
- россия
- ртс
- рубль
- рынки
- рынок
- санкции
- сбер
- сбербанк
- северсталь
- си
- сигналы
- смартлаб
- сущфакты
- сша
- технический анализ
- торговля
- торговые роботы
- торговые сигналы
- трамп
- трейдинг
- украина
- фондовый рынок
- форекс
- фрс
- фьючерс
- фьючерс mix
- фьючерс ртс
- фьючерсы
- цб
- цб рф
- экономика
- юмор
- яндекс


















