SMART-LAB
Новый дизайн
Мы делаем деньги на бирже
Блог им. bstone |Поверхности волатильности... что в них кроме Корово-Анохинцев?
- 08 ноября 2019, 19:55
- |
Я уже не однократно признавался, что торговля поверхности волатильности — это сильно заумно для меня. И более того, все время от меня ускользает ответ на такой простой вопрос: «Почему?.. Почему те, кто торгует эти поверхности (торговля улыбки — суть то же самое) думает, что рынок состоит сплошь из нобелевских лауреатов и от того умнее нас с вами?»
Что такое калибровка поверхности как не признание рыночного «ума»? Рынок настолько умен, что все рыночные цены априори правильные? Иначе зачем г-н Курбаковский старается так точно описать рыночные цены? Зачем другие коллеги калибруют улыбки и поверхности к рынку? Неужели калибруя к нему, мы любые отклонения запишем себе в профит? Да ну на...
Пусть мне не хватает этого самого ума, но мне гораздо приятнее считать, что рынок лишь на половину состоит из нобелевских лауреатов, а остальная половина — это наши любимые Корово-Анохинцы. Если последние читают этот пост, то хочу отдельно обратиться к ним: Мужики! Слушайте и дальше консультации мэтра Коровина. Я очень рад, что он снова нашел в себе силы, чтобы опуститься к вам с высоты своего опционного полета и поучить вас. Последняя его лекция, судя по всему, особенно хорошо зашла, т.к. в конце видео все хлопали и говорили ему спасибо. И действительно, спасибо вам, дорогие мои! :)
( Читать дальше )
Что такое калибровка поверхности как не признание рыночного «ума»? Рынок настолько умен, что все рыночные цены априори правильные? Иначе зачем г-н Курбаковский старается так точно описать рыночные цены? Зачем другие коллеги калибруют улыбки и поверхности к рынку? Неужели калибруя к нему, мы любые отклонения запишем себе в профит? Да ну на...
Пусть мне не хватает этого самого ума, но мне гораздо приятнее считать, что рынок лишь на половину состоит из нобелевских лауреатов, а остальная половина — это наши любимые Корово-Анохинцы. Если последние читают этот пост, то хочу отдельно обратиться к ним: Мужики! Слушайте и дальше консультации мэтра Коровина. Я очень рад, что он снова нашел в себе силы, чтобы опуститься к вам с высоты своего опционного полета и поучить вас. Последняя его лекция, судя по всему, особенно хорошо зашла, т.к. в конце видео все хлопали и говорили ему спасибо. И действительно, спасибо вам, дорогие мои! :)
( Читать дальше )
- комментировать
- ★18
- Комментарии ( 64 )
Блог им. bstone |Хитрая волатильность фьючерса
- 09 января 2019, 18:30
- |
Что-то притих наш опционный курятник. Давайте немного поразжигаем!
Уверен, что почти все уважающие себя опционщики здесь знают наше любимое уравнение Блэка-Шоулза:
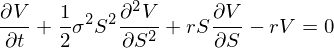
где V — стоимость опциона, S — цена акции, сигма — волатильность акции, r — безрисковая ставка
Также думаю, многие из них знают уравнение Блэка для стоимости опциона на фьючерс. Ведь по идее это оно должно быть нашим любимым на ММВБ, где мы торгуем именно такие опционы:
( Читать дальше )
Уверен, что почти все уважающие себя опционщики здесь знают наше любимое уравнение Блэка-Шоулза:
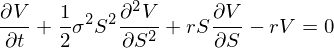
где V — стоимость опциона, S — цена акции, сигма — волатильность акции, r — безрисковая ставка
Также думаю, многие из них знают уравнение Блэка для стоимости опциона на фьючерс. Ведь по идее это оно должно быть нашим любимым на ММВБ, где мы торгуем именно такие опционы:
( Читать дальше )
Блог им. bstone |Функция нормального распределения в формулах стоимости опционов
- 25 февраля 2018, 15:21
- |
Попробую доступно показать, откуда берется в формулах стоимости опционов функция распределения Гаусса.
Итак исходное уравнение Блэка-Шоулза:
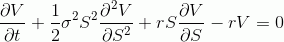
где V — цена опциона, S — цена спота, r — ставка, ну и сигма в представлении не нуждается.
Это параболическое дифференциальное уравнение в частных производных. Решать можно несколькими способами, но я не буду этого делать, а сразу запишу решение, т.к. его вывод не имеет значения для цели этого топика.
Чтобы слегка упростить запись, введу переменную времени, оставшегося до экспирации:
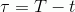
( Читать дальше )
Итак исходное уравнение Блэка-Шоулза:
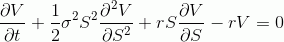
где V — цена опциона, S — цена спота, r — ставка, ну и сигма в представлении не нуждается.
Это параболическое дифференциальное уравнение в частных производных. Решать можно несколькими способами, но я не буду этого делать, а сразу запишу решение, т.к. его вывод не имеет значения для цели этого топика.
Чтобы слегка упростить запись, введу переменную времени, оставшегося до экспирации:
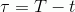
( Читать дальше )
- bitcoin
- brent
- eurusd
- forex
- gbpusd
- gold
- imoex
- nasdaq
- nyse
- rts
- s&p500
- si
- usdrub
- wti
- акции
- алготрейдинг
- анализ
- аналитика
- аэрофлот
- банки
- биржа
- биткоин
- брокеры
- валюта
- вдо
- волновой анализ
- волны эллиотта
- вопрос
- втб
- газ
- газпром
- гмк норникель
- дивиденды
- доллар
- доллар рубль
- евро
- ецб
- золото
- инвестиции
- инфляция
- китай
- коронавирус
- кризис
- криптовалюта
- лидеры роста и падения ммвб
- лукойл
- магнит
- ммвб
- мобильный пост
- мосбиржа
- московская биржа
- нефть
- новатэк
- новости
- обзор рынка
- облигации
- опек+
- опрос
- опционы
- офз
- оффтоп
- прогноз
- прогноз по акциям
- путин
- раскрытие информации
- ри
- роснефть
- россия
- ртс
- рубль
- рынки
- рынок
- санкции
- сбер
- сбербанк
- си
- сигналы
- смартлаб
- сущфакты
- сша
- технический анализ
- торговля
- торговые роботы
- торговые сигналы
- трейдер
- трейдинг
- украина
- финансы
- фондовый рынок
- форекс
- фрс
- фьючерс
- фьючерс mix
- фьючерс ртс
- фьючерсы
- цб
- шорт
- экономика
- юмор
- яндекс


















