SMART-LAB
Новый дизайн
Мы делаем деньги на бирже
Блог им. bstone
Функция нормального распределения в формулах стоимости опционов
- 25 февраля 2018, 15:21
- |
Попробую доступно показать, откуда берется в формулах стоимости опционов функция распределения Гаусса.
Итак исходное уравнение Блэка-Шоулза:
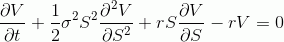
где V — цена опциона, S — цена спота, r — ставка, ну и сигма в представлении не нуждается.
Это параболическое дифференциальное уравнение в частных производных. Решать можно несколькими способами, но я не буду этого делать, а сразу запишу решение, т.к. его вывод не имеет значения для цели этого топика.
Чтобы слегка упростить запись, введу переменную времени, оставшегося до экспирации:
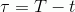
Решение уравнения БШ тогда можно записать в следующем виде:
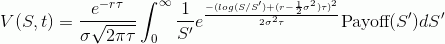
где Payoff(S) — это функция выплат опциона. Для опциона кол:
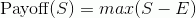
Соответственно цена кола:

поменяем переменную интегрирования на
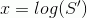
тогда
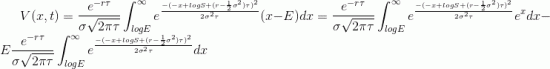
Считать стоимость опциона по этой формуле не очень просто, но рассмотрим сначала второе слагаемое:
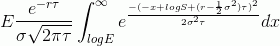
Сложно не заметить сходство с функцией нормального распределения:
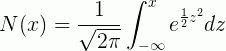
В силу популярности нормального распределения для этой функции существует немало аппроксимаций и способов вычислить ее численно. Та или иная реализация имеется, без преувеличения, в любом статистическом пакете.
Если нам удастся выразить второе слагаемое через эту функцию, то считать стоимость опционов будет намного легче. Так что овчинка стоит выделки!
Заменим переменную интегрирования во втором слагаемом выше на
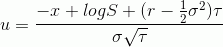
и получим
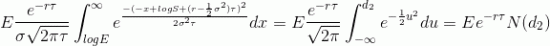
где

С первым слагаемым не так очевидно, но все же не очень сложно. Сначала надо подвести дополнительное слагаемое в экспоненте под квадрат, а далее действуем аналогично второму слагаемому. Поэтому здесь я сразу запишу результат:
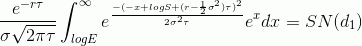
где
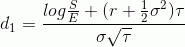
В итоге получаем, что хотели:

Ну теперь уж должно быть очевидно, что функция распределения Гаусса в формулах стоимости опционов БШ не более чем очень удачный способ упростить вычисление интегралов в исходном решении уравнения БШ.
Это очень элегантная техническая деталь но тот факт, что дельта опциона выражается через N(x) — всего лишь следствие записи производной от V(S,t) по S с использованием преобразований, аналогичным использованным выше, и никакого отношения к вероятности выхода опциона в деньги он не имеет.
Итак исходное уравнение Блэка-Шоулза:
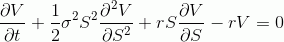
где V — цена опциона, S — цена спота, r — ставка, ну и сигма в представлении не нуждается.
Это параболическое дифференциальное уравнение в частных производных. Решать можно несколькими способами, но я не буду этого делать, а сразу запишу решение, т.к. его вывод не имеет значения для цели этого топика.
Чтобы слегка упростить запись, введу переменную времени, оставшегося до экспирации:
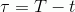
Решение уравнения БШ тогда можно записать в следующем виде:
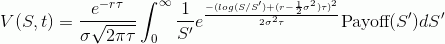
где Payoff(S) — это функция выплат опциона. Для опциона кол:
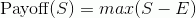
Соответственно цена кола:

поменяем переменную интегрирования на
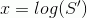
тогда
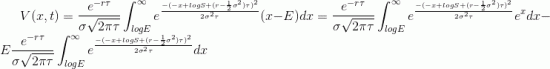
Считать стоимость опциона по этой формуле не очень просто, но рассмотрим сначала второе слагаемое:
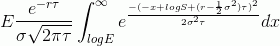
Сложно не заметить сходство с функцией нормального распределения:
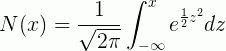
В силу популярности нормального распределения для этой функции существует немало аппроксимаций и способов вычислить ее численно. Та или иная реализация имеется, без преувеличения, в любом статистическом пакете.
Если нам удастся выразить второе слагаемое через эту функцию, то считать стоимость опционов будет намного легче. Так что овчинка стоит выделки!
Заменим переменную интегрирования во втором слагаемом выше на
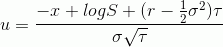
и получим
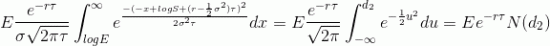
где

С первым слагаемым не так очевидно, но все же не очень сложно. Сначала надо подвести дополнительное слагаемое в экспоненте под квадрат, а далее действуем аналогично второму слагаемому. Поэтому здесь я сразу запишу результат:
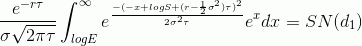
где
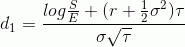
В итоге получаем, что хотели:

Ну теперь уж должно быть очевидно, что функция распределения Гаусса в формулах стоимости опционов БШ не более чем очень удачный способ упростить вычисление интегралов в исходном решении уравнения БШ.
Это очень элегантная техническая деталь но тот факт, что дельта опциона выражается через N(x) — всего лишь следствие записи производной от V(S,t) по S с использованием преобразований, аналогичным использованным выше, и никакого отношения к вероятности выхода опциона в деньги он не имеет.
1.5К |
Читайте на SMART-LAB:

Итоги первичных размещений ВДО и некоторых розничных выпусков на 2 марта 2026 г.
Следите за нашими новостями в удобном формате: Telegram , Youtube , RuTube, Smart-lab , ВКонтакте , Сайт
18:34

NAT.GAS: Газовый арбитраж на пороге взрыва — зажжет ли Европа американский хаб?
На европейских рынках котировки на природный газ (TTF) сегодня взлетели на 45%, превысив отметку €46/МВт·ч ($570 за 1000 м³). Европа критически...
22:26
теги блога bstone
- Intraday
- LUA
- Ri
- SR
- Аллирог
- аналитик
- аналитика
- биржа
- Блэк-Шоулз
- бонус
- брокеры
- вероятность
- визуализация сделок
- Волантильность
- волатильность
- волны эллиота
- Волотильность
- герчик
- демо форекс
- депо
- депозит
- Дискреционный трейдинг
- ДУ
- интрадей
- книга
- Книги
- Коровин
- короткий стоп
- кризис
- кукл
- лчи
- лчи 2015
- Маркидон
- мобильный пост
- Нефть
- опрос
- опцион
- опционы
- опыт
- открытие брокер
- оффтоп
- просадка
- психология трейдинга
- развод
- рецензии
- рецензия
- риск
- роботы
- рублебакс
- рынок
- Сбер
- сбербанк
- Сбой на бирже
- сделки
- семинар Герчика
- си
- скальп
- слив
- смартлаб
- стакан
- стоп
- Стоп-лосс
- ТА
- технический анализ
- торговые роботы
- трейдер
- трейдинг
- улыбка волатильности
- уровни
- шорты
- Эллиот
- юмор





















я мехматов не кончал, хотя и прослушал два курса по высшей математике, слишком давно было, ничего уже не помню.
Дельта может и не равна вероятности выхода опциона в деньги. Но очень сильно с ней коррелирует, так?
И вообще, если вокруг опционов построена такая обширная математическая модель, неужели нет ни одного грека, который бы показывал вероятность выхода опциона в деньги? Не дельта ли ближе всего к этой вероятности?
(1) — логнормальное случайное блуждание (dX — Винеровский процесс)
(2) — портфель, состоящий из опциона и обратной позиции по БА
(3) — изменение портфеля на каждом шаге
(4) — изменение стоимости опциона (следует из (1) и леммы Ито)
(5) — хеджирующая позиция по БА убирает случайную составляющую из портфеля
(6) — принцип не арбитража
Если подставить (2) и (5) в (6), получим уравнение БШ. Т.е. уравнение динамики стоимости опциона при условии, что арбитражной халявы нет, случайные риски полностью захеджированы, а цена блуждает логнормально.
По поводу IV и улыбки. На мой взгляд это вообще вопрос веры по большей части. Очень субъективная вещь. Лично я не фанат анализа улыбки и торговли на этой основе, т.к. не вижу тут никакой смысловой базы. По большей части я считаю улыбку результатом жадности, спекуляций, и не достаточно глубокого понимания механики ценообразования опционов большой массой участников.
На сколько видел в оригинальной работе, там авторы шутканули как они типа легко и очевидно решили своё дифф. уравнение, ничего не объясняя...
А подход от теорвера как-то последовательнее понятнее выглядит, что вот стоимость=мат. ожидание, с такой-то плотностью поинтегрировали, выводим и приходим к нормальным распределениям...
=) Мне что-то не нравятся Ваши формулы в интегральной форме.
Они сразу в явном виде содержат указание на Гауссов процесс.
То есть в такой форме неочевидно как заменить броуновское движение на более реалистичный случайный процесс?..
Жаль, уже нельзя пост плюсануть...
bstone, разве оно реально нужно для вывода этого дифура?..
Хм!.. К стыду своему подзабыл подробности...
Тогда вообще беда получается в этом смысле?