Это исследование я сделал под влиянием бурной дискуссии на форуме  о распределении «хвостов» приращений логарифмов цен, возникшей, казалось, на «пустом месте»: насколько корректны доверительные интервалы для оценок параметров линейной регрессии в альфа-бета модели?

Кроме указанной ссылки, дискуссия продолжилась в еще двух ветках: тут и тут.

Действительно, эти оценки в классическом случае строятся на основе центральной предельной теоремы для статистик оценок параметров линейной регрессии. Однако, как я уже писал на смартлабе, необходимым условием которой является скорость роста дисперсии суммы слагаемых как О(N), N – число слагаемых, а для быстрой сходимости в центральной области еще и требуется конечность абсолютного третьего момента любого слагаемого (если говорить о сходимости на всей прямой, включая «большие уклонения»,  то еще требуется  и конечность всех моментов отдельных слагаемых). Однако эти условия не выполняются для части распределений Парето и Стьюдента с полиномиальной скоростью убывания «хвостов» и поэтому для «хорошего» приближения суммы таких слагаемых нормальным законом требуется очень большое число испытаний, которых, как правило, в альфа-бета модели, построенной на дневных данных, нет. А значит традиционные методы построения доверительных интервалов для оценок параметров этой модели «не работают».

( Читать дальше )

В теме опционов часто поднимается вопрос о причинах появления «ухмылки волатильности» в опционах на фондовые индексы. Или, проще говоря, почему опционы пут  «вне денег», на страйке лежащем на n% от текущей цены дороже опционов колл «вне денег», лежащих на том же «расстоянии» от текущей цены.

Даже цитируются «умные» книги о том, что спрос на путы больше из-за наличия хэджеров.

На самом деле все проще и иначе.

Вот общее определение «справедливой» цены произвольного платежного поручения

Итак, пара общих определений.
Платежное поручение — это обязательство продавца выплатить некоторую сумму покупателю, зависящую от цены базового актива в будущий момент времени Т — С(Т).
Платежной функцией платежного поручения называется функция выплат f(C(T)).

Тогда справедливой ценой платежного поручения можно считать среднее f(C(T)) по распределению будущей цены С(Т) (чаще всего неизвестному точно), деленную на 1+R, где R- безрисковая ставка до момента времени Т.

( Читать дальше )

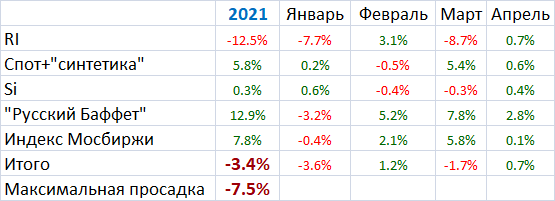
Начнем с традиционной таблицы 

 

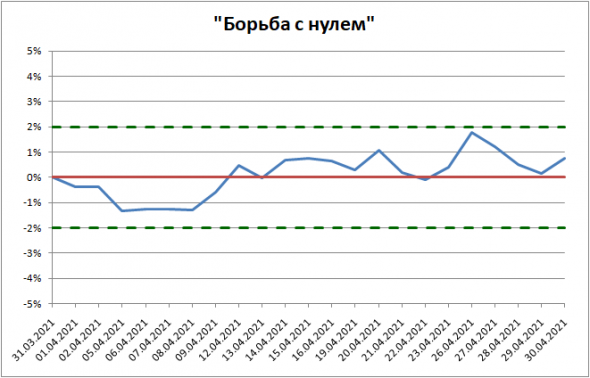
Писать об отдельных системах в такой месяц и нечего, потому что все в заголовке. Приведу только график динамики счета, который наглядно подтверждает заголовок

 

( Читать дальше )

Третий день максимум дня 5945.

Я ни раз и ни два говорил, что политика «таргетирования инфляции» — это диверсия против экономики России. Вот просто цифры



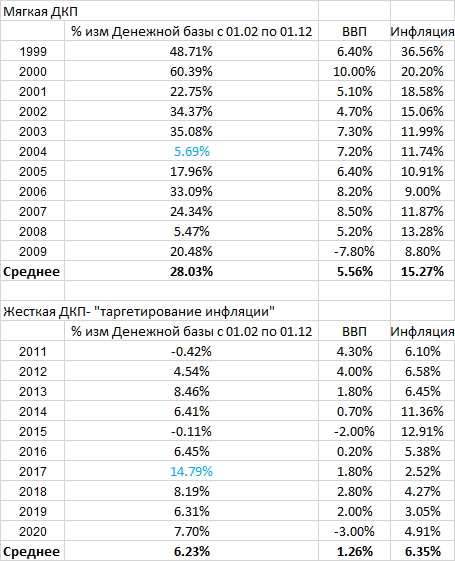
Если взглянуть на строку средних, то кому еще не очевидно сказанное мною в начале топика?

Но, глядя в таблицы, возникает два естественных вопроса:
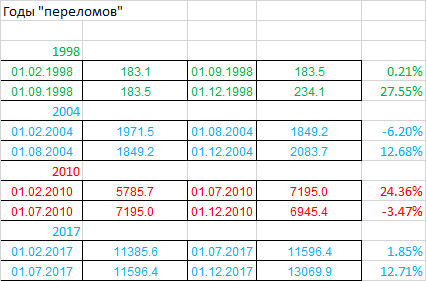
— почему нет 1998-го и 2010?
— что было в 2004-м и 2017-м, явно выбивающимися из общей тенденции? (с 2008-м все понятно — кризис)

Ответы на них мы находим в разбиении этих годов на два периода



( Читать дальше )

В КГБ после аварии совершенно официально, но под запретом распространения  сотрудникам доводилась информация расследования, в которой говорилось, что  это был не «плановый эксперимент», а ускоренная остановка реактора, применявшаяся персоналом неоднократно с целью сокращения рабочего времени. Такая остановка противоречила правилам эксплуатации, но «до поры до времени сходила с рук».

И еще одно событие 1986-го, уже коснувшееся меня. Будучи куратором лаборатории при Украинской Академии наук, я должен был дважды в год в мае и октябре ездить в Киев и принимать отчеты о проделанной работе. Так вот, в мае 1986-го руководство управления приняло решение, что отчет пройдет не в Киеве, а в Москве. В октябре 1986-го я уже по традиции поехал в командировку в Киев.

Прежде всего определим, что такое «околорынок». В данном топике под околорынком будем понимать любую возмездную (!) деятельность, связанную с финансовым рынком, кроме торговли на собственных средствах и оказании  услуг по ее реализации (организованные торги, брокерские услуги, депозитарный учет  и т. д.).

Так ли плох околорынок? Отнюдь. Почему?

Первое и главное, что должен понять любой, приносящий деньги на финансовый рынок: любая торговля на этом рынке, кроме покупки индексных фондов — это профессия. И, соответственно, для достижения успеха надо эту профессию, как минимум, освоить. А это требует времени и желания. Это раз.

Два. Что плохого в том, что человек, решивший стать профессионалом, стремится к увеличению масштабов решаемых задач, используя для этого все возможные и законные способы? Ничего. Более того, верно обратное: нет такого стремления — нет профессионального роста. Так было, есть и будет в любой профессии.

Что из себя представляет масштаб на финансовом рынке? Как бы не осуждалась меркантильность, но в нашей  области масштаб — это количество денег на своем счете, которыми профессионал торгует. Причем совершенно необязательно источником увеличения этих средств должен  быть только % доходности торговли. А откуда взять другие источники профессионалу только в области торговли? Как ни крути, но только с околорынка в том определении, которое мы дали выше.

( Читать дальше )

Вот такую зaставку мне сегодня показывает Windows

winestyle.ru/articles/wine/portwein-777-story.html