Недавно потребовалось установить экспоненту Парето хвоста распределения вероятностей. И чтобы посмотреть насколько хорошо методы EVT работают, я сделал простой пример.
Пример: 30 сэмплов StudentT(df=4), каждый размером 20000. Определить экспоненту хвоста используя методы: Хилла, GPD, LeastSquares, CDF LogLog PLot.
Результаты ужасны: точность всех методов плюс минус километр. Я не вижу ни малейшего смысла в EVT поскольку вручную по линейке установить наклон линии на ЛогЛог Графике CDF оказывается не хуже (мне кажется даже лучше) чем специализированные методы EVT.
На графике — y — найденная экспонента хвоста, каждая линия это отдельный сэмпл, цвет метод определения, х — гиперпараметр (число точек в хвосте распределения которые использовались в расчетах). Верный результат это горизонтальная линия y=4, вместо этого мы наблюдаем, в зависимости от метода — систематические ошибки, либо дикий хаос.


Даже, мне кажется с линейкой предпочтительней, график лог лог. Поскольку ты боль менее визуально и интуитивно понимаешь что делаешь. 

( Читать дальше )

Много методов: Hill, EVT GPT, регрессия. И все с точностью километр. На графике — 30 симуляций: 30 сэмплов StudentT(df=4) 20к, для каждого сэмпла определяется df различным эстиматором (цвет линии), ось х — значение трешхолда эстиматора. 


Правильный результат — постоянная линия с y=4. Единственный нормальный результат (красные линии) это MLE полного распределения, но это именно что эстиматор полного распределение, а не Tail Estimator. Среди хвостовых эстиматоров ни одного хорошего.

EVT GPT на который я больше всего расчитывал (синии линии), вообще ничего не измеряет (но возможно я допустил ошибку и неверно его считаю, по идее он должен быть самый точный).

Подробней www.reddit.com/r/nassimtaleb/comments/1mdwqjw/huge_errors_in_heavy_tail_estimators_hill_evt_gpt/
Код gist.github.com/al6x/11e66ab92c525f2ef2c1510e6ac7a3f7

Получается неверный результат если есть ассиметричность, настоящее значение 4, но он неверно определяет как 3 для левого и 5 дле правого хвоста. Или, скорей дело не в Hill а само распределение искажает хвосты? Никто не сталкивался? код



На графике две линии должны стабилизироваться на отметке 4, а они показывают 3 и 5.

Юля на мой взгляд лучше для понимания чем Питон, так сказать Matlab для рабочего человека :) (даже, Юля лучше чем Матлаб)


Питон



( Читать дальше )

Я почти не использую 3D графики, на них сложно что то рассмотреть.
Случайно увидел вариант графика ниже, выглядит вполне понятно, попробую подобные построить.
Кто еще знает интересные 3D варианты, распределения и не только, скиньте в коментах скриншоты плиз.

Старые но очень хорошие материалы по визуализации данных. Это радикально другой подход, декларативный, по сравнению с Matlab, MatplotLib и т.п. императивным подходом. Он позволяет структурно думать о визуальном представлении данных, что то вроде SQL для графиков.





VegaLite observablehq.com/@uwdata/introduction-to-vega-lite
И Altair от его создателя www.youtube.com/watch?v=ms29ZPUKxbU

Вега и Альтаир это одно и тоже, вега многословна но хороша для обучения и понимания как это работает, альтаир то что используется на практике, гораздо короче и компактней.

Эти вещи позволяют по другому взглянуть на то что такое графики, увидеть их структуру. Даже если продолжить пользоваться Матлабом и Матплотлибом, представление о том что на графике уже будет выглядеть по другому.

Видео www.youtube.com/watch?v=iqq6hCbU0mo документ и исходники github.com/al6x/profit_hunting/tree/main/option_norm



( Читать дальше )

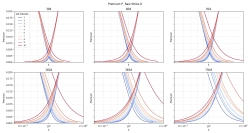
При нормализации страйков К как вероятность p = P(S_T < K), получается линейная зависимость OTM премиума от страйка (ОТМ до/после p=0.5), ИТМ часть нелинейна.


P(S_T < K) = F(d2) из Black Scholes

Против самого d2 OTM тоже линейна, но по другому



( Читать дальше )

Есть 4 варианта нормализовать страйки опционов, цель — чтобы К были одинаковы для разных (цен акций, периодов экспирации, волатильностей):

Что лучше — совершенно точный но неверный результат, или приближенный, но в целом верный?

— [точный] F(d2) через IV, получаем точные значения, соответствующие ожиданиям рынка. Интерполяция, очень точно.
— [приближенный и искаженный] Предсказать mu, sigma на момент экспирации, на основе исторических данных, и получить F(d2) через них. Экстраполяция, не точно, и ошибка в концепции, не учитывается форма (ассиметричность, хвосты) распределения.
— [приближенный и ненадежный] Предсказать полное распределения на момент экспирации аналитически SkewStudentT(mu, sigma, skew, freedom), расчитать F(d2) через него. Концепция верная, но это экстраполяция и результат не точный, причем может быть сильно не точным из за ошибок в mu.
— [приближенный и мало полезный] Предсказать полное распределения на момент экспирации эмпирически как численная CDF, расчитать F(d2) через него. Концепция верная, но это экстраполяция и результат не точный, но он не зависит от среднего и других параметров и несколько более надежен чем аналитич формула. Но, с численной CDF сложно работать, нельзя сделать точную подгонку и т.п.

( Читать дальше )

Нормализация страйков, чтобы для каждого периода и волатильности были одинаковые значения страйков. 


На графике:

• x нормализованные страйки K,
• y вероятность попадания опциона в ITM, в лог маштабе, CDF(K) p<0.5 и SurvivalFn(K) p>0.5 
• цвет — волатильность (дециль),
• каждая группа — это отдельный период [30, 60, 91, 182, 365, 730]. Периоды искуственно сдвинуты вверх чтобы отличить, в реальности все периоды также сливаются в одну линию.

По сути это график d2 vs F(d2).

Нормализация:

mean = log(E[S_T/S_0]) — 0.5sigma^2
d2 = (log K/S_0 — mean)/sigma

Этот же график, только каждый период на отдельном графике и в линейном маштабе.


( Читать дальше )