SMART-LAB
Новый дизайн
Мы делаем деньги на бирже
bstone
Продолжаем
- 30 марта 2018, 12:11
- |
Исправил отображение предыдущих улыбок. В старом ролике корректно отображалась только текущая, а предыдущие сдвигались:
( Читать дальше )
( Читать дальше )
- комментировать
- 3.4К | ★2
- Комментарии ( 3 )
Вид сбоку - "денежность"
- 26 марта 2018, 23:20
- |
Новые данные выгрузить не успел сегодня, поэтому решил глянуть на вчерашние с точки зрения «денежности» ( -log(F/K) ):
Анимационная улыбка
- 25 марта 2018, 22:11
- |
Прогнал биржевую улыбку на RTS-6.18 с начала года. За неимением лучших данных на выходных брал расчетные цены клирингов. Такая вот развлекуха.
Гораздо проще, чем платные закрытые блоги
- 16 марта 2018, 01:37
- |
Думаю весь смарт будет аплодировать стоя если: все посты по крипте, а также посты, начинающиеся с видео, а также посты с «Krechetov» в начале названия будут автоматом заруливаться в закрытый блог :)
Вишенкой на торте будет кнопка «В закрытый блог», которая будет навсегда убирать посты автора из потока для пользователя, ее нажавшего. Сейчас для достижения такого эффекта приходится заносить людей в ЧС, а они потом обнаруживают, что не могут задать воарос или оставить комментарий, чувствуют себя г***ом ну и т.д. :)
Ну и авансом за реализацию этих фич рассказываю как срубить бабла на контенте без всяких платных блогов: ужимаем загружаемые картинки до качества 5% (а не 10% как сейчас — некоторым все-таки удается прочитать там заглавные буквы) и добавляем кнопку «Купить» к каждой картинке. При оплате открывать картинку в более высоком качестве. Важно не показывать сразу в оригинальном качестве после первой оплаты, а делать это постепенно: заплатил 100 рублей — увидел на 5% меньше сжатия. Это нужно для того, чтобы заплатив 1000 рублей пользователь мог разглядеть изображение в 50% качестве и понять, что там нет ничего важного для него, и не оплачивать полностью оригинальный размер — мы же не звери какие-то :))
Голосуйте за развитие смартлаба плюсами!
Вишенкой на торте будет кнопка «В закрытый блог», которая будет навсегда убирать посты автора из потока для пользователя, ее нажавшего. Сейчас для достижения такого эффекта приходится заносить людей в ЧС, а они потом обнаруживают, что не могут задать воарос или оставить комментарий, чувствуют себя г***ом ну и т.д. :)
Ну и авансом за реализацию этих фич рассказываю как срубить бабла на контенте без всяких платных блогов: ужимаем загружаемые картинки до качества 5% (а не 10% как сейчас — некоторым все-таки удается прочитать там заглавные буквы) и добавляем кнопку «Купить» к каждой картинке. При оплате открывать картинку в более высоком качестве. Важно не показывать сразу в оригинальном качестве после первой оплаты, а делать это постепенно: заплатил 100 рублей — увидел на 5% меньше сжатия. Это нужно для того, чтобы заплатив 1000 рублей пользователь мог разглядеть изображение в 50% качестве и понять, что там нет ничего важного для него, и не оплачивать полностью оригинальный размер — мы же не звери какие-то :))
Голосуйте за развитие смартлаба плюсами!
Англичанка гадит... красиво?
- 14 марта 2018, 20:08
- |
Ничто не предвещало беды и позавчера я решил пропылесосить заявки миллионеров Анохиных в дальних квартальных коллах. Позу набрал практически за одну сессию с вечера и до клиринга. В двух страйках анохинцы брали особенно жадно, в остальных — так себе.
Но в целом рыбалка удалась и скромный фундамент в 37% годовых с вероятностью 80% на экспирацию был таки заложен.
В общем хороший повод расслабиться, но тут входит она и всё гадит. Поза в ужасе плюсует на 46% годовых за день, а я на измене, т.к. больше половины профита по веге и с этим надо что-то делать.
В общем прикинув немного, решил залочить профит ценой дополнительного ГО. Занейтралил греки. Фактически по букварю фигур я сейчас в зигзаге.
Если штанишки не лопнут и я донесу комплект до экспирации, то вполне могу рассчитывать на ~90% годовых за квартал. Проблема только в том, что управлять такой позицией будет сложнее. Это тебе не «купил и держи… дельту в нуле». Плюс еще при худшем раскладе ближе к экспирации это будет реальная борьба с риск менеджментом брокера. Но душа лудомана-оптимиста как бы намекает, что бывает еще и лучший расклад :)
Такая вот она, англичанка!
Но в целом рыбалка удалась и скромный фундамент в 37% годовых с вероятностью 80% на экспирацию был таки заложен.
В общем хороший повод расслабиться, но тут входит она и всё гадит. Поза в ужасе плюсует на 46% годовых за день, а я на измене, т.к. больше половины профита по веге и с этим надо что-то делать.
В общем прикинув немного, решил залочить профит ценой дополнительного ГО. Занейтралил греки. Фактически по букварю фигур я сейчас в зигзаге.
Если штанишки не лопнут и я донесу комплект до экспирации, то вполне могу рассчитывать на ~90% годовых за квартал. Проблема только в том, что управлять такой позицией будет сложнее. Это тебе не «купил и держи… дельту в нуле». Плюс еще при худшем раскладе ближе к экспирации это будет реальная борьба с риск менеджментом брокера. Но душа лудомана-оптимиста как бы намекает, что бывает еще и лучший расклад :)
Такая вот она, англичанка!
Формула для расчета вероятности выхода опциона в деньги
- 25 февраля 2018, 18:50
- |
Чтобы окончательно поставить точку в вопросе о том, почему дельта опциона не равна вероятности выхода опциона в деньги, давайте просто посчитаем эту вероятность.
Для экономии места и времени я буду использовать кое-какие обозначения и преобразования, которыми я пользовался в посте "Функция нормального распределения в формулах стоимости опционов".
Рассмотрим логнормальное случайное блуждание:
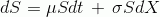
где dX — Винеровский процесс.
Определим вероятность того, что цена из начальной точки S во время t окажется в диапазоне от a до b во время t':
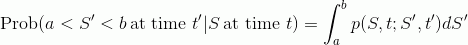
( Читать дальше )
Для экономии места и времени я буду использовать кое-какие обозначения и преобразования, которыми я пользовался в посте "Функция нормального распределения в формулах стоимости опционов".
Рассмотрим логнормальное случайное блуждание:
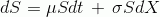
где dX — Винеровский процесс.
Определим вероятность того, что цена из начальной точки S во время t окажется в диапазоне от a до b во время t':
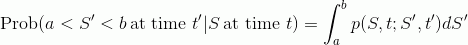
( Читать дальше )
Функция нормального распределения в формулах стоимости опционов
- 25 февраля 2018, 15:21
- |
Попробую доступно показать, откуда берется в формулах стоимости опционов функция распределения Гаусса.
Итак исходное уравнение Блэка-Шоулза:
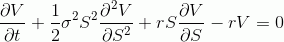
где V — цена опциона, S — цена спота, r — ставка, ну и сигма в представлении не нуждается.
Это параболическое дифференциальное уравнение в частных производных. Решать можно несколькими способами, но я не буду этого делать, а сразу запишу решение, т.к. его вывод не имеет значения для цели этого топика.
Чтобы слегка упростить запись, введу переменную времени, оставшегося до экспирации:
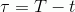
( Читать дальше )
Итак исходное уравнение Блэка-Шоулза:
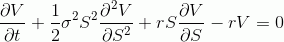
где V — цена опциона, S — цена спота, r — ставка, ну и сигма в представлении не нуждается.
Это параболическое дифференциальное уравнение в частных производных. Решать можно несколькими способами, но я не буду этого делать, а сразу запишу решение, т.к. его вывод не имеет значения для цели этого топика.
Чтобы слегка упростить запись, введу переменную времени, оставшегося до экспирации:
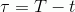
( Читать дальше )
Ноль на счету...
- 25 января 2018, 09:41
- |
Нет… ни один из моих счетов не пострадал. Это просто старый творческий порыв, который наконец удалось привести в удобоваримый вид. Да еще и к такой дате! Петь обязательно :)
Если вы не дружите с математикой, не давайте в ДУ
- 23 января 2018, 10:06
- |
Мужики, ну сто раз уже разжевывали. Прям не ожидал от Тимофея. Сначала этот бред про шум-тренд и торговлю тонкого рынка крипты с 100-м плечом, теперь еще эти 20% против 25%. Ладно, если б это была запредельная высшая математика...
Допустим депозит 100к:
1) Фиксированная ставка (арифметическая прогрессия), теряем в одной сделке 10к. После 5-ти лосей подряд:
100к-5*10к=50к
Потеряли 50%, а отбить надо целых 100%, о мой бог! Для этого нам потребуется целых 5 (пять, Карл!) прибыльных сделок по 10к:
50к+5*10к = 100к
Намного это сложнее, чем 5 лосей по 10к? На целых ноль сделок.
2) Пропорциональная ставка (геометрическая прогрессия), теряем 10% в одной сделке. После пяти убыточных:
100к*0.9^5 = 59049
Потеряли 41%, а отбить надо целых 69.3%, о мой бог! Для этого нам понадобится целых 5 сделок с прибылью 11.11%:
59049*1.1111^5=99995
или 6 сделок с прибылью 10%:
59049*1.1^6=104608
или всего на одну сделку больше (я бы даже сказал на половину сделки). Невыполнимо?
Так что это не та причина, по которой не стоит давать в ДУ.
Но имейте в виду, что цифры в примерах выше завышены для наглядности и не являются руководством к действию :)
Допустим депозит 100к:
1) Фиксированная ставка (арифметическая прогрессия), теряем в одной сделке 10к. После 5-ти лосей подряд:
100к-5*10к=50к
Потеряли 50%, а отбить надо целых 100%, о мой бог! Для этого нам потребуется целых 5 (пять, Карл!) прибыльных сделок по 10к:
50к+5*10к = 100к
Намного это сложнее, чем 5 лосей по 10к? На целых ноль сделок.
2) Пропорциональная ставка (геометрическая прогрессия), теряем 10% в одной сделке. После пяти убыточных:
100к*0.9^5 = 59049
Потеряли 41%, а отбить надо целых 69.3%, о мой бог! Для этого нам понадобится целых 5 сделок с прибылью 11.11%:
59049*1.1111^5=99995
или 6 сделок с прибылью 10%:
59049*1.1^6=104608
или всего на одну сделку больше (я бы даже сказал на половину сделки). Невыполнимо?
Так что это не та причина, по которой не стоит давать в ДУ.
Но имейте в виду, что цифры в примерах выше завышены для наглядности и не являются руководством к действию :)
теги блога bstone
- Intraday
- LUA
- Ri
- SR
- Аллирог
- аналитик
- аналитика
- биржа
- Блэк-Шоулз
- бонус
- брокеры
- вероятность
- визуализация сделок
- Волантильность
- волатильность
- волны эллиота
- Волотильность
- герчик
- демо форекс
- депо
- депозит
- Дискреционный трейдинг
- ДУ
- интрадей
- книга
- Книги
- Коровин
- короткий стоп
- кризис
- кукл
- лчи
- лчи 2015
- Маркидон
- мобильный пост
- Нефть
- опрос
- опцион
- опционы
- опыт
- открытие брокер
- оффтоп
- просадка
- психология трейдинга
- развод
- рецензии
- рецензия
- риск
- роботы
- рублебакс
- рынок
- Сбер
- сбербанк
- Сбой на бирже
- сделки
- семинар Герчика
- си
- скальп
- слив
- смартлаб
- стакан
- стоп
- Стоп-лосс
- ТА
- технический анализ
- торговые роботы
- трейдер
- трейдинг
- улыбка волатильности
- уровни
- шорты
- Эллиот
- юмор























