SMART-LAB
Новый дизайн
Мы делаем деньги на бирже
Блог им. Buybuy
Математическая задачка № 5 (окончание)
- 04 февраля 2019, 04:49
- |
Доброй ночи, коллеги!
Чтобы прервать предыдущее обсуждение, которое в самом деле зашло в никуда, открываю новый топик. Надеюсь, я вам еще не надоел.
Задачка решается очень просто. Даже в более общей формулировке.
Пусть у нас есть рулетка, на которой мы с вероятностью P выигрываем 1:1, с вероятностью (1-P) проигрываем 1:1.
В случае классической европейской рулетки (с одним зеро) P=18/37.
Денежный масштаб тоже изменим — откажемся от долларов. Надо из 0.1 сделать 1 (все поделили на $10,000).
Попробуем все же посчитать вероятность.
Ниже приведено короткое решение, поместившееся на экран моего Galaxу Note:
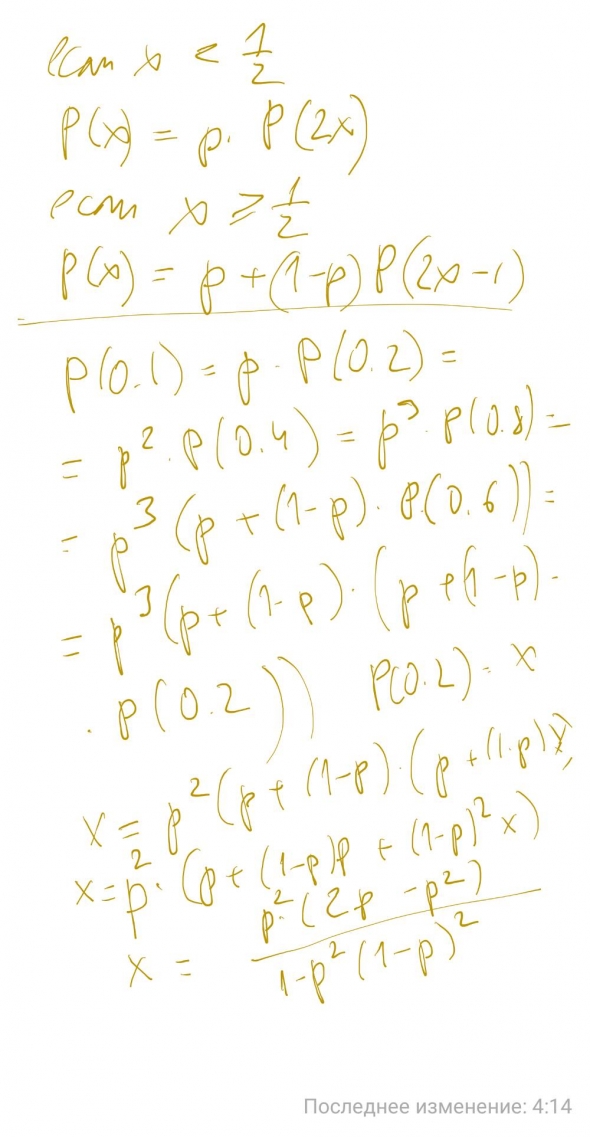
Несколько пояснений:
P(x) — вероятность достичь цели (1) с начальным капиталом x
Т.е. надо определить P(0.1)
Если x меньше половины, то его следует удвоить (с вероятностью P), а затем продолжать с отметки P(2x)
Если x больше или равен половине, то следует достичь цели с одного удара (с вероятностью P), а в случае неудачи продолжить с отметки P(2x-1)
Далее (да, понимаю, это коряво) за x уже принимается P(0.2). При этом P(0.1)=P*P(0.2)
В итоге получаем P(0.1)=P^3*(2*P-P^2)/(1-P^2*(1-P)^2)
Теперь подставляем P=18/37 и, о чудо, P(0.1)=9.04182%
Таким образом:
1. Eugene Logunov блестяще все посчитал
2. wrmngr блестяще все прикинул на глаз
Хотя можно было и на калькуляторе…
Чтобы прервать предыдущее обсуждение, которое в самом деле зашло в никуда, открываю новый топик. Надеюсь, я вам еще не надоел.
Задачка решается очень просто. Даже в более общей формулировке.
Пусть у нас есть рулетка, на которой мы с вероятностью P выигрываем 1:1, с вероятностью (1-P) проигрываем 1:1.
В случае классической европейской рулетки (с одним зеро) P=18/37.
Денежный масштаб тоже изменим — откажемся от долларов. Надо из 0.1 сделать 1 (все поделили на $10,000).
Попробуем все же посчитать вероятность.
Ниже приведено короткое решение, поместившееся на экран моего Galaxу Note:
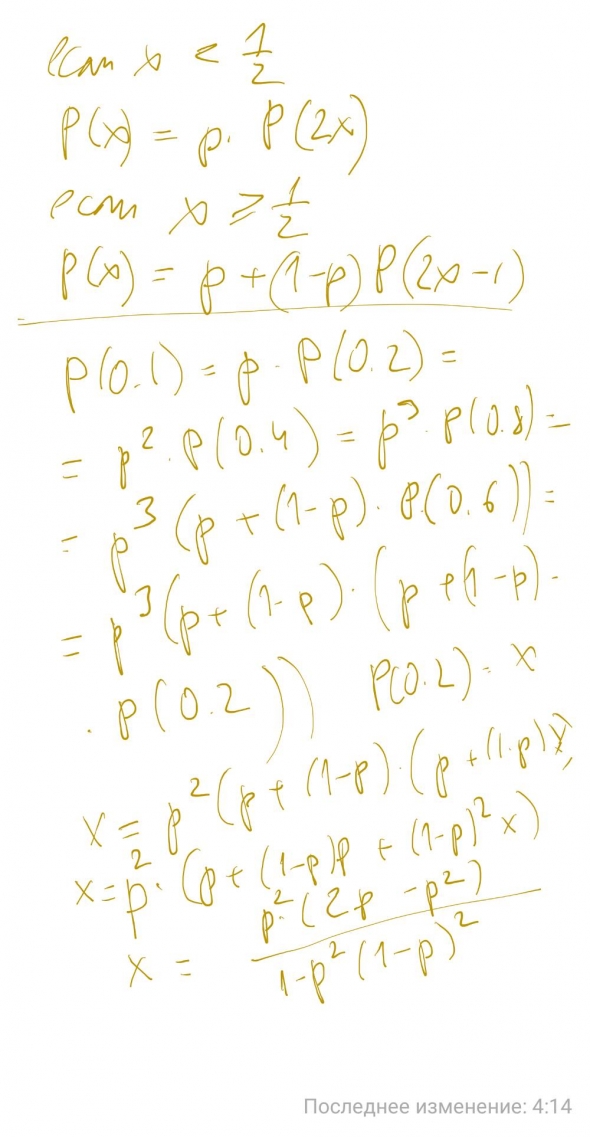
Несколько пояснений:
P(x) — вероятность достичь цели (1) с начальным капиталом x
Т.е. надо определить P(0.1)
Если x меньше половины, то его следует удвоить (с вероятностью P), а затем продолжать с отметки P(2x)
Если x больше или равен половине, то следует достичь цели с одного удара (с вероятностью P), а в случае неудачи продолжить с отметки P(2x-1)
Далее (да, понимаю, это коряво) за x уже принимается P(0.2). При этом P(0.1)=P*P(0.2)
В итоге получаем P(0.1)=P^3*(2*P-P^2)/(1-P^2*(1-P)^2)
Теперь подставляем P=18/37 и, о чудо, P(0.1)=9.04182%
Таким образом:
1. Eugene Logunov блестяще все посчитал
2. wrmngr блестяще все прикинул на глаз
Хотя можно было и на калькуляторе…
теги блога Мальчик buybuy
- экономиках
- Android
- deep learning
- eurrub
- forex
- Google Play Market
- LMAX
- S&P500
- telegram
- автомобили
- активы
- акции
- алгоритмическая торговля
- альфа-банк
- анекдот
- банки
- Вассерман
- ВВП России
- Газпром
- государство
- делимся интересными фильмами
- деприватизация
- Дерипаска
- доверительное управление
- доллар рубль
- Дональд Трамп
- жильё
- ЗОЖ
- золото
- инвестиции
- инвестиции в недвижимость
- инфляция
- инфоцыгане
- искусственный интеллект
- Казахстан
- Китай
- коронавирус
- криптовалюта
- лчи 2019
- недвижимость
- Нефть
- Новости
- Общее образование
- Общее развитие
- опрос
- опционы
- оффтоп
- Павел Дуров
- Политика
- политсрач
- Прогнозы
- русал
- рынок труда РФ
- с новым годом
- санкции
- СВО
- слово пацана
- смартлаб
- СПГ
- США
- технический анализ
- торговая система
- торговля
- торговые роботы
- Торговые терминалы
- трейдинг
- Украина
- физическое золото
- философия
- фильмы про биржу и трейдинг
- форекс
- экономика России
- юмор



















Не помогут вам эти все задачки чтобы понять рынок, вы совсем уже ушли в другую сторону. Рынок может никогда этого не простить
куб то откуда? квадрат же
Для P(0.2) — квадрат. Р(0.1)=P*P(0.2)