SMART-LAB
Новый дизайн
Мы делаем деньги на бирже
Блог им. 3Qu
Сравнение ЕМА и фильтра Баттерворта 2-го порядка.
- 24 января 2020, 20:39
- |
В связи с моим топиком Фильтр Гаусса N-ного порядка как индикатор, в комментариях возник вопрос сравнения задержек фильтра Баттерворта 2-го порядка и ЕМА.
Для сравнения групповых задержек различных фильтров обычно сравнивают их отклики на единичный скачок 1(t). Это, типа, ступенька высотой 1.
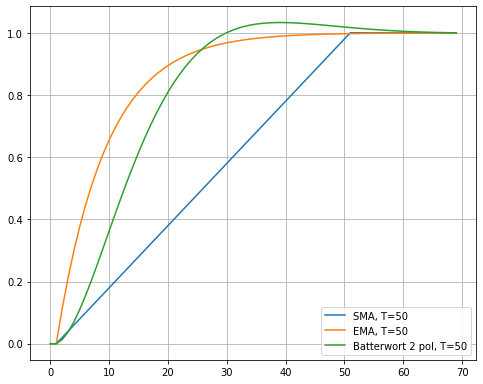
На рисунке сравниваются отклики на единичный скачок 2-х фильтров с периодом 50. SMA с периодом 50 приведена здесь как калибровочная.
Из рисунка можно видеть, что групповая задержка фильтра Баттерворта при одинаковом периоде Т составляет по уровню 0.5 на ~5 отсчетов больше чем у ЕМА.
Простите, а что-же вы хотели увидеть, если фильтром Баттерворта мы обрезали ВЧ часть спектра сигнала? ЕМА плохо подавляет ВЧ компоненты сигнала, отсюда и такая нервная реакция на любой чих.
Спрашивается, а зачем тогда вообще фильтр, если он мало что подавляет?
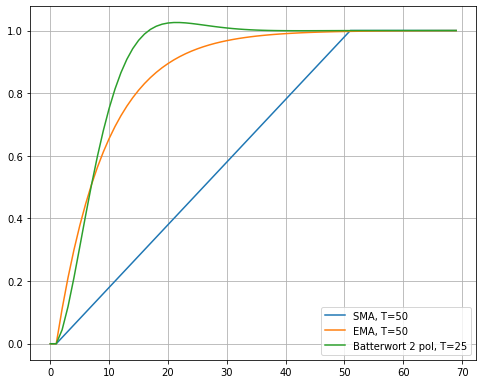
Хотите, чтобы фильтр подавлял меньше ВЧ компонент, так уменьшите период сглаживания. Сделаем период сглаживания фильтра Баттерворта Т=25, т.е. расширим полосу пропускания фильтра.
Теперь по
Ну и где разница? Групповые задержки по уровню 0.5 у ЕМА и фильтра Баттерворта стали одинаковыми, а время установления фильтра Баттерворта при одинаковых групповых задержках много лучше, чем у хваленой ЕМА. Ну, и естественно, подавление ВЧ компонент вне полосы пропускания много лучше чем у ЕМА, даже при ее Т=50.
PS Вообще-то, он пишется - Butterworth filter, но не переделывать же картинки.
Для сравнения групповых задержек различных фильтров обычно сравнивают их отклики на единичный скачок 1(t). Это, типа, ступенька высотой 1.

На рисунке сравниваются отклики на единичный скачок 2-х фильтров с периодом 50. SMA с периодом 50 приведена здесь как калибровочная.
Из рисунка можно видеть, что групповая задержка фильтра Баттерворта при одинаковом периоде Т составляет по уровню 0.5 на ~5 отсчетов больше чем у ЕМА.
Простите, а что-же вы хотели увидеть, если фильтром Баттерворта мы обрезали ВЧ часть спектра сигнала? ЕМА плохо подавляет ВЧ компоненты сигнала, отсюда и такая нервная реакция на любой чих.
Спрашивается, а зачем тогда вообще фильтр, если он мало что подавляет?
Хотите, чтобы фильтр подавлял меньше ВЧ компонент, так уменьшите период сглаживания. Сделаем период сглаживания фильтра Баттерворта Т=25, т.е. расширим полосу пропускания фильтра.

Теперь по
Ну и где разница? Групповые задержки по уровню 0.5 у ЕМА и фильтра Баттерворта стали одинаковыми, а время установления фильтра Баттерворта при одинаковых групповых задержках много лучше, чем у хваленой ЕМА. Ну, и естественно, подавление ВЧ компонент вне полосы пропускания много лучше чем у ЕМА, даже при ее Т=50.
PS Вообще-то, он пишется - Butterworth filter, но не переделывать же картинки.
3.2К |
Читайте на SMART-LAB:

AUD/USD: Флэт как пружина — покупатели защищают плацдарм для мартовского рывка
Австралийский доллар застрял в торговом коридоре. Нижняя граница в районе 0.6900–0.6940 сейчас выступает в роли фундамента, который покупатели...
22:21

Ресейл Инвест — в Топ-5 инвестиционных платформ по итогам января 2026 года
🏆 Инвестиционная платформа Ресейл Инвест вошла в пятёрку крупнейших краудлендинговых платформ по доле объёма выдач за январь 2026 года....
10:00

Корпоративные облигации
Облигации федерального займа — актив не для всех. Короткие государственные бумаги предлагают невыразительную доходность даже относительно...
16:14

Нефтяной срез: выпуск №8. Перекрытие Ормузского пролива + рост цен на нефть против слабых отчетов за 4-й квартал 2025 и 1-й квартал 2026? Ищем лучших в все еще слабом секторе
Продолжаю выпускать рубрику — Нефтяной срез. Цель: отслеживать важные бенчмарки в нефтяной отрасли, чтобы понимать куда дует ветер. Прошлый пост:...
19:45
теги блога 3Qu
- Binance
- C#
- C++
- DDE
- DLL
- EMA
- Excel
- Exponential Moving Average
- Linux
- Lua
- machine learning
- ML
- MOEX
- Moving Average
- Python
- QLua
- Quik
- Quik Lua
- Si
- Smart-lab
- SQLite
- автоматическая торговая система
- акции
- алготрейдинг
- базы данных
- Баффет
- биржа
- Боллинджер
- Брокер
- брокеры
- вероятность
- выбор
- Газпром
- гуру
- дельта
- доллар
- Доллар рубль
- доска опционов
- идеология
- инвестиции
- индикатор
- индикаторы
- интрадей
- календарный спред
- календарный спрэд
- криптовалюта
- МА
- Машинное обучение
- моделирование
- модель
- нейросети
- нейросеть
- нефть
- опрос
- опционные стратегии
- опционы
- оффтоп
- плечо
- прогнозирование
- программирование
- психология
- реклама
- роботы
- рынок
- сеточник
- скальпинг
- скользящие средние
- случайное блуждание
- смартлаб
- спекуляции
- спекуляция
- статистика
- стационарность
- стоп
- стопы
- Стратегии
- стратегия
- стрэддл
- стрэнгл
- Тейк
- терминал
- тест
- тестер стратегий
- тестирование
- технический анализ
- торговая система
- торговая стратегия
- торговые роботы
- торговые системы
- торговые стратегии
- торговый софт
- трейдинг
- ТС
- Фильтры
- Форекс
- фундаментальный анализ
- фьючерс
- фьючерс ртс
- фьючерсы
- эффективный рынок



















Сглаживающая функция должна быть гладкой, для чего у нее должны быть непрерывными хотя бы 1 производная, а лучше и больше.
У ЕМА разрывы уже в 1-й производной. Что она сглаживает?
А про ЕМА, по факту, если нет уже 1-й производной, то ЕМА немногим отличается от кусочно-линейной интерполяции на каждом отсчете, да еще и отстает.) И на фиг такое чудо нужно?
ЗЫ Хотя, понимаю.
Если играть руками, то мозги общую картину сами как-бы восстанавливают.
Если использовать какой-то доп софт для анализа, простейшие индикаторы уже не прокатывают.
Их надо просто знать и всё.
Но если мы его сглаживаем, то сглаживающая функция обязана иметь производные. Для этого достаточно всего-лишь ограничить спектр, что мы и делаем Баттервортом.
Разность двух недиффиренцируемых функций (двух ЕМА) никак не может дать в итоге дифференцируемую
Имхо, ЕМА тем и хороша, что она от всего берет понемножку. Все плоховато, но все есть.
И париться действительно ни к чему.)
Когда разберётесь с особенностями применения, тогда вам, возможно, понадобится и Баттерворт.
Это не чудо-индикатор, и без понимания зачем он конкретно нужен, он немногим лучше ЕМА.
Скажите, на практике ваши результаты от применения значительно улучшились?
Сам использую 2 КАМА (или АМА), привык уже что ли.
Однако я не возьмусь утверждать, что на стандартных индикаторах нельзя построить рабочую ТС.
Я правильно понимаю, что итоговая формула 3 порядка выглядит как
Three Poles: f = 3 g + 3(1-)f[1] — 3(1-) 2 f[2] + (1-) 3 f[3]