SMART-LAB
Новый дизайн
Мы делаем деньги на бирже
Блог им. SciFi
Расчет ожидаемого количества убыточных сделок подряд на R
- 04 мая 2016, 21:35
- |
Применим R для того, чтобы быстро посчитать, каково должно быть ожидаемое количество убыточных сделок подряд при совершении 1000 сделок.
Я написал функцию runUnluck(n) которая выдает, сколько раз мы получим n убыточных сделок подряд, если совершим 10000 экспериментов по 1000 сделок в виде подбрасывания монетки, то есть с отношением риска к доходности 1 к 1.
Здесь подробнее про функцию rle. Она как раз считает количество одинаковых исходов подряд.
Результаты:
Таким образом, если мы совершим 1000 сделок, то мы должны ожидать, что серия из 9 убыточных сделок подряд у нас хотя бы 1 раз будет.
Ожидаемое количество серий из 4 убыточных сделок подряд равно примерно 31 раз. 31 Карл!
А это гистограмма для 10000 экспериментов, 4 убыточных сделок подряд при совершении 1000 сделок.
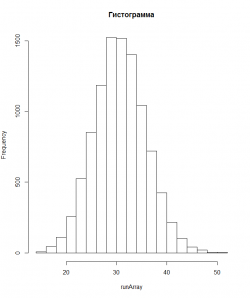
То есть в некоторых ситуациях мы получим серию из 4 убыточных сделок подряд аж 50 раз, а в некоторых меньше 20 раз. Но чаще всего будем получать около 31 раза.
Я написал функцию runUnluck(n) которая выдает, сколько раз мы получим n убыточных сделок подряд, если совершим 10000 экспериментов по 1000 сделок в виде подбрасывания монетки, то есть с отношением риска к доходности 1 к 1.
# Created by SciFi, 2016
runUnluck <- function(n) {
runArray <- numeric(10000)
for(i in 1:10000) {
runArray[i] <- sum(rle(sample(c(-1, 1), 1000, TRUE))$lengths == n)
}
hist(runArray, main="Гистограмма")
mean(runArray)
}
Здесь подробнее про функцию rle. Она как раз считает количество одинаковых исходов подряд.
Результаты:
> source("D:\\Dropbox\\R\\RunUnluck.r")
> runUnluck(6)
[1] 7.8161
> runUnluck(2)
[1] 125.2208
> runUnluck(3)
[1] 62.4047
> runUnluck(4)
[1] 31.179
> runUnluck(5)
[1] 15.6559
> runUnluck(6)
[1] 7.7635
> runUnluck(7)
[1] 3.8831
> runUnluck(8)
[1] 1.9382
> runUnluck(9)
[1] 0.9738
> runUnluck(10)
[1] 0.4922
Таким образом, если мы совершим 1000 сделок, то мы должны ожидать, что серия из 9 убыточных сделок подряд у нас хотя бы 1 раз будет.
Ожидаемое количество серий из 4 убыточных сделок подряд равно примерно 31 раз. 31 Карл!
А это гистограмма для 10000 экспериментов, 4 убыточных сделок подряд при совершении 1000 сделок.

То есть в некоторых ситуациях мы получим серию из 4 убыточных сделок подряд аж 50 раз, а в некоторых меньше 20 раз. Но чаще всего будем получать около 31 раза.
216 |
Читайте на SMART-LAB:

Станут ли алгоритмы новой нормой для частного инвестора?
ИИ всё чаще называют новой инвестиционной инфраструктурой: алгоритмы уже формируют стратегии и управляют портфелями. Каждый третий частный...
11:20

Т-Инвестиции начали аналитическое покрытие акций Аэрофлота
Аналитики Т-Инвестиции начали покрытие акций Аэрофлота. Присвоена рекомендация «держать», целевая цена – 63 рубля за акцию. ✈️ Аналитики...
12:18
теги блога SciFi
- ARIMA
- Br
- Brent
- BRN5
- ED
- EDU5
- GOLD
- HFT
- MACD
- QUIK
- Ri
- RIM6
- RiZ5
- RTS
- S&P500
- SBRF
- Si
- Si-9.15
- SiM5
- SiU5
- TSLab
- USD
- USDRUB
- акции
- алготрейдинг
- Альфа
- аналитика
- арбитраж
- бета
- Брокер
- Вариационная маржа
- Василий Олейник
- время
- Газпром
- грааль
- Гусев
- Девальвация
- деньги
- диверсификация
- Доллар
- евро
- жадность
- жизнь
- золото
- инвестирование
- инвестиции
- индекс доллара
- индикаторы
- инфляция
- ипотека
- квант
- кванты
- количественный анализ
- кукол
- курс доллара
- курс рубля
- маржин колл
- машинное обучение
- Механизм трейдинга
- ММВБ
- нефть
- Олейник
- опционы
- Открытие
- оффтоп
- портфель
- прогноз
- психология
- психология трейдинга
- рецензия на книгу
- риск
- риск менеджмент
- робот
- роботы
- РТС
- Рубль
- Сбербанк
- система
- системный трейдинг
- скальпинг
- смартлаб конкурс
- спекуляции
- среднесрок
- страх
- Талеб
- тейк-профит
- технический анализ
- Тимофей Мартынов
- торговая система
- торговые роботы
- торговый журнал
- трейдинг
- тренд
- треш
- управление капиталом
- философия
- философия трейдинга
- фьючерсы
- ЦБ
- черный лебедь




















тогда на всех надо подавать. на джаву, сишарп, джаваскрипт и пр.
и судьям то пох, они в этом не секут.
В итоге имеем:
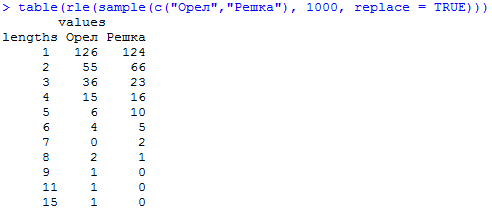
т.е. при 1000 подбрасываний монеты может быть даже 1 раз, когда 15 (!) раз подряд выпадет орел.