Коллеги, представляю результаты исследования, целью которого было определение репрезентативных (типичных) уровней доходности для основных акций российского рынка. В отличие от большинства подходов, где используется среднее арифметическое, в данном анализе в качестве метрики центральной тенденции применялась медианная логарифмическая доходность, что делает оценку более робастной к экстремальным выбросам и кризисным периодам.

Методология:
Анализ охватывает 28 голубых фишек за 10-летний период (2015-2025 гг.). Для каждой бумаги рассчитывалась логарифмическая доходность, после чего определялось её медианное значение на различных временных горизонтах (1, 3, 5 и 10 лет) и для разных масштабов агрегации данных: ежедневного, еженедельного, месячного и годового.

Ключевые выводы:

Исследование позволило установить устойчивые репрезентативные уровни медианной доходности, которые могут служить ориентиром для оценки ожидаемой доходности и риск-премии:

• На дневном масштабе: 0.0002 – 0.0007

🔍 О чем исследование?

Мы проанализировали медианную простую доходность 28 голубых фишек Мосбиржи за 10 лет (2015–2025) на разных временных горизонтах: от дневных до годовых данных. Медиана выбрана как робастная метрика, устойчивая к выбросам.

Ключевые выводы:
1️⃣ Секторальные различия:
— Финансовый сектор (Сбербанк, МКБ) лидирует на всех горизонтах: 0.06–13.97%
— Нефтегаз (Лукойл, Новатэк): до 18.19% (годовые данные)
— Металлургия и энергетика (Мечел, РусГидро): отрицательная доходность

2️⃣ Зависимость от масштаба агрегации:
— Дневная доходность: 0.02–0.07%
— Годовая: 10–18% (кумулятивный эффект)
— Привилегированные акции стабильно опережают обыкновенные (+0.2–0.5 п.п.)

3️⃣ Практическое применение:
— Калибровка моделей оценки акций
— Расчет премии за риск с учетом секторальной специфики
— Арбитражные стратегии на межвременных различиях

📊 Визуализация и методология:
В исследовании использованы:
— Ресемплинг данных (дневные → недельные → месячные → годовые)

Результаты исследования волатильности акций Мосбиржи, проведенного с использованием стандартного отклонения логарифмической доходности. Полный код и визуализации доступны в Jupyter Notebook на Kaggle.

📌 Методология
Анализ охватывает период с 2015 по 2025 год и включает:
— Расчет логарифмической доходности (log returns) для 28 голубых фишек.
— Оценку волатильности (σ) на четырех временных горизонтах: 1, 3, 5 и 10 лет.
— Агрегацию данных на дневном, недельном, месячном и годовом уровнях.
— Ранжирование акций по уровню риска с цветовой визуализацией (красный = высокая волатильность).

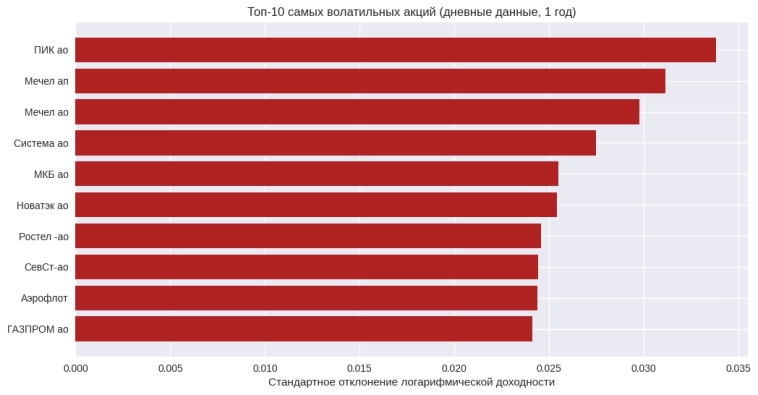
🔎 Ключевые наблюдения
1. Отраслевая стратификация:
— Максимальная волатильность: металлургия (Мечел, σ до 1.096 на годовых данных) и строительство (ПИК).
— Минимальная волатильность: энергетика (ИнтерРАО, σ = 0.014–0.049) и банки (Сбербанк).

2. Зависимость от масштаба агрегации:
— Переход от дневных к годовым данным увеличивает σ в 5–20 раз (например, для Мечела: 0.033 → 0.612).

Результаты исследования стандартного отклонения простой доходности голубых фишек Мосбиржи за 2015-2025 гг. Это продолжение нашей серии анализов рыночного риска.

📌 Методология:
— Рассчитано стандартное отклонение простой доходности (%)
— Временные горизонты: 1, 3, 5 и 10 лет
— Масштабы агрегации: дневной, недельный, месячный, годовой
— Визуализация через цветовую градацию (красный = высокий риск)

🔎 Ключевые выводы:

1. Секторальный анализ риска:
— Металлургия (MTLR/MTLRP) — лидер по волатильности на всех горизонтах
— Энергетика (IRAO) и нефтегаз (LKOH) — наиболее стабильные сектора
— Четкое разделение на 3 кластера риска (высокий/средний/низкий)

2. Масштабирование риска:
— Дневное стандартное отклонение: 1.5-3.5%
— Недельное: 3.0-8.5% (+120-150% к дневной)
— Месячное: 7-20% (в 2.5-3 раза выше недельной)
— Годовое: 30-165% (на порядок выше месячной)

3. Аномалии:
— IRAO показала уникальный скачок риска на 10-летнем горизонте (80.17%)
— Нелинейный рост риска при увеличении временного горизонта

💡 Практическое применение:

В рамках анализа российского рынка акций проведено исследование средней логарифмической доходности 28 голубых фишек Мосбиржи за 10-летний период. Эксперимент охватывал различные временные горизонты (1, 3, 5, 10 лет) и масштабы агрегации данных (ежедневный, еженедельный, месячный, годовой). Методология включала расчет логарифмических доходностей, ресемплинг данных и сравнительный анализ с цветовой визуализацией результатов. Особое внимание уделялось выявлению репрезентативных уровней доходности по секторам, которые могут служить ориентиром для количественных стратегий и оценки риск-премии.

Результаты показали:

• Финансовый сектор (Сбербанк) и нефтегазовые компании (Лукойл, Новатэк) демонстрируют устойчивость на всех горизонтах

• Металлургия (Мечел, ММК) и розничный сектор (Магнит) — максимальную волатильность

• Долгосрочные (10-летние) доходности большинства эмитентов остаются положительными

Подробная аналитика с интерактивными таблицами и методологией доступна в Kaggle-ноутбуке:

В таблице представлены средние дневные простые доходности 28 голубых фишек за разные периоды. Лидеры по доходности — Сбербанк (0.06-0.14%), Аэрофлот (0.13%) и Новатэк (0.11%), тогда как Магнит (-0.11%) и РусГидро (-0.07%) показывают отрицательные значения. Особый интерес представляет цикличность Мечела: низкие показатели за 1 год (-0.14%), но сильный рост за 5 лет (+0.09%).

Полный анализ с таблицами для недельной, месячной и годовой доходности доступен в Kaggle-тетрадке: https://www.kaggle.com/code/eavprog/moex-avg-simple-returns-ranking. Данные могут быть полезны для сравнения стратегий и оценки риск-доходности.

Переход от дневной волатильности к недельной, месячной, годовой или произвольному окну делается с помощью масштабирования стандартного отклонения (волатильности) по корню из количества периодов.

Если известна дневная волатильность, чтобы получить волатильность за T дней, её нужно умножить на знак корня из T.
Формула:
волатильность_Тдней = волатильность_дня × √T

Обратный переход: если дана годовая волатильность, чтобы получить дневную, её нужно разделить на √252, где 252 — среднее число торговых дней в году.

Примеры:
— Недельная волатильность = дневная × √5
— Месячная волатильность = дневная × √21
— Годовая волатильность = дневная × √252

Или наоборот:
— Дневная волатильность = годовая ÷ √252

Это работает, если доходности независимы и одинаково распределены (в реальности не всегда так, но формула используется очень часто).

Для других периодов используйте эту же логику, просто подставляя нужное количество дней.