Добрый вечер!
В продолжение темы https://smart-lab.ru/blog/612608.php, хотелось бы добавить небольшое исследование.

Итак, мы остановились на том, что приращения рыночных котировок представляют собой расстояния, которое проходит броуновская частица за экспоненциальное время.
Еще раз смотрим на интегрированный процесс по таким приращениям:

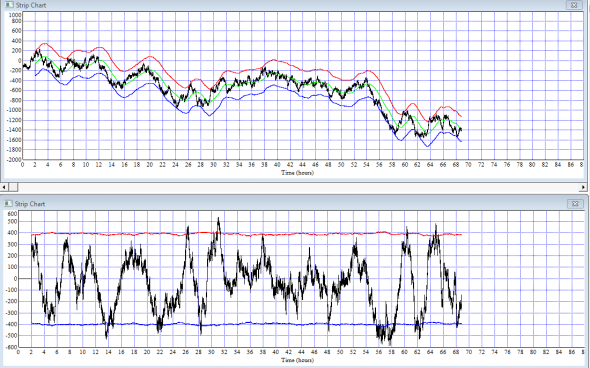
Хорошая модель, но… Не хватает главного — ответа на вопрос: а откуда берется нестационарность дисперсии реального рыночного процесса?
Ведь дисперсионный канал ±(sqrt(2*D*t)) на нижнем графике суммы приращений в скользящем временном окне практически =const, а на деле: 


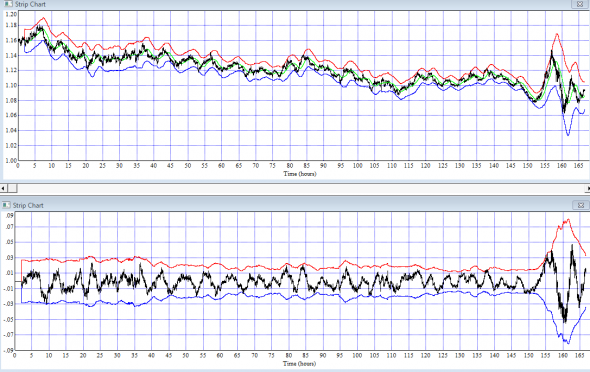
( Читать дальше )

Господа!
Искренне надеюсь, что среди вас есть программисты.
Прошу, как говорится, войти в положение… Не всем же дано шарить в искусстве кодирования на каких-то инопланетных языках.

Вопрос: как из тикового архива в формате .csv, взятого, к примеру, с Дукаскопи, сделать такую вещь, по столбцам:

1. День недели (0, 1, 2, 3, 4, 5, 6)

2. Час

3. Минута

4. Секунда

5. Bid

6. Ask

7. Бит (0/1) принадлежности к реальной или псевдокотировке

Заполнены должны быть все строки таблицы посекундно. Т.е. за сутки должно сформироваться ровно 86400 строк таблицы.

Очень важно — если не было в данную секунду реальной котировки, записывается предыдущее значение.
В столбце 7 прописываем бит = 1, если котировка реальная, 0 — если псевдокотировка (т.е. предыдущее значение)

Может, есть уже у кого-нибудь готовый макрос для Excel? Али какая-нибудь программа? 
Если ни у кого ничего нет — скиньте хотя бы алгоритм, как это делать.

В обмен — будущий Грааль. А?

С уважением,
Toddler.

Грааль...  Где ж ты находишься?
Иногда мне кажется, что Он рядом, только руку протяни, ан — нет, не все так просто. Но, жажда напиться из Него — безмерна. Продолжим наш путь.

Сегодня постараемся смоделировать распределение приращений цены. Ведь мы же помним, что оно выглядит вот так:


( Читать дальше )

Продолжаем наш нелегкий путь к познанию рынка.

Се ля ви… Нам надо, во что бы то ни стало, найти Грааль. Мы верим, что на рынке немарковский процесс, процесс с памятью, когда цена зависит от всех предыдущих своих значений или, по меньшей мере, от значений внутри временных циклов рынка.

А как же марковская модель? Применима ли она к рынку? Не в том ли проблема, что мы уверены, что будущие значения цены зависят только от текущего значения цены и ее скорости, а все предыдущие значения отказываемся принимать в расчет — ведь в этом смысл модели Маркова, не так ли?

Для ответа на этот вопрос, нам потребуется рассмотрение уравнение Фоккера-Планка (или прямого уравнения Колмогорова). Оно выводится для системы хаотически движущихся (броуновских) частиц, т.е. диффузионного облака молекул.
В общем случае, оно выглядит так:

  

( Читать дальше )

Предисловие.
Иногда читаю наиболее интересные посты смартлабовцев… Естественно, не мог не обратить внимание на изыскания Бориса Гудылина — неповторимый слог, аура, поэзия рынка. Кажется — еще шаг, полшага и вожделенный Грааль падет в руки страждущих. Ключевым моментом его исследований является видения рынка как совокупности петель гистерезиса, образуемых ценой. Но, так ли это упрощает задачу изъятия наличных с рынка и переадресации их в свой собственный карман?

Немарковская парадигма рынка
Собственно — сразу к делу.
То, что Б.Гудылин узрел гистерезис на ценовом графике, сразу наталкивает на мысль — а какими же уравнениями описывается собственно это явление?
Поискав по книгам, можно найти ответ на этот вопрос.
Конечно же, интегро-дифференциальными уравнениями типа:

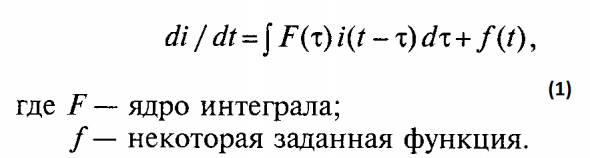
Понятно, что данное уравнение чрезвычайно трудно решаемо без знания ядра F. Именно поэтому рынок вызывает крайнюю сложность в понимании, но оставляет надежду трейдерам. Ведь всем и каждому становится понятно, что каждое значение цены в настоящем и будущем предопределено всей ее историей. А значит технический анализ на основании исторических архивов имеет право на жизнь. Все что было в прошлом обязательно повторится.

( Читать дальше )

В продолжение темы:
https://smart-lab.ru/blog/608175.php
хочется сказать следующее.

Раз уж удается разложить исходное распределение приращений цены

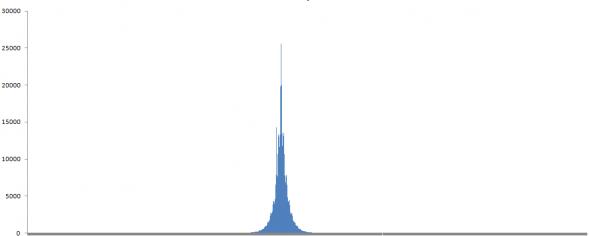
на двойное треугольное:


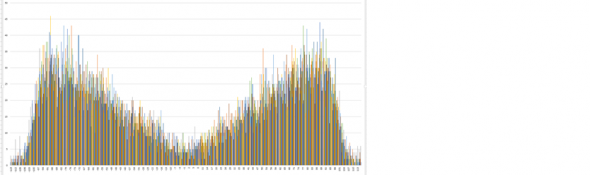
( Читать дальше )

Доброго времени суток, господа!

М-да… Вся лента забита новостями: коронавирус, нефть-матушка, кризис...

А где же будоражащие душу исследования, напрямую ведущие к Граалю? Нетути… Нетути Грааля аль, все ж таки, есть?

Продолжим путешествие в мир случайности/закономерности рыночных временных рядов с целью узреть Свет и Счастие для всех страждущих.
В предыдущих частях проекта:
https://smart-lab.ru/blog/579572.php
https://smart-lab.ru/blog/580961.php
https://smart-lab.ru/blog/582407.php
мы убедились, что заработать на теоретических случайных процессах («монетка», Laplace motion, ...) довольно просто. Пользуемся тем фактом, что сумма независимых или слабозависимых случайных величин (приращений) дает число, принадлежащее нормальному распределению Гаусса и при выходе текущей кумулятивной суммы за пределы диапазона +-Delta*1.96, где Delta = sqrt(2*(b^2)*t), заключаем сделки, а при возврате в 0 — закрываем их. Дело сделано...

( Читать дальше )

Пожалуй, настало время рассмотреть рыночный ВР более подробно.

Почему он гораздо сложнее пресловутой «монетки»? Как вообще такое может быть, что на обычном случайном блуждании мы спокойно зарабатываем, а на рынке ничего не получается? Откуда берутся гигантские импульсные движения цены?

Для попытки ответа на эти вопросы, в первую очередь мы рассмотрим распределение вероятностей приращений (первых разностей цены) CLOSE M1 для пары EURUSD за 2018 г.
Оно всем известно и загадочно. Выглядит оно вот так:


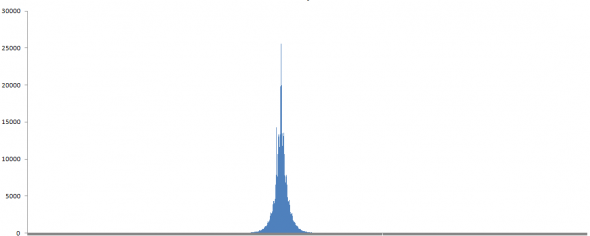
Еще никому не удалось понять — почему оно такое, островершинное и тяжелохвостое. Откуда оно взялось и как его смоделировать?
Постараемся ответить на эти вопросы. Не сейчас, не быстро, но, думаю у нас это получится.

В первую очередь попробуем аппроксимировать его обычным (обычным ли?) треугольным распределением.
Совсем простым — как сумму двух равномерно распределенных величин. Как будто бросаем 2 монетки (ведь мы же помним, что Волшебник говорил, что на рынке мы видим суперпозицию именно двух процессов, не так ли?) и два полученных результата просто суммируем.

( Читать дальше )

Продолжение.
Начало здесь - https://smart-lab.ru/blog/579572.php

В прошлый раз мы рассмотрели метод, дарованный свыше, применительно к случайному блужданию.
Уважаемые трейдеры моментально побежали применять его к рынку и… тут же выразили свое недовольство, что он не работает. :)))
«Сомнения рождают страх, страх рождает ненависть...» — так в народе говорят, что ли?
Я тоже сомневаюсь — честно говоря, никогда не пробовал ранее его в деле. Ну, давайте посмотрим.
Минуя исследования гауссовских и лапласовских случайных процессов, побегу-ка я, сломя голову, исследовать реальный рыночный ВР.

Рассмотрим пару EURUSD с 01.01.2019 по 08.12.2019 на ценах закрытия CLOSE M1 
Выборка данных = 349716 значений, скользящее окно = 7200 (как и в эксперименте для «монетки»).

Конечно, рыночный ВР сложнее и говоря о применимости соотношения Sigma*sqrt(T) для вычисления стандартного отклонения процесса, прежде всего необходимо научиться правильно вычислять Sigma. Для «монетки» Sigma=1. А для рыночного ВР?

( Читать дальше )

Добрый день, господа!
Начиная серию публикаций о способе заработка на случайных процессах и, в частности, на классическом случайном блуждании (т.н. «монетке»), я преследую одну цель — дать возможность трейдерам переосмыслить свои взгляды на рынок.
Поехали!
Итак, первым экспериментом будет «монетка». Да-да, обычный random walk — суммирование приращений +1 и -1, вероятность выпадения которых на каждом шаге итерации = 50/50.
Выборка данных = 349716 значений (сделано это для исследования работоспособности предлагаемого метода заработка на паре EURUSD с 01.01.2019 по 08.12.2019 на ценах закрытия CLOSE M1, которое будет произведено позднее).
Выглядит случайное блуждание так:


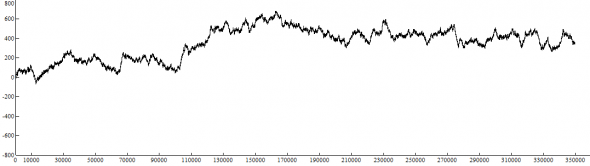
Считается, что на таком процессе невозможно заработать. Так ли это?
Воспользуемся методом скользящей кумулятивной суммы приращений.
Выберем скользящее окно данных = 7200 значений, что соответствует недельному скользящему окну по EURUSD на ценах закрытия CLOSE M1.

( Читать дальше )