SMART-LAB
Новый дизайн
Мы делаем деньги на бирже
Блог им. Toddler
Как заработать на случайном блуждании. Часть 2
- 14 декабря 2019, 13:14
- |
Продолжение.
Начало здесь - https://smart-lab.ru/blog/579572.php
В прошлый раз мы рассмотрели метод, дарованный свыше, применительно к случайному блужданию.
Уважаемые трейдеры моментально побежали применять его к рынку и… тут же выразили свое недовольство, что он не работает. :)))
«Сомнения рождают страх, страх рождает ненависть...» — так в народе говорят, что ли?
Я тоже сомневаюсь — честно говоря, никогда не пробовал ранее его в деле. Ну, давайте посмотрим.
Минуя исследования гауссовских и лапласовских случайных процессов, побегу-ка я, сломя голову, исследовать реальный рыночный ВР.
Рассмотрим пару EURUSD с 01.01.2019 по 08.12.2019 на ценах закрытия CLOSE M1
Выборка данных = 349716 значений, скользящее окно = 7200 (как и в эксперименте для «монетки»).
Конечно, рыночный ВР сложнее и говоря о применимости соотношения Sigma*sqrt(T) для вычисления стандартного отклонения процесса, прежде всего необходимо научиться правильно вычислять Sigma. Для «монетки» Sigma=1. А для рыночного ВР?
Для решения этого вопроса перепишем формулу для стандартного отклонения процесса в следующем виде:
Delta = sqrt(D*t) (1),
где D — дисперсия распределения вероятностей рыночных приращений цены.
t — время
Смотрим на графики пары EURUSD с 01.01.2019 по 08.12.2019 и на сумму приращений в скользящем недельном окне = 7200:
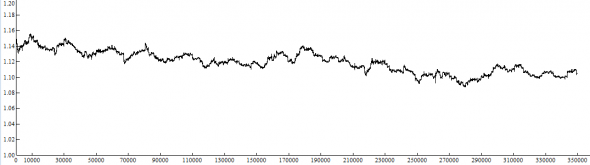
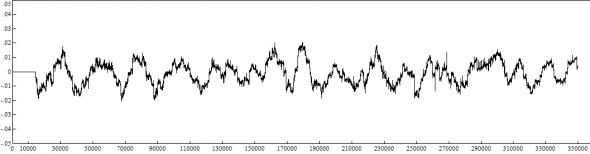
Нас, конечно, интересует нижний график.
Образует ли набор сумм 7200 рыночных приращений распределение Гаусса? Каково стандартное отклонение этого распределения?
Гистограмма:
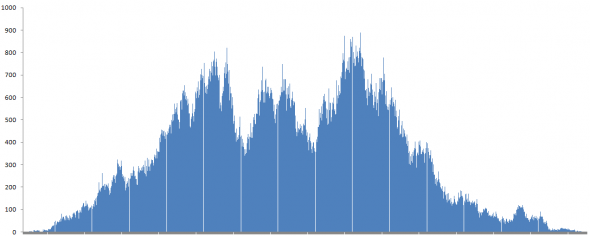
Статистика:

В определенном смысле — да, перед нами опять нормальное распределение.
Крайне важно теперь вычислить дисперсию D из соотношения (1).
… долгие вычисления...................................................
:))) Не буду мучить уважаемых читателей. Это знание дали мне Волшебники и оно гласит, что
D = 2*(b^2) (2),
где b — среднее арифметическое значение модуля приращения рыночного ВР.
Это соотношение характерно для всех случайных гамма-процессов.
Т.о стандартное отклонение процесса на нижнем графике:
Delta = sqrt(2*(b^2)*t) (3),
Построим теперь график суммы приращений с двусторонним доверительным 95%-й интервалом +-Delta*1.96
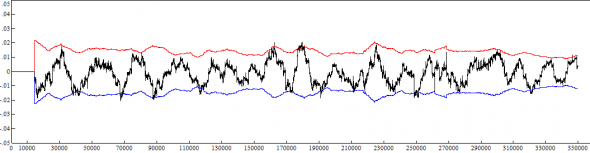
Стратегия:
При выходе за верхнее значение доверительного интервала (за красную линию) заключаем сделку SELL
При выходе за нижнее значение доверительного интервала (за синюю линию) заключаем сделку BUY
Выход из сделки при возврате скользящей суммы в 0.
И хотя входы/выходы производятся по графику скользящей суммы, сами сделки фиксируем по графику EURUSD.
Результаты:

Видим, что из 16 проведенных сделок — 13 в плюс, 3 — в минус. Общий профит = 5612 пункта по пятизнаку.
Честно — я ошеломлен результатами эксперимента...
Продолжение следует?
Не знаю… Мне надо посоветоваться и получить разрешение.
Дополнение
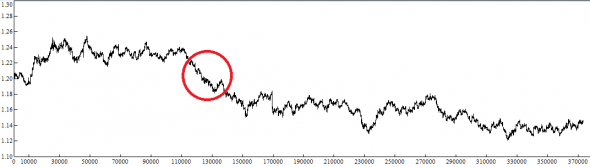
Провел исследования на паре EURUSD с 01.01.2018 по 31.12.2018 на ценах закрытия CLOSE M1
Выборка данных = 373444 значений, скользящее окно = 7200 (как и ранее).
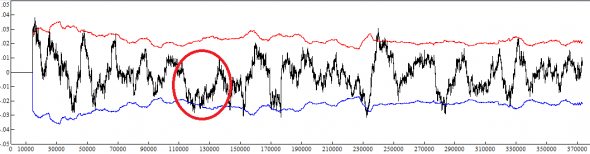
Смотрим на графики самой пары и на сумму приращений в скользящем недельном окне:
Результаты:

Да, за 2018 год результаты хуже — всего +1367 пункта по пятизнаку и при одной крайне неудачной сделке (выделена красными кружками на графиках и таким же цветом в таблице).
Но, все равно — прибыль есть!
Впереди еще долгий-долгий путь исследований и страданий....
Спасибо за внимание.
Начало здесь - https://smart-lab.ru/blog/579572.php
В прошлый раз мы рассмотрели метод, дарованный свыше, применительно к случайному блужданию.
Уважаемые трейдеры моментально побежали применять его к рынку и… тут же выразили свое недовольство, что он не работает. :)))
«Сомнения рождают страх, страх рождает ненависть...» — так в народе говорят, что ли?
Я тоже сомневаюсь — честно говоря, никогда не пробовал ранее его в деле. Ну, давайте посмотрим.
Минуя исследования гауссовских и лапласовских случайных процессов, побегу-ка я, сломя голову, исследовать реальный рыночный ВР.
Рассмотрим пару EURUSD с 01.01.2019 по 08.12.2019 на ценах закрытия CLOSE M1
Выборка данных = 349716 значений, скользящее окно = 7200 (как и в эксперименте для «монетки»).
Конечно, рыночный ВР сложнее и говоря о применимости соотношения Sigma*sqrt(T) для вычисления стандартного отклонения процесса, прежде всего необходимо научиться правильно вычислять Sigma. Для «монетки» Sigma=1. А для рыночного ВР?
Для решения этого вопроса перепишем формулу для стандартного отклонения процесса в следующем виде:
Delta = sqrt(D*t) (1),
где D — дисперсия распределения вероятностей рыночных приращений цены.
t — время
Смотрим на графики пары EURUSD с 01.01.2019 по 08.12.2019 и на сумму приращений в скользящем недельном окне = 7200:


Нас, конечно, интересует нижний график.
Образует ли набор сумм 7200 рыночных приращений распределение Гаусса? Каково стандартное отклонение этого распределения?
Гистограмма:

Статистика:

В определенном смысле — да, перед нами опять нормальное распределение.
Крайне важно теперь вычислить дисперсию D из соотношения (1).
… долгие вычисления...................................................
:))) Не буду мучить уважаемых читателей. Это знание дали мне Волшебники и оно гласит, что
D = 2*(b^2) (2),
где b — среднее арифметическое значение модуля приращения рыночного ВР.
Это соотношение характерно для всех случайных гамма-процессов.
Т.о стандартное отклонение процесса на нижнем графике:
Delta = sqrt(2*(b^2)*t) (3),
Построим теперь график суммы приращений с двусторонним доверительным 95%-й интервалом +-Delta*1.96

Стратегия:
При выходе за верхнее значение доверительного интервала (за красную линию) заключаем сделку SELL
При выходе за нижнее значение доверительного интервала (за синюю линию) заключаем сделку BUY
Выход из сделки при возврате скользящей суммы в 0.
И хотя входы/выходы производятся по графику скользящей суммы, сами сделки фиксируем по графику EURUSD.
Результаты:

Видим, что из 16 проведенных сделок — 13 в плюс, 3 — в минус. Общий профит = 5612 пункта по пятизнаку.
Честно — я ошеломлен результатами эксперимента...
Продолжение следует?
Не знаю… Мне надо посоветоваться и получить разрешение.
Дополнение
Провел исследования на паре EURUSD с 01.01.2018 по 31.12.2018 на ценах закрытия CLOSE M1
Выборка данных = 373444 значений, скользящее окно = 7200 (как и ранее).
Смотрим на графики самой пары и на сумму приращений в скользящем недельном окне:


Результаты:

Да, за 2018 год результаты хуже — всего +1367 пункта по пятизнаку и при одной крайне неудачной сделке (выделена красными кружками на графиках и таким же цветом в таблице).
Но, все равно — прибыль есть!
Впереди еще долгий-долгий путь исследований и страданий....
Спасибо за внимание.
5.6К |
84 комментария
вопрос, возможно, глупый, но задам для точности восприятия: ВР — это временной ряд?
- 23 апреля 2020, 18:26

Toddler, Здравствуйте! А можно узнать, куда подевались все комментарии?
- 24 апреля 2021, 21:00

Читайте на SMART-LAB:
Разруливаем год Делимобиля в шоу «Акционеры. Цифры»
Провели эфир с топ-менеджерами оператора каршеринга — компании Делимобиль. Узнали из первых уст взгляд на финансовые результаты бизнеса за...
16:40





















