Блог им. EkaterinaKutnyak
Как вести учет облигаций в Excel. Расчет доходности
- 05 декабря 2023, 22:14
- |
Часть 2
Расчет доходности
Рада, что предыдущий пост про НКД понравился. По поводу всевозможных сторонних сервисов для учета ценных бумаг и анализа портфеля. Я, конечно, ничего не имею против. Лишь бы этот учет был. Я все же предпочитаю вести портфели сама, чтобы не зависеть особо от сторонних ресурсов и чтобы, это самое главное, видеть те характеристики портфелей, которые необходимы для принятия тактических и стратегических решений.
Ну, а сейчас, к расчету доходности.
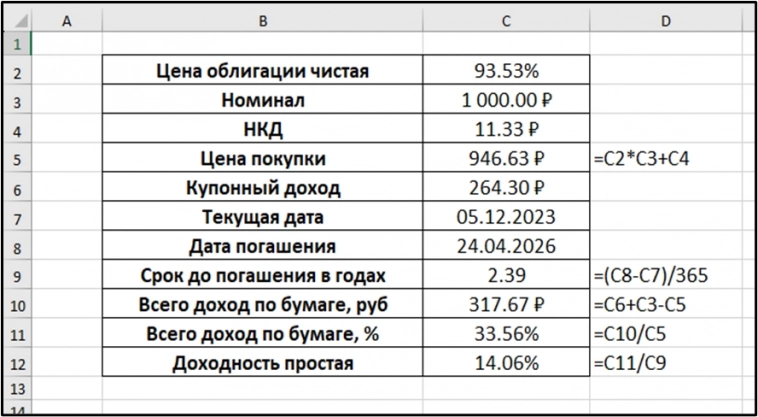
Самая простая и понятная по смыслу доходность – это простая доходность к погашению. Рассмотрим все ту же облигацию Уральской стали.
Для расчета доходности нам потребуется график купонных выплат. Где его взять? Он есть, например, на Smart-lab. Есть он и на сайте биржи.
По бумаге предстоит получить еще 10 купонов по 26.43 руб. Итого 264.3 руб.
Кроме этого, нам нужна цена облигации. Мы ее закачаем с биржи, используя формулу: =ПОДСТАВИТЬ(@ ФИЛЬТР.XML(ВЕБСЛУЖБА(«iss.moex.com/iss/engines/stock/markets/bonds/boards/TQCB/securities/»&B3&"/securities.xml?iss.meta=off&iss.only=securities&securities.columns=SECID,PREVLEGALCLOSEPRICE");"//document//data//rows//row/@PREVLEGALCLOSEPRICE");".";".")
Где В3 – это ячейка с ISIN.
Сейчас цена облигации ниже номинала. Значит при погашении мы получим прибыль от прироста стоимости.
Теперь у нас есть все, чтобы рассчитать простую доходность к погашению.
Простая доходность к погашению, в отличие от эффективной доходности к погашению, не учитывает тот факт, что купоны можно реинвестировать.
Если рассматривать российский рынок, а он у нас очень «короткий» по мировым меркам, то простая доходность нам куда полезнее.
Но общепринятое правило, сравнить облигации, используя эффективную доходность к погашению. То есть с учетом возможного реинвестирования купона.
Не хотелось бы перегружать пост лишними формулами, но, одну использовать придется.
Для того, чтобы определить эффективную доходность к погашению, начинать надо с того, как формируется цена облигации. Цена облигации — это сумма всех денежных потоков, приведенных (дисконтированных) к текущему моменту.
Где
C – размер купона в год (Номинал облигации * ставку купона)
n – количество купонных выплат в год
N – номинал облигации
T – количество периодов до погашения
t – текущий период
Значение r в этой формуле – эта та самая доходность к погашению, которая нам нужна. А цена у нас есть. Это рыночная стоимость.
Посчитаем эффективную доходность для Уральской стали. Поток платежей уже есть. Просто немного модифицируем его. Помним, что в конце вместе с купоном мы получим и номинал. А покупая облигацию сегодня, заплатим текущую стоимость и НКД (накопленный купонный доход).
Когда известны даты выплат купонов, идеальной функцией для поиска эффективной доходности к погашению является ЧИСВНДОХ.
Это функция привязана к датам и подходит для расчета внутренней ставки доходности, чем и является эффективная доходность.
В этой функции всего два аргумента: поток платежей по бумаге (С2: С12) и даты выплат (В2: В12). То, что мы платим вбиваем со знаком «минус».
И наконец, для тех, кому считать совсем не хочется. Доходность тоже можно закачать, используя ссылку: =ПОДСТАВИТЬ(@ ФИЛЬТР.XML(ВЕБСЛУЖБА(«iss.moex.com/iss/engines/stock/markets/bonds/boards/TQCB/securities/»&B3&"/securities.xml?iss.meta=off&iss.only=marketdata&marketdata.columns=SECID,YIELD");"//document//data//rows//row/@YIELD");".";"."). Где В3 ячейка с ISIN.
И да, доходность к погашению можно посчитать только в том случае если известен поток платежей. А это постоянный и фиксированные купоны. При переменном купоне доходность считают к оферте. Если купон плавающий, то этот показатель не имеет смысла.


теги блога Ekaterina Kutnyak
- Excel
- p/e
- акции
- Альфа-Банк
- валюта
- вероятности
- дивиденды
- доходности облигаций
- дюрация
- замещающие облигации
- Итоги недели
- Книги
- мнения
- мультипликаторы
- НКД - накопленный купонный доход
- обзор рынка
- облигации
- оферта
- оферта миноритариям
- оферта по облигациям
- Портфель инвестора
- психилогия
- психологические ошибки
- расчет
- расчёт риска
- рецензия на книгу
- риск
- рынок
- ставка рефинансирования
- трейдинг
- учет портфеля
- флоатеры




















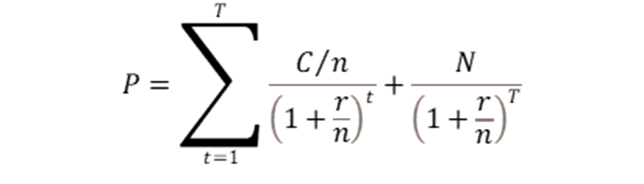


Я как-то считал ручками — совпало.
За формулу спасибо, не знал, я уж хотел макрос писать.
Вот только при нынешних движениях курса доходность становится неактуальной и нужно вносить поправку к цене от вчерашнего курса
=ФИЛЬТР.XML( ВЕБСЛУЖБА("https://iss.moex.com/iss/engines/stock/markets/bonds/boards/TQCB/securities/"&B3&"/securities.xml?iss.meta=off&iss.only=securities&securities.columns=SECID,PREVLEGALCLOSEPRICE"); "//document//data//rows//row/@PREVLEGALCLOSEPRICE" ) спасибо дипсику подправил для меня формулу