Блог им. Gusan
Эмпирическое распределение
- 10 января 2017, 23:01
- |
Интересную тему с эмпирическими распределениям подняли Дмитрий Новиков и Nonsense. Хотелось бы одну мысль по этому поводу озвучить. Насколько понимаю, эмпирическое распределение — это когда берут историю цен БА, нарезают неким окном, из каждого полученного отрезка получают приращение, и потом строят частотную диаграмму из этих приращений. Полученное распределение и называют эмпирическим. Nonsense пишет, что возникают две проблемы:
1. У полученного распределения мю может быть не ноль, и если считать по этому распределению справедливые цены, то не будет выполняться колл-пут паритет.
2. Выбор размера окна для нарезки.
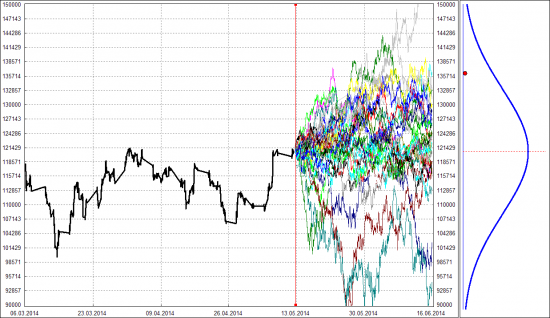
Мне же кажется, что тут другая, более существенная, проблема. Предположим, у нас есть некий случайный процесс, с помощью которого мы можем сгенерировать кучу случайных траекторий цены:
Построив частотную диаграмму финишных точек каждой траектории, мы получим как-бы распределение вероятностей — истинное для нашего случайного процесса. Теперь вопрос: если мы возьмем только одну траекторию и построим из нее эмпирическое распределение, будет ли оно совпадать с истинным распределением? Уверен, что нет.
Анализируя одну такую траекторию может быть и можно частично понять некоторые св-ва исходного случайного процесса (типа, рост волатильности при падении цены), но полностью его расшифровать — мне кажется, невозможно.
И еще соображение. Мы ведь говорим про вероятности. А что это? Так понимаю, есть два подхода: частотный и байесовский. И вроде бы второй подход гораздо точнее прогнозирует (например, тот кто прогнозирует будет сегодня дождь или нет на основе кол-ва дождливых дней в году проиграет тому, кто смотрит ясный сегодня день или пасмурный). Так вот, эмпирическое распределение соответствует частотной вероятности. А рыночное распределение (получаемое из текущих цен опционов на всех страйках) — байесовскому подходу. Например, выходит какая-то важная новость, рыночное распределение на это сразу реагирует и соответствующим образом изменится. А эмпирическое никак на эту новость не отреагирует.
В общем, использовать эмпирическое распределение (для прогноза где будет БА или для подсчета своих справедливых цен), имхо, дюже неправильно.






















1. Откуда возникает улыбка
2. Модель Хестона и гэпы
Вот допустим, наша система прогнозирования сообщает, что с вероятностью 60% цена вырастет, а с 40% — упадет. Достаточно ли этого для принятия торгового решения, покупать или продавать фьюч?
1. с вер-тью 60% следующее приращение будет +10п, 40% что будет -10п.
2. 60%: +10п, 40%: -20п.
В первом случае МО = +1п, во-втором = -1п. Т.е. в первом случае нужно покупать, во втором — продавать. Причем в каждом случае будет свое OptF (доля счета, на которую оптимально открыться, это ведь тоже важный вопрос). Оба варианта отличаются именно распределением вероятностей, где будет цена на следующем приращении. Т.е. получается, даже для линейной торговли (голым фьючом), очень полезно знать все распределение (а не только вероятность вырастет или упадет). И уж тем более это полезно для торговли опционами. А вы утверждаете, что это никому не нужно...
Волатильность БА в основном влияет на второй момент распределения вероятностей, но есть и третий (асимметрия) и четвертый (толщина хвостов, вер-ть гепов) и т.д. Как вы объясните одной только волатильностью БА, что у Si третий момент положителен (дно улыбки слева от текущ БА), а у Ri — наоборот?
нормальное подбиралось по равенству дисперсии?
А если ему уменьшить дисперсию, не станет ли оно более точно аппроксимировать гистограмму?
я не знаю, как по науке сравнить типы распределений, поэтому и спросил :) в учебниках тоже этого вопроса не встречал (кажется).
Интуитивно, я бы делал так: распределения различаются формой, поэтому для сравнения формы надо максимально аппроксимировать одну кривую к другой. Критерий любой, например МНК. Можно уменьшить веса хвостов, т.к. для них мало значений, и в этих областях точность аппроксимации ниже.
«отличие в хвостах будет уже наверное на порядок.» — так это же хорошо (наверное), ведь это одно из главных различий, которые мы ищем.
После аппроксимации я бы разделил гистограмму на подогнанную кривую, и тут хвосты визуально проявились бы во всей красе)))
Насчет неточности прогноза, мне понравилось у него:
Припоминаю, он приводил там статистику за последние 100лет, что несмотря на все сложности прогноза погоды, землетрясений и т.д. — точность прогнозов все-таки постепенно растет.
Насчет байесовского подхода, имел ввиду, что вероятность это не что-то фиксированное и абсолютное (как предполагается в частотном подходе), а очень субьективное и постоянно меняющееся. Когда есть априорная вероятность события A, потом происходит событие B, и можно пересчитать апостериорную вер-ть P(A|B) по формуле Байеса.
В отношении восстановления случайного процесса по некоторой реализации — чисто чёрный ящик вы не восстановите никогда. Необходимо знать хотя бы что-то об исследуемом процессе. Под это дело обычно подбирается некоторая модель, а дальше MLE/QMLE, CSS и другие методы позволят по данным реализации получить оценки параметров модели.
С точки зрения построения прогнозов лучшим в смысле СКО является условное мат.ожидание Y_{t}.
Прокомментирую.
Когда вы сравниваете прогноз погоды 1) на основе частотного подхода и 2) байесовского, вы немного лукавите.
Фактически вы сравниваете анализ приращений погоды и абсолютного значения погоды. А на самом деле оба прогноза будут исходить из текущей погоды (солнце за окном или дождь). Да, у абсолютного значения погоды есть инерция. Т.е. если сейчас солнце, то очень вероятно, что и через полчаса будет солнце. Но! Изменение погоды в течение этих получаса — вот о чем речь — как его вы будете анализировать байесовским подохдом? По идее, если бы были ставки на погоду, можно было бы вернуть вероятности из коэффициентов выплаты (по аналогии как вы делаете на опционах). Но фактически с рынком есть 2 большие разницы:
1. на рынке сами ставки (на опционах) влияют на цены базовых активов. Погода же полностью живет по своим правилам.
2. применение байесовского подхода подразумевает большую волатильность волатильности + значительную волатильность матожидания. Первый же подход основывается на статичности рядов.
Мне кажется, П2 будет точнее прогнозировать. Разве нет?
сейчас температура 10 градусов
П1 посчитал, что из 1000 исходов на день из предыдущих периодов в это же время года, матожидание изменения темп-ры за день будет пол градуса, а СКО, скажем, 2.5%. При этом он не учел текущий тренд (для этого нужно было бы взять, скажем, только 20 последних исходов). Вот он и делает прогноз: 11 градусов, диапазон 8,5-13,5 градусов.
П2 делает так: смотрит в окно и видит, что прошла бабуся, вся укутанная в шубу и из мерседеса вылез парень в ветровке и в футболке. Для примера берем малое количество инфы (что соответствует низкой ликвдности на опционах, все что не ри и не си). П2 все это усредняет и делает вывод, что температура будет х градусов. Т.е. второй аналитик основывается не на объективных данных, а на мнениях других индивидов, которые, очевидно, переработали большое количество информации, и рискуют своим здоровьем (деньгами в случае с опциями) в случае неправильной оценки.
как то так