Блог им. uralpro
Модель скрытых состояний Маркова. Часть 1
- 12 мая 2015, 14:35
- |
В данном цикле статей начинаем рассматривать модель Маркова, которая находит применение в задачах классификации состояния рынка и используется во многих биржевых роботах. Статьи основаны на постах, опубликованных в блоге Gekko Quant. Также будет рассмотрены практические алгоритмы на финансовых рынках. Код в цикле приведен на языке R. Вначале будет много теории, ее надо хотя бы попробовать понять, затем разберем практические примеры.
Рабочая среда распознавания основных паттернов.
Рассмотрим набор признаков O, полученный из набора данных d и класс w, обозначающий наиболее подходящий класс для O:
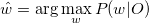
Так как P(w|O) неизвестен, применяем правило Байеса:
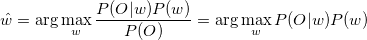
Максимизация не зависит от P(O), поэтому мы можем игнорировать эту вероятность. P(O|w),P(w) означают вероятность того, что данные O принадлежат классу w и вероятность существования класса w соответственно.P(O|w) определяется моделью скрытых состояний Маркова.
Формулировка задачи.
Сначала нам нужно сгенерировать набор признаков О из рыночных данных d. Пока пропустим этот шаг, потому что он будет различаться для разных применений модели Маркова, например для финансов d может быть представлен ценами разных активов и О можно обозначить набор технических индикаторов, применяемых к d. Модель Маркова также популярна в задачах распознавания речи, где О обычно является вектором, описывающим характеристики частотного спектра речи.
Затем необходимо вектор О ассоциировать с классом модели Маркова. Это можно сделать путем применения метода максимального правдоподобия, где модель Маркова определяет класс, который с наибольшей вероятностью генерирует набор параметров, соответствующий набору параметров О.
Спецификация модели Маркова.
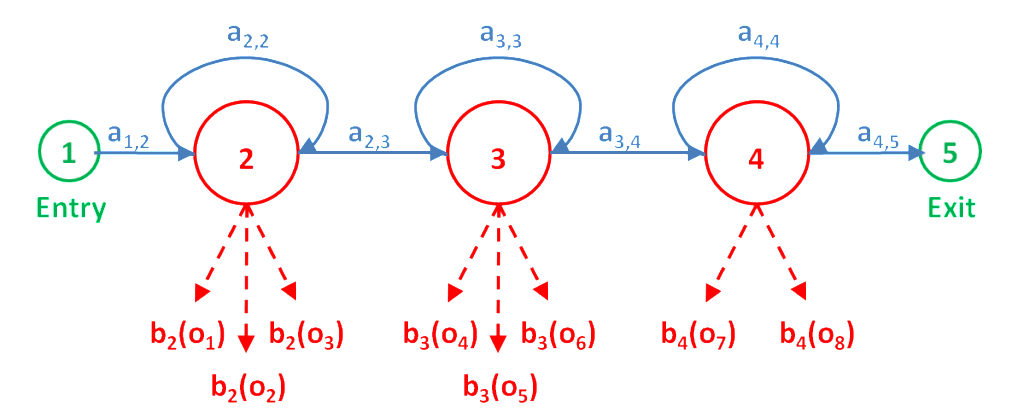
Рассмотрим рисунок в заглавии поста. На нем приведены следующие обозначения:
N — число состояний модели (на рисунке равно 5),
ai,j- вероятности перехода из состояния i в состояние j,
bj(O)- вероятность получения вектора параметров О при состоянии j ( j не является входным и выходным состоянием),
вектор параметров модели Маркова λ определим как ![Модель скрытых состояний Маркова. Часть 1 \lambda=[N,a_{i,j},b_j]](http://mathurl.com/mtqzz2r.png) ,
,
![Модель скрытых состояний Маркова. Часть 1 O=[o_1,o_2,...,o_T]](http://mathurl.com/k4skrbw.png) — вектор параметров наблюдений,
— вектор параметров наблюдений,
![Модель скрытых состояний Маркова. Часть 1 X=[x_1,x_2,..,x_T]](http://mathurl.com/lt7m9qs.png) — найденный вектор последовательности состояний.
— найденный вектор последовательности состояний.
Совместная вероятность соответствия вектора О последовательности состояний X при параметрах модели λ равна вероятности перехода из текущего состояния в следующее, умноженное на вектор параметров, сгенерированный в этом состоянии:
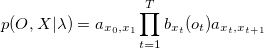
где x0,xT+1- входное состояние 1 и выходное соcтояние N соответственно.
Вычисление вероятности.
В рассмотренной выше совместной вероятности мы определили последовательность состояний X. Так как эта последовательность является скрытой переменной ( вот почему модель Маркова называется моделью скрытых состояний), мы ее не знаем. Однако, если мы суммируем вероятности по всем возможным состояниям, то получим:
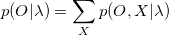
Это может быть проблематичным из-за большого числа состояний модели (особенно в приложениях реального времени), но существуют эффективные алгоритмы для такого вычисления, без нахождения каждого отдельного состояния. Подобным алгоритмом является форвардный алгоритм.
Что представляет из себя bj(o)?
Это полученное распределение вероятностей при состоянии j модели. Это распределение может быть любым, но оно должно соответствовать распределению данных при состоянии j, и должно быть математически определяемым. Обычным выбором на этой стадии является предположение, что вектор O может описываться набором гауссовских распределений — мультивариантным нормальным распределением. В качестве предупреждения отметим, что если составляющие вектора параметров сильно коррелированы между собой, тогда Σ- ковариационная матрица — будет иметь много вычисляемых значений. В этом случае нужно подбирать вектор парметров так, чтобы Σ представляла собой диагональную матрицу, другими словами, параметры не должны быть кореллированы между собой:
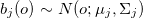 , где μ,Σ- параметры мультивариантного гауссовского распределения.
, где μ,Σ- параметры мультивариантного гауссовского распределения.
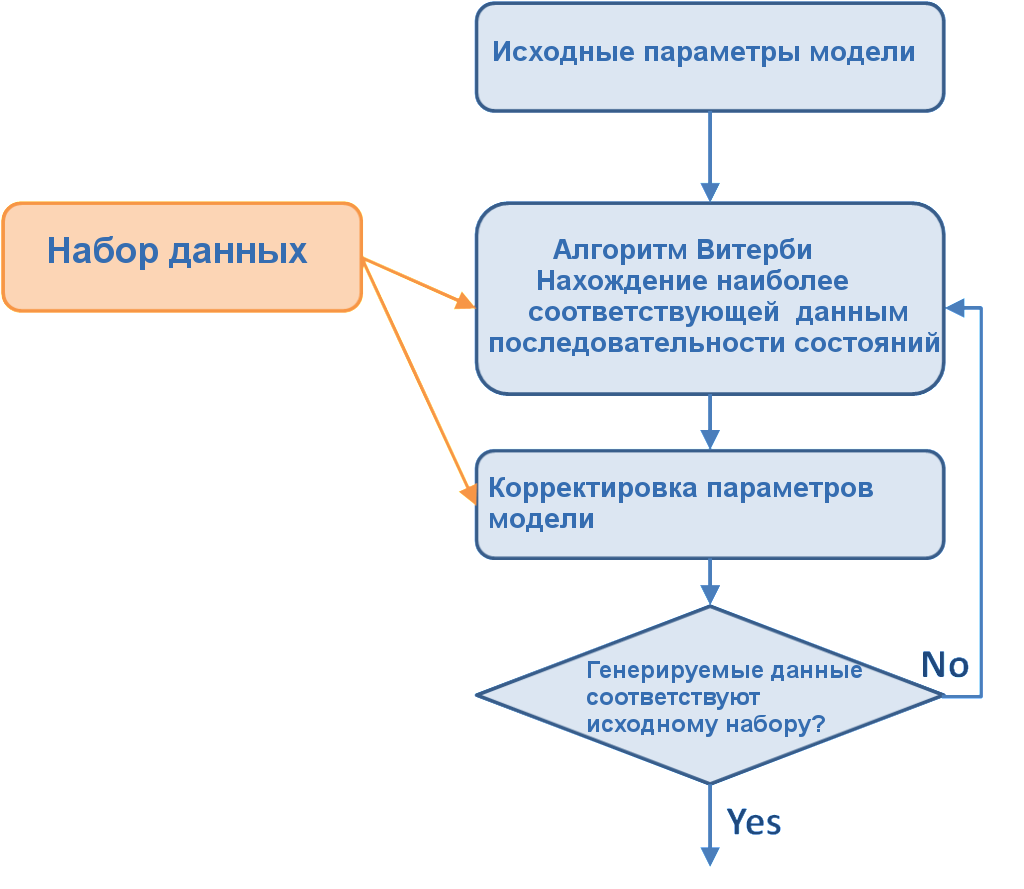
Как получить bj(o)? Определение параметров методом Витерби.
Мы знаем, что для описания нормального распределения достаточно методом максимального правдоподобия вычислить среднее распределения μ и ковариацию Σ вектора параметров. Значит мы должны получить только среднее и ковариацию вектора параметров для состояния j нашей модели, используя так называемую сегментацию Витерби. Она подразумевает нахождения жесткого соответствия между вектором параметров и последовательностью состояний, которое его генерировало. Существует также и альтернативный метод Баума-Вельша, который ассоциирует вектор параметров с несколькими последовательностями состояний с определенной вероятностью.
Состояние j генерирует наблюдения, начиная с tj:
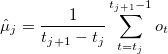
![Модель скрытых состояний Маркова. Часть 1 \hat{\Sigma}_j=\frac{1}{t_{j+1}-t_j}\sum_{t=t_j}^{t_{j+1}-1}[(o_t-\hat{\mu}_j)(o_t-\hat{\mu}_j)^{`}]](http://mathurl.com/phl9ofv.png)
Наперед неизвестно, какая последовательность какой вектор наблюдений генерирует, но существует алгоритм Витерби, позволяющий решить эту проблему с некоторым приближением:
Подробно алгоритм Витерби, а также форвардный алгоритм для эффективного вычисления p(O|λ) рассмотрим в следующей части.
Другие стратегии, применяемые в алгоритмической торговле и биржевых роботах смотрите в моем блоге и на сайте.
теги блога uralpro
- ARIMA
- data feed
- ETF
- FORTS
- GARCH
- HFT
- IQFeed
- mean reversion
- momentum
- python
- S&P500
- VIX
- VPIN
- алгоритм
- алгоритм торговли
- алгоритмическая торговля
- алгоритмы
- алгоритмы торговли
- алготрейдинг
- альфа-сигналы
- андрей мовчан
- Биржевые роботы
- биткоины
- Блэк-Шоулз
- бэктестинг
- возврат к среднему
- волатильность
- высокастотники
- высокая доходность
- высокочастотная торговля
- высокочастотный трейдинг
- генетические алгоритм
- генетические алгоритмы
- гэп
- доходность трейдеров
- импульс
- импульсная система
- индексы
- интервью
- итоги
- итоги 2016
- Итоги 2018
- книга заявок
- коинтеграция
- колокейшн
- Конференции смартлаба
- конференция
- корреляция
- криптовалюта
- лчи
- маркет дата
- маркет мейкер
- марковиц
- марковский процесс
- математические модели
- машинное обучение
- модели
- Модели рынка
- модель
- модель Маркова
- Оптимизация портфеля
- опционные модели
- опционы
- Парный трейдинг
- парный трейдинг
- подготовка данных
- поток ордеров
- Публикации
- публикация
- разработка алгоритма
- разработка торговых систем
- раундтрип
- регрессия
- результат торговли
- робот
- роботы
- роботы в биржевой торговле
- скользящая средняя
- стакан
- стоп лосс
- стратегия
- торговля волатильностью
- торговые алгоритмы
- торговые стратегии
- улыбка волатильности
- ФОРТС
- Херст
- эквити
- язык R



















оказываецца как все просто то и тривиально...
— мои щи сложнее намного
У меня к Вам вопрос, без подвоха, действительно хочу знать Ваш мнение. Если без формул, что дает Вам уверенность, в том что найденные закономерности устойчивы? Как объяснить владельцу кирпичного завода, что под стратегию можно давать деньги (по моему опыту люди легко понимают факторы на товарных рынках, а с мат. моделями намного сложнее)? Не кажется ли Вам, что основой торговой системы является ММ, а фильтр сделок — мат. модель или какие-то примитивные правила — не так важны? Спасибо.
Закономерности устойчивы как раз потому, что имеют четкое математическое или статистическое обоснование. Если вы понимаете, как работает модель на уровне мат. закономерностей, вы легко определите, как они меняются во времени и изменение торгового алгоритма станет почти автоматической процедурой. Что вы имеете в виду под ММ? Если манименеджмент, то это важная, но не определяющая часть алгоритма. Все-таки самое главное — это положительное мат. ожидание стратегии. Которое можно оценить большим количеством испытаний — то есть статистически. Поэтому бессмыслены всякие стратегии, где вывод делается на основании, скажем 30 сделок за год, это все статистически недостоверно. А если брать историю за 20 лет — это тоже не вариант, слишком мало взаимосвязей на таких промежутках времени ( если конечно, там не было постоянного тренда, как в Америке). Поэтому столь привлекательны HFT алгоритмы, где за один или несколько дней набирается достаточная статистика.
Сука, я не понял ни одного предложения, как такая ебанина с формулами может иметь что-то общее с заколачиванием бабла на рынке?))))
Абсолютно никакой. Рынок одна из тех сфер, в которых чистая математика даёт полностью оторванные от реальности результаты. Ценой на рынке движет ценообразование, что есть непрерывный процес оценки стоимости актива участниками. В один момент оценка одна, в другой момент-другая. Оценка может меняться мгновенно. Именно оценка стоимости определяет то, за сколько продавцы желают продать и насколько с этим согласны покупатели. Единственным индикатором оценки стоимости актива является её цена, а динамикой изменения оценки актива является
динамика изменения цены. И тут не нужно ничего сложнее стандатных всем известных индикаторов, основанных на анализе цены. Объёмы тоже не играют никакой роли в ценообразовании, так как показывают только то, что в какой-то момент в прошлом сошлись такое-то количество покупающих и продающих, и этот факт на динамику ценообразования в будущем никак не влияет, цена может бегать не только без объёмов, но и вообще без котировок, если изменится оценка цены участниками. Крупные игроки используют алгоритмы в торговле, но ни в коем случае не для того, чтоб предсказать рынок, это невозможно. Алгоритмы используются, например, для продажи большого объёма без изменения цены вниз, или скупка без роста цен. Именно эти алгоритмы создают краткосрочные тренды (несколько дней), в которых крупные игроки занимают позиции, например на нисходящем краткосрочном тренде, крупняк закупается.