Копипаст | Мат.ожидание или "Теория казино"

Принято считать, что основной товар в казино — это адреналин. Часто мы слышим, что казино предлагает вытянуть «счастливый билет», много реже говорят что казино продает сервис. На самом же деле, основной товар казино — это азарт от возможности выигрыша. В этой статье мы рассмотрим основные принципы, на которых организована работа игорных домов, обоснование прибыли заведения, и какую роль в ее деятельности играет «госпожа удача». 

А начнем обзор с рассмотрения основных математических законов, на которых построены азартные игры. Как связаны математика и казино? Ведь все игры в казино были придуманы и разработаны именно математиками. Можно ли использовать их же оружие для получения преимущества в игорном доме? 

Математика игр казино 

Рассмотрим процессы, происходящие в азартных играх, с точки зрения теории вероятности, и попробуем определить, подчиняются ли игры казино математике. 

Бросая монету, можно утверждать, что любая из ее сторон может выпасть с одинаковой вероятностью. Есть всего две возможности — выпадет либо орел, либо решка. Вероятность того, что при бросании монеты выпадет решка равна? (50%), то есть мы вправе ожидать, что в половине случаев будет выпадать решка. Часто говоря о вероятности употребляют слово шанс. Шанс на то, что при броске монеты она упадет решкой вверх, равен 50% 

Вероятность показывает, как часто ожидаемый нами результат может быть достигнут, и может быть представлена как отношение ожидаемых исходов к общему количеству всех возможных исходов за достаточно продолжительный период времени при большом количестве повторений. 

Математическое ожидание при игре в рулетку 

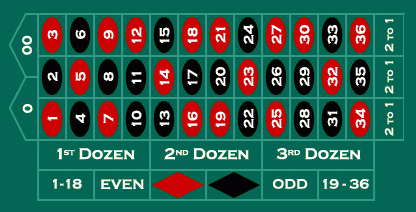
Рассчитаем математическое ожидание при игре в рулетку (американская версия с двумя секторами «зеро» ноль и двойной ноль) при ставке 5$ на цвет (черное): 18\38 х (+5$) + 20\38 х (-5$) = -0,263 

Как вы уже наверное заметили, в обоих приведенных примерах, величина математического ожидания имеет знак «-», что характерно для большинства ставок казино. Отрицательное математическое ожидание на практике означает, что, чем дольше длится игра, тем больше вероятность проигрыша для игрока. 

Перевес казино (House Edge) [доля заведения] – величина, противоположная математическому ожиданию игрока и показывающая, какой процент от ставок, сделанных в процессе игры за определенный промежуток времени, удерживается в пользу казино.Сейчас мы будем рассматривать самый популярный вид игры в казино, знаете какой? Самая популярная игра казино во всем мире — это игра в рулетку.Перевес казино в европейской рулетке составляет 1 — 36/37 = 2,7%, в американской рулетке уже 1 — 36/38 = 5,26% (за счет двух зеро). Это означает, что, если вы, играя в рулетку, за определенное время поставили в общей сложности 1000 долларов, то велика вероятность, что в конечном итоге около 27$ (европейская рулетка) и 54$ (американская рулетка) пойдет в доход игорному заведению. В настольных играх перевес казино меньше (Баккара, Блэкджек или Крэпс), поэтому шансы выиграть в них выше. 

В качестве примера посчитаем, каковы наши шансы в казино при игре в американскую версию рулетки, игровое колесо которой, напомню, насчитывает 38 секторов (1-36 цифры + 2 сектора зеро). Предположим, что мы поставили на число. Оплата выигрыша, в этом случае производится в соотношении 1 к 36 

Вероятность выиграть в этом случае 1\38 или 2,63% 
Возможный выигрыш игрока (в процентах к ставке): 1/38 х 36х100 = 94.74% 
Процент казино: 100 – 94,7 = 5.26 % 
Математическое ожидание: [(1\38) х 36 (+1)] + [(37\38) x (-1)] = -0,0263 
То есть, с каждого поставленного вами доллара, игорный дом надеется заработать 2,63 цента. Другими словами математическое ожидание выигрыша игрока при игре в американскую рулетку в казино составляет -2.6% от каждой вашей ставки. 

Выводы: 

Не надо быть великим математиком, чтобы играть в казино. Можно даже не считать математическое ожидание и дисперсию — это сделали до вас и можно пользоваться готовыми результатами. Главное понимать, что игры, имеющие большую величину математического ожидания, выгоднее для игрока, так как в них преимущество казино перед вами меньше и, соответственно, время вашей игры и возможная сумма выигрыша увеличивается. Ищите игры, в которых реализовано преимущество игрока, только в этом случае вы можете рассчитывать на выигрыш в достаточно долгой игре. 

При выборе рулетки отдавайте предпочтение европейскому варианту (с одним «зеро») так как в ней преимущество казино будет 2,7%, в отличии от американской версии (с двумя «зеро»), в котором перевес игорного заведения равен уже 5,26%. 

Но, рассуждая о положительных и отрицательных математических ожиданиях, вы не должны забывать и о том, что существует дисперсия. И чем она выше, тем больше вас будет «лихорадить» в игре. Вы будете проигрывать в играх с преимуществом игрока, и, в то же время, можете выиграть там, где казино имеет значительный перевес математического ожидания. Помните, что вся математика азартных игр казино корректно работает только в случае, когда число попыток велико и, поэтому, достигнуть на практике расчетных ожидаемых величин достаточно сложно из-за ограниченности бюджета игрока, величины ставок или времени игры.

Источник[1];
Отдельная благодарность Алексею Маркову и его книге "Хулиномика".
Именно из за него и его творения побудилась идея создания данной статьи.