SMART-LAB
Новый дизайн
Мы делаем деньги на бирже
Информация
Блог им. Kot_Begemot
Случайности в волатильности и эффективные оценки
- 21 июня 2020, 20:34
- |
Используя простые модели волатильности, рассчитанные по ценам закрытия (Close-to-Close vol.) мы неизбежно сталкиваемся с рыночным шумом, смещающим наши оценки далеко её от истинного или асимптотического значения. Мы могли бы измерять волатильность как-то иначе, например по модели Паркинсона (High-to-Low 1980), но столкнулись бы с той же проблемой.
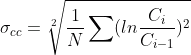
1.1 — Close to Close log-volatility estimation
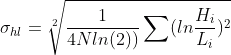
1.2 Parkinson (High to Low) log-volatility estimation
Эти две оценки волатильности, хоть и являются случайными числами, но используют совершенно различную информацию ({Close} и {High,Low}). На первый взгляд ничего интересного, но Garman и Klass, воспользовавшись теоремой Цыбенко (Neural Net approximation), решили построить на базе этих двух случайных чисел, новое, более эффективное случайное число, собрав, всего-навсего, из них простой, непараметрический портфель.
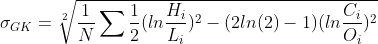
1.3 Garman and Klass log-volatility estimation
Математики заявляют, что этот портфель в семь с половиной раз эффективнее старой-доброй Close-to-Close.
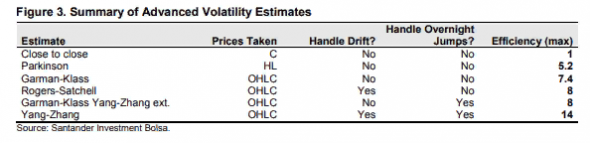
Сравнительная эффективность методов оценки волатильности.
Ну вот это мы сейчас и проверим!
Возьмем Gaussian Normal Standart Noise, построим из него Japan Candle graph, и начнем к нему EWMA 10 estimation применять!
Matlab:
q=10000; w=10; x=randn(q,w)/w^0.5;
x=cumsum(x,2); OLHC=zeros(q,4);
for i=1:q;
OLHC(i,2)=min([0,x(i,:)]);
OLHC(i,3)=max([0,x(i,:)]);
OLHC(i,4)=x(i,w);
end;
clear x q w i;
>> OLHCs=OLHC+cumsum([0;OLHC(1:end-1,4)])*ones(1,4);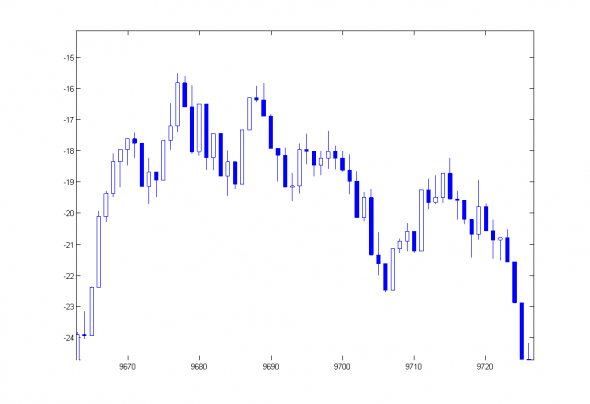
Matlab Random Candle Noise with truth unit volatility = 1.
Matlab:
volcc=tsmovavg(OLHC(:,4).^2,'e',10,1).^0.5; volcc(1:10)=[]; volhl=(1/4/log(2))^0.5*tsmovavg((OLHC(:,3)-OLHC(:,2)).^2,'e',10,1).^0.5; volhl(1:10)=[]; volhl=volhl/mean(volhl); volgk=tsmovavg( 0.5*(OLHC(:,3)-OLHC(:,2)).^2 - (2*log(2)-1)*OLHC(:,4).^2 ,'e',10,1).^0.5; volgk(1:10)=[]; volgk=volgk/mean(volgk);
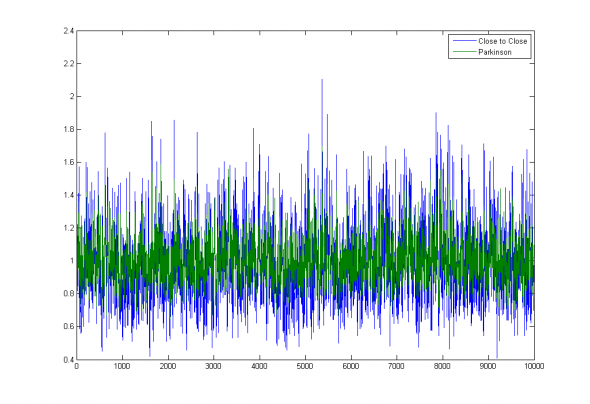
Close-to-Close estimation error = 0.22, Parkinson estimation error = 0.13;
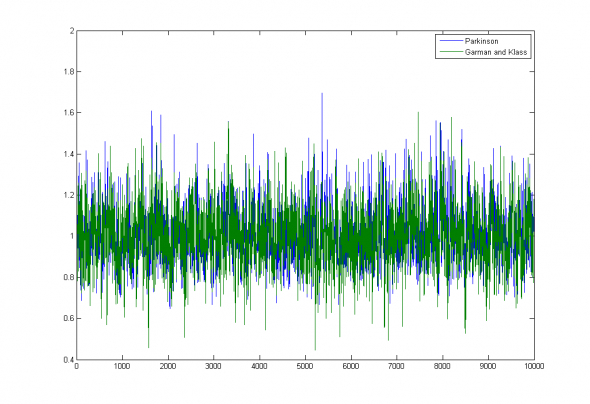
Parkinson estimation error = 0.13, Garman and Klass estimation error = 0.135; (преимущество Garman and Klass наблюдается на окнах >20)
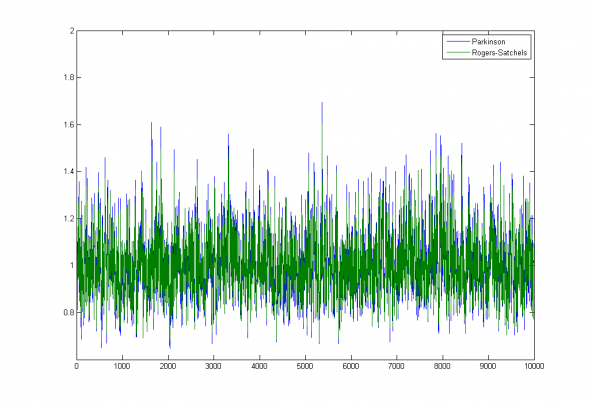
Parkinson estimation error = 0.13, Rogers-Satchell estimation error = 0.12;
Неправильные какие-то математики получились, ненормированные. Надо опять к Бабе Яге идти, она эти волатильности… ух как умеет!
теги блога Kot_Begemot
- API
- cpp
- FORTS
- LUA
- Matlab
- NASDAQ
- open source
- Quik Lua
- S&P
- S&P500
- S&P500 фьючерс
- Vanguard Group
- VIX
- акции
- акции США
- алгоритмы
- алготрейдинг
- анализ временных рядов
- баффет
- волатильность
- Гордон
- доверительное управление
- долги
- игры
- инвестиции
- индекc
- интеграция
- искусственный интеллект
- Келли
- Книги
- книги о трейдинге
- корреляция
- кризис
- криптовалюта
- лудомания
- Марковиц
- матлаб
- машинное обучение
- ММВБ Акции
- наука
- нейронные сети
- облигации
- одураченные случайностью
- оптимизация
- оптимизация торговых систем
- опционы
- оффтоп
- оционы
- памм счета инвестиции
- паника
- пирамида
- ПИФы
- портфели
- Портфель
- портфельное инвестирование
- пузыри
- раздача
- рецензия
- Риски
- рэнкинг мосбиржи
- Сбербанк
- спекуляции
- статистика
- стоимостное инвестирование
- талеб
- теги не нужны
- теория игр
- торговая система
- торговые роботы
- трейдинг
- улыбка волатильности
- управляющая компания
- финанализ
- фундаментальный анализ
- фьючерс ртс
- Шарп
- шутка
- Экономика
Вы меня переплюнули, снимаю шляпу! Браво!
Например у нас есть последовательность 1, 2, 3, 4 — как видно, смещение равно 1, т.е. максимальная разница между этими величинами. Как её посчитать? Если всё сложить и разделить на количество, получим 2.5 — не круто, это нам не о чем не говорит (хотя это нам говорит о мат. ожидании).
Но нам интересно получить разброс. Если просто взять каждое значение и сравнить его с МО, сложить и получить среднее, получим 1 — что есть среднее абсолютное отклонение (MAD). Но это значение выходит не очень информативным, т.к. его можно получить из разных величин с гораздо меньшим разбросом, например (1, 1, 2 = 1 или 1.5, 0.5, 0.5, 1.5 = 1 и т.д.).
Чтобы исправить это мы и используем квадраты (СКО). Так мы получаем разницу МО минус значение, в квадрате, потом сумму квадратов делим на количество и извлекаем корень. Итого имеем относительно точное значение разброса. Для 1, 2, 3, 4 получим 1.25. Не 1, но близко. Это и есть волатильность.
(в случае чего, на истину в первой инстанции не претендую, сохраняю право на ошибку)
написал внизу про волатильность.
ЗЫ вообще, всю обработку реал-там инфы в прямоугольных окнах давно не делают.
В обработке сигналов так не делают. А они, в большинстве своем, стационарны.
Увеличьте выборку, и все дела.
Получается примерно так.
Это индикаторы волатильности, но не совсем то, что вам надо.
Зы. А чтоб не оч увеличивался там надо окно, что-то типа e^(-x^2), и можно начать где-то с середины интервала.
Зы2 Или даже куском синуса окно завершить.
Вы так говорите, как буд-то сумма x(i) это не есть самая простая линейная (или даже нулевая) аппроксимация, лишь волей случая совпадающая с МОЖ. А какая-нибудь сумма S1(x) и S2(x) не есть какая-то нейронная сеть на каких нибудь… квадратичных нейронах.
какое-то самозапутывание… и чем займней выглядит тем больше видимо в него веришь и запутываешься :)))
Существует два определения:
1) Волатильность рыночная, она же историческая, она же реальная — сие есть расчет или прикидка на глаз амплитуды колебаний конкретного инструмента. Акция волатильная — значит хорошо ходит, можно делать деньги. Акция сильно волатильная — значит шлак, который делает резкие значительные и плохо просчитываемые движения. Из-за повышенного риска сильную волитильность (амплитуды на графике) рекомендутся избегать.
Пункт 1) и 2) никак не связаны. Хотя слово «волатильность» в них одно и то же.
2) Волатильность вменённая, она же подразумеваемая, она же надуманная, она же предполагаемая, она же будущая волатильность, она же IV (ай-ви), она же сигма == это аналог выражения «цена опционов», аналог выражения «премия опционов», аналог выражения «риск опционов».
Левая и правая часть этого смыслового предложения (до и после знака ==) железно связывается формулой Блека-Шоулза. Это единственное предназначение формулы. Для этой формулы мы используем или цену опциона (реальную или придуманную) и получаем волатильность в процентах. Или задаем волатильность в процентах (реальную или придуманную) и получаем цену опционов. Поэтому тут стоит знак равенства. Чаще придуманную, чем реальную. Потому что цены для опционов мы берем «из общих соображений», с потолка. И кто-то на них соглашается, проходит сделка. Вот и всё.
Выражение трейдера с торгового деска «Я продал волатильность» означает, что он выставил опционы на продажу по хорошей спекулятивной цене, взятой с потолка, и у него их купили.
Выражение «Я продал волатильность» (в опционах, для акций не катит) равносильно «Я двинул лохам опционы по хорошей цене. Включаем счетчик временного распада и съедаем риск на завтрак!»
Обычное словоблудие. Ничего сложного.
человек выше спрашивал