Глобальные оценки инвестиций - стресс-тест и адекватная оценка риска (численный эксперимент).

     В задачах оценки бизнес проектов, прогнозирования спроса, определения справедливой цены опциона или портфельного инвестирования, так или иначе, возникает проблема адекватной оценки рисков.  Обычно за риск принимается простое, выборочное среднеквадратичное отклонение, для которого хорошо разработан аппарат математической статистики, позволяющий прогнозировать критические показатели, например просадки,  и проводить стресс-тесты в предположении центральной предельной теоремы, то есть в предположении узкой стационарности  наблюдаемых процессов.

     Однако, мы зачастую имеем дело с абсолютно  другими, нестационарными процессами. Не стационарность процесса может быть вызвана  как нелинейным синергетическим эффектом  (реклама и «сарафанное радио»,  мода, политические выборы, революции и пр. самоорганизации),  как множественностью состояний системы (тренд/флэт), так и просто  некоторой инерцией системы, связанной, например, с задержкой принятия решений основными игроками.

(Это когда на рынок влияет некоторое событие, например освоение новой технологии  или выпуск нового товара, но рынок оценивает его не сразу, а постепенно, инерционно, не успевая за изменениями.)

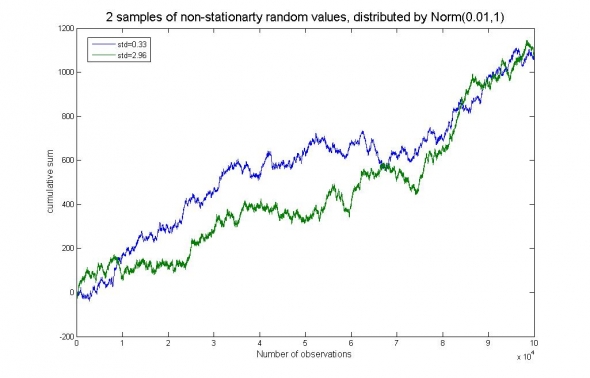
Рис. 1. Моделирование случайной величины с разным откликом на управляющие воздействие, сохраняющей, при этом, глобальные статистические показатели Еv=0.01, Std.=1, соответственно статистическим показателям событий.

Несмотря на то, что два ряда «распределены» по Гауссу (обладают глобальным поведением соответствующим Гауссу) с математическим ожиданием 0.01 и среднеквадратичным отклонением равным единице, выборочная оценка риска этих двух рядов далека от 1 – для ряда «устойчивого» она составляет 0.33, то есть риск занижен в три раза, а для ряда «активного»  (например, постоянно тестирующего, ищущего справедливую цену) – завышен в 3 раза до 2.96.

Иными словами, в случае невыполнения ограничений, накладываемых центральной предельной теоремой, оценки дисперсии по выборочным данным являются глобально-неадекватными (несмотря на собственную устойчивость) и не пригодными для проведения стресс-тестов.  Не удивительно, что финансисты и экономисты часто прибегают к разного рода мракобесию, выдумывая малопонятные надстройки и извращения «честных» математических методов (то же коэффициент Сортино по отношению к коэффициенту Шарпа).

Тем не менее, зная (или верно предполагая) природу не-стационарности  исследуемых процессов, можно успешно получить их глобальные характеристики (пригодные для проведения стресс-тестов). Приведём пример временного ряда статистик 2-ого порядка, рассчитанных для стационарного и не-стационарно-инерционного ряда, двумя различными алгоритмами – с учётом инерционности и без:

 
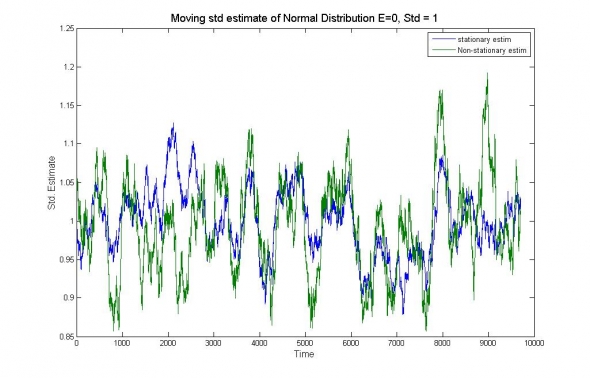
Рис.2. Оценка среднеквадратичного отклонения стационарного временного ряда распределённого по Гауссу (0,1).  Синяя кривая – стандартная оценка, зелёная кривая – с поправкой на инерцию.

      Как видно, для оценки стационарных процессов, стандартный алгоритм оценки (выборочная дисперсия) работает несколько лучше (его преимущество нивелируется с ростом размера выборки).

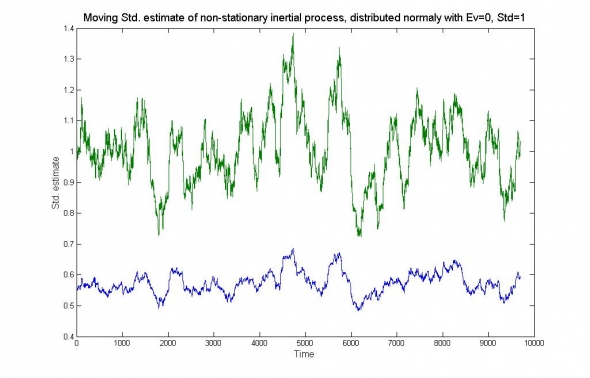
Рис.3. Оценки нестационарного (в данном случае инерционного) временного ряда со стандартным отклонением 1. Синяя кривая – стандартная оценка, зелёная – оценка с поправкой на не-стационарность.