SMART-LAB
Новый дизайн
Мы делаем деньги на бирже
Блог им. SerSer
Индикатор фрактальной размерности | LUA
- 07 октября 2016, 15:50
- |
Упрощенный алгоритм вычисления приближенного значения размерности Минковского, для ценового ряда.
Краткая справка:
Размерность Минковского — это один из способов задания фрактальной размерности ограниченного множества в метрическом пространстве, определяется следующим образом:Размерность Минковского имеет так же другое название — box-counting dimension, из-за альтернативного способа ее определения, который кстати дает подсказку к способу вычисления этой самой размерности. Рассмотрим двумерный случай, хотя аналогичное определение распространяется и на n-мерный случай. Возьмем некоторое ограниченное множество в метрическом пространстве, например черно-белую картинку, нарисуем на ней равномерную сетку с шагом ε, и закрасим те ячейки сетки, которые содержат хотя бы один элемент искомого множества.Далее начнем уменьшать размер ячеек, т.е. ε, тогда размерность Минковского будет вычисляться по вышеприведенной формуле, исследуя скорость изменения отношения логарифмов.
- где N(ε) минимальное число множеств диаметра ε, которыми можно покрыть исходное множество.
Более полная и интересная статья
Ну а я применил данный алгоритм, для создания простого индикатора фрактальной размерности
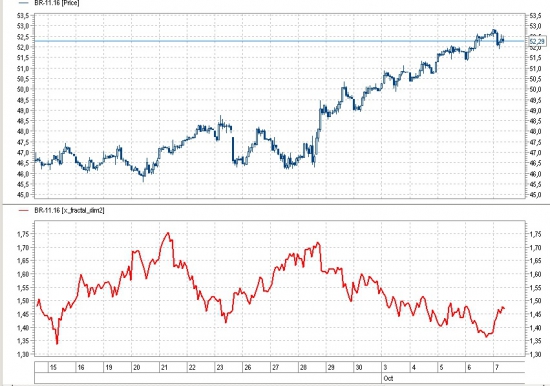
Для чего? — как альтернативный индикатор определения состояния в тренде или во флете.
Для сравнения
Размерность простой линии = 1
Размерность множества Жулиа (картинка выше) = 1,683
Размерность ценового ряда достигает до 1,8
Ну и сам файл x_fractal_dim2.lua
1К |
Читайте на SMART-LAB:

NZD/CAD: цены испытывают давление под натиском продавцов?
Котировки кросс-курса NZD/CAD оттолкнулись от нисходящей трендовой линии, попутно сформировав свечную модель «медвежье поглощение». Судя по всему,...
22:12

Итоги 2025 года и прогнозы от аналитиков «Финама»: облигации
2025 год на рынке облигаций запомнился высокими процентными ставками, повышенной волатильностью и заметным смещением фокуса инвесторов в...
16:10
теги блога Маркин Павел
- Brent
- EUR USD
- Gold
- indicator
- LUA
- micex
- MOEX
- qlua
- quick
- quik
- ri
- rts
- S&P
- si
- treemapping
- usd
- акции
- алгоритм
- алготрейдинг
- аномалия
- АСВ
- банки
- Башнефть
- безграмотность
- биржа
- брокеры
- бюджет
- волатильность
- ВТБ
- Газпром
- голодовка
- дивиденды
- доллар
- звезда
- золото
- инвестор
- Индекс ММВБ
- Индикакаторы
- индикатор
- Инициативы ЦБ
- Карта рынка
- квик
- корреляция
- лидеры падения
- лидеры роста
- лидеры роста и падения ММВБ
- ликвидность
- ЛЧИ 2016
- Минфин
- ММВБ
- Набиуллина
- нетипичные объемы
- нефть
- НЛМК
- новость
- Облигации
- ограничения
- опек+
- опрос
- Опционы
- офз
- оффтоп
- приватизация
- Путин
- Распадская
- рейтинг
- риски
- робоадвайзинг
- роботы
- роснефть
- Россети
- Россия
- рост
- Ростелеком
- ртс
- рубль
- рынки
- рынок
- сарказм
- сбербанк
- Сечин
- смартлаб
- СОФТ
- срочный рынок
- статистика
- тарифы
- тарифы биржи
- тепловая карта
- технический анализ
- торговые сигналы
- трейдинг
- тренд
- Турция
- Улюкаев
- ФОРТС
- ФСК Россети
- ЦБ
- ЦБ России
- шорт
- юмор























с 29 сентября явный тренд, изменение индикатора в таких же пределах..
как то не показательно… может период более медленный выбрать?
К примеру вот человек долбил фрактальные размерности http://smart-lab.ru/blog/88632.php
а сейчас - https://mfd.ru/marketdata/barometer/
http://smart-lab.ru/blog/281180.php
ru.wikipedia.org/wiki/%D0%A0%D0%B0%D0%B7%D0%BC%D0%B5%D1%80%D0%BD%D0%BE%D1%81%D1%82%D1%8C_%D0%9C%D0%B8%D0%BD%D0%BA%D0%BE%D0%B2%D1%81%D0%BA%D0%BE%D0%B3%D0%BE