SMART-LAB
Новый дизайн
Мы делаем деньги на бирже
Блог им. over2u
Случайные закономерности. Закон арксинуса
- 14 октября 2015, 14:58
- |
Предыдущий пост собрал комментарии в большей части, посвященные распределению случайных величин. Многие называли арксинус и распределение, хотя пост был не о том. Но раз такой интерес к случайному распределению, то приведу свои мысли по этому поводу:
1. Случайное блуждание представляется многими как чередование положительных и отрицательных значений около некой средней линии (или линии тренда). Интуитивно кажется, что случайные величины должны находится примерно одинаковое количество в положительной и отрицательной зоне, достаточно равномерно чередуясь.
К сожалению интуиция нас подводит и в реальности случайное блуждание порождает волны (любителям Эллиота, Ганна и прочим привет), которые более вероятно будут находится либо выше, либо ниже средней линии большее количество времени. Собственно, первый закон арксинуса.
Практический вывод — торговать график эквити/баланса торговой стратегии с нулевым стат. преимуществом дело неперспективное (Привет торговцам портфелями стратегий).
2. Случайное блуждание делает не верифицируемыми торговые стратегии построенные на data mining. К этим стратам я бы также отнес любителей индикаторной торговли (вам тоже привет).
К примеру, вам показывают стейт с торговлей за 3 года (многие считают это более чем достаточно) на котором отражено 10 000 сделок (14 сделок в день, day trading), на протяжении 9 700 сделок счет находится в положительной зоне и лишь на протяжении 300 сделок в убыточной. Какова вероятность, что это просто удача? Интуиция подсказывает нам, что не более 1/1000 процента или около того и снова нас обманывает. В реальности 11.1%!
Вывод: вы должны знать свое стат. преимущество и на чем оно основано, иначе Вы блуждаете в случайных закономерностях и даете другим дурачить вас.
UPD: Спасибо за замечания, попровали wording (выделил жирным)
+ формула: 2/Pi*arcsin(A^0.5)
где A=K/N, K- положительный, N -всего
UPD 2: Пример случайного графика построенного в экселе на основании 1000 сделок (TP=SL)
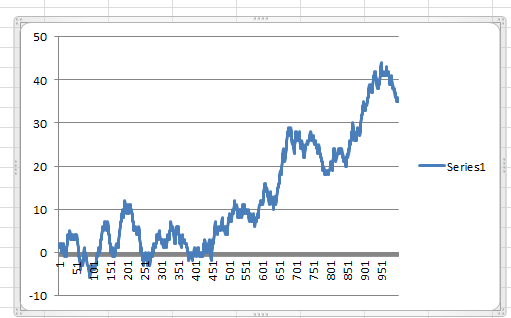
1. Случайное блуждание представляется многими как чередование положительных и отрицательных значений около некой средней линии (или линии тренда). Интуитивно кажется, что случайные величины должны находится примерно одинаковое количество в положительной и отрицательной зоне, достаточно равномерно чередуясь.
К сожалению интуиция нас подводит и в реальности случайное блуждание порождает волны (любителям Эллиота, Ганна и прочим привет), которые более вероятно будут находится либо выше, либо ниже средней линии большее количество времени. Собственно, первый закон арксинуса.
Практический вывод — торговать график эквити/баланса торговой стратегии с нулевым стат. преимуществом дело неперспективное (Привет торговцам портфелями стратегий).
2. Случайное блуждание делает не верифицируемыми торговые стратегии построенные на data mining. К этим стратам я бы также отнес любителей индикаторной торговли (вам тоже привет).
К примеру, вам показывают стейт с торговлей за 3 года (многие считают это более чем достаточно) на котором отражено 10 000 сделок (14 сделок в день, day trading), на протяжении 9 700 сделок счет находится в положительной зоне и лишь на протяжении 300 сделок в убыточной. Какова вероятность, что это просто удача? Интуиция подсказывает нам, что не более 1/1000 процента или около того и снова нас обманывает. В реальности 11.1%!
Вывод: вы должны знать свое стат. преимущество и на чем оно основано, иначе Вы блуждаете в случайных закономерностях и даете другим дурачить вас.
UPD: Спасибо за замечания, попровали wording (выделил жирным)
+ формула: 2/Pi*arcsin(A^0.5)
где A=K/N, K- положительный, N -всего
UPD 2: Пример случайного графика построенного в экселе на основании 1000 сделок (TP=SL)

989 |
Читайте на SMART-LAB:
⚡️ Комментируем сегодняшнюю новость об обращении за господдержкой
Друзья, привет! ⚡️ Комментируем сегодняшнюю новость об обращении за господдержкой. 💪 С конца 2024 года стратегия группы «Самолет» направлена на...
19:24

Итоги первичных размещений ВДО и некоторых розничных выпусков на 4 февраля 2026 г.
Следите за нашими новостями в удобном формате: Telegram , Youtube , RuTube, Smart-lab , ВКонтакте , Сайт
18:34
теги блога Vladimir K
- Bonds
- commodities
- COMMODITY TRAIDING
- Gold
- QIWI
- Ray Dalio
- S&P500
- TIPS
- vix
- акции
- Арбитраж
- аэрофлот
- башнефть
- вероятность
- волатильность
- Газпром
- Здравый смысл
- инвестиции
- Индексы
- макро
- мани менеджмент
- мани-менеджмент
- мемуары
- Путь становления трейдера
- рецензия на книгу
- риск
- риск менеджмент
- Роснефть
- Рэй Далио
- Скальпинг
- случайность
- специальные ситуации
- спред
- статистика
- стопы
- ТА
- теханализ
- технический анализ
- торговая стратегия
- торговля
- Торговые стратегии
- ТП
- трейдинг
- тройка диалог
- угадайка
- ФА
- фондовый рынок
- форекс
- ФСК Россети
- фундаментальный анализ
- холивар




















Найти стат. преимущество:) Например, вариант инвестирования на длительном сроке имеет стат. преимущество, связанное с ростом экономики.
Как ты высчитал, что 11,1% ??
2/Pi*arcsin(A^0.5)
где A=K/N, K- положительный, N -всего
Спрошу ахинею), но на полном серьёзе.
А как торговать, если соотношение прибыл./убыт. сделок. 43/57 не в мою сторону, а риск/профит 1к1.
Доп. есть множество дополнительных сложных параметров, которые я могу регулировать, в системе и они влияют на итоговую картину.
Собственно, есть ли какие либо способы теста, простые программки с возможность эмуляции различных вариаций, лучше в эксельке)) Да и речь не о торговли не на финансовом рынке. Заранее спасибо.
ключевое слово — биномиальное распределение.
упс, неправильно понял. не 9700 успехов, 300 неудач, а в течении длительного времени болтался выше нуля. тогда да, арксинус.
Вероятность описанного в примере события равна вероятности того, что стандартное нормальное распределение выкинет значение, превышающее по модулю 94:
Z = (0.97 — 0.5)/ Sqrt(0.5*(1-0.5)/10000) = 94. Я даже не могу представить, с какой точностью надо вычислять функцию распределения, чтобы найти первый ненулевой знак вероятности этого события. То есть, гипотеза о случайном везении отвергается при любом вообразимом уровне значимости.
Вот здесь написано, как проверяются такие гипотезы, стр 13-14:
www.hse.ru/data/2011/04/11/1210514602/%D0%BF%D0%BE%D1%81%D0%BE%D0%B1%D0%B8%D0%B5%20%D0%9F%D1%80%D0%BE%D0%B2%D0%B5%D1%80%D0%BA%D0%B0%20%D1%81%D1%82%D0%B0%D1%82.%20%D0%B3%D0%B8%D0%BF%D0%BE%D1%82%D0%B5%D0%B7,%20%D0%BC%D0%B0%D1%80%D1%82%202011.doc