Парный трейдинг с переключением режимов. Часть 1

По итогам последнего голосования на моем сайте победила статья Marco Bee  University of Trento — Department of Economics and Management,Giulio Gatti ,Università degli Studi di Trento — Department of Economics and Management — An Improved Pairs Trading Strategy Based on Switching Regime Volatility (Улучшенная стратегия парного трейдинга, основанная на переключении режимов волатильности). Ниже привожу перевод ее основных глав.

Введение

Стратегия, основанная на рыночно-нейтральном подходе, подразумевает, что трейдер должен принять три основные решения:

1. Выбрать активы для торговли из набора множества торгуемых инструментов
2. При существующем спреде ( т.е. динамически взвешенной разнице между двумя активами) определить его смысл в соответствующих эконометрических терминах
3. Выбрать торговый алгоритм

Если стратегия оперирует только одним активом, первая задача тривиальна, вторая исчезает и только третья остается действительно важной. В другом случае, при парном трейдинге, все задачи одинаково важны. 

Механизм статистического арбитража глубоко связан с концепцией баланса двух цен. Когда такой баланс нарушен, возникает возможность извлечения прибыли, при условии, что отношение баланса будет рано или поздно восстановлено. Такие модели страдают от трех видов рыночного поведения, которые могут быть описаны как:

1. Спред не сходится в дальнейшем: система никогда не будет прибыльной
2. Баланс восстанавливается медленно: некоторые стратегии могут закрыть позиции перед схождением спреда
3. Волатильность спреда возрастает: стратегия может перестать быть прибыльной, так как порог для сигнала входа в позицию преодолевается слишком рано и разница между двумя ценами расходится в ближайшем будущем.

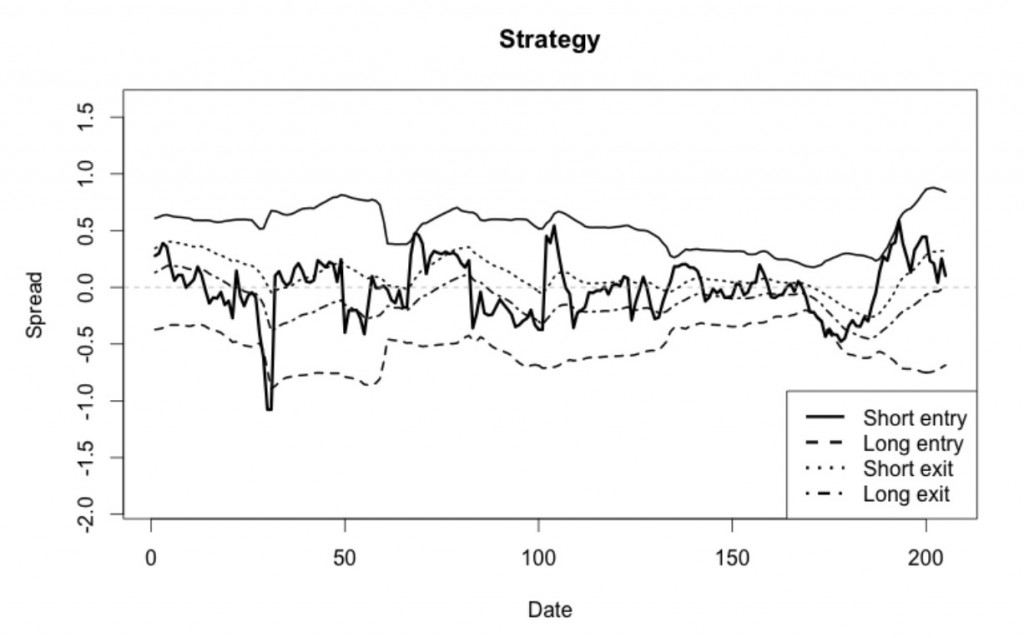
Цель модели, предлагаемой в данной статье — избежать негативных последствий, связанных с ростом волатильности, с попыткой получить дополнительную прибыль от него. Традиционные алгоритмы предписывают покупать (продавать) спред, когда цена выйдет за порог нижней (верхней) линии диапазона Боллинджера: мы предлагаем создать другие входные сигналы, согласованные с текущим режимом волатильности, найденные с помощью определения порогов, характеризующих данный режим. Мы исследуем два подхода к определению порогов: первый использует гауссовскую смесь двух распределений, второй использует марковскую модель скрытых состояний (НММ), для учета возможного присутствия некоторой временной зависимости.

Производительность этих подходов измерена на бэктестировании, результаты которого довольно хороши, так как стратегия показала большие доходность и коэффициент Шарпа, по отношению к обычным алгоритмам парного трейдинга.

Система тестировалась на 10 и 20 минутных ценах закрытия семи фьючерсных пар с октября 2012 года по сентябрь 2014 года. Две пары взяты из энергетического сектора — межрыночный спред между фьючерсом на нефть Лайт Свит (CL) и фьючерсом на нефть Брент (BRN), и сырьевая пара из мазута (HO) и бензина RBOB (RB). Из сельскохозяйственного сектора взяты пары фьючерсов на соевую муку (ZM) и соевое масло (ZL), а также на сою (ZS) и кукурузу (ZC). Последние три спреда созданы из мини фьючерсов на индекс Доу-Джонса (YM), Nasdaq (NQ) и S&P 500 (ES).

Обзор литературы

Выбор активов

Критерий минимального расстояния — это простой и интуитивно понятный метод, предложенный E. Gatev, W. N. Goetzmann, and K. G. Rouwenhorst. Pairs trading: Performance of a relative-value arbitrage rule. Review of Financial Studies, 19:797–827, 2006. Корреляционный фильтр позволяет нам найти порог и торговать парми, чья корреляция его превышает. Коинтеграционные фильтры (A. G. Modi, J. Desai, Dave A. R., and K. J. Desai. Finding the identical twin.Econometrics: Multiple Equation Models eJournal, 2011) были созданы в качестве альтернативы корреляции с целью нахождения долгосрочного взаимоотношения между двумя временными сериями. Значимость беты — другой простой инструмент, основанной на значимости коэфиициента регрессии бета между двумя временными сериями. Методы ETF, впервые предложенные M. Avellaneda and J. H. Lee. Statistical arbitrage in the US equities market. Quantitative Finance, 2010, выведены из хоошо известной концепции общих факторов риска. Здесь используются активы биржевых фондов — корзин активов с общими рыночными факторами, как инструменты хэджирования. В этой же статье также предлагается процедура, основанная на анализе принципиальных компонентов (метод машинного обучения) для выбора наилучших компонентов для целей торговли.

Моделирование спреда

Коэффициент минимальной дисперсии — это хорошо известная техника хэджирования ( например, J. C. Hull. Options, Futures, And Other Derivatives. Pearson, 8th edition, 2012), где коэффициент бета используется для взвешивания двух активов таким образом, что результирующая дисперсия портфеля минимизируется.

Обобщенный метод наименьших квадратов TLS (P. Teetor. Better hedge ratios for spread trading. Unpublished note, 2011. URL quanttrader.info/public/) использует тот факт, что для целей парного трейдинга, операции покупки одного актива и продажи другого или наоборот, не должны различаться. В случае классического метода наименьших квадратов (OLS) принимается во внимание дисперсия только одного актива из спреда — это приводит к ассиметричному учету рыночных факторов. С другой сторны, коэффициент хэджирования, найденный с помощью TLS согласован с рынком и дисперсия учитывается симметрично.

Другая возможность состоит в моделировании спреда как авторегрессивного процесса первого порядка. A. N. Burgess. A Computational Methodology for Modelling the Dynamics of Statistical Arbitrage. PhD thesis, London Business School, 1999 использует дискретный процесс, в то время, как W. K. Bertram. A non-stationary model for statistical arbitrage trading. SSRN,http://ssrn.com/abstract=1632718, 2010 применяет непрерывный подход.

Реже спред описывается моделью скрытых состояний Маркова. Первая версия была представлена в R. Bock and M. Mestel. A regime-switching relative value arbitrage rule. Operations Research Proceedings, 2008: согласно авторам, временной ряд спреда содержит структурные разрывы и предположение о постоянных параметрах становится неверным. Структурные разрывы в экономических и финансовых временных сериях возникают в результате финансовых кризисов, войн, политических изменений или пузырей в сырьевых активах, и могут влиять на параметры авторегрессии, коэффициенты регресии, средние значения, дисперсию или на параметры модели GARCH. Авторы статьи создают модель, где переключения режимов управляются марковскими цепями, текущий режим определяется ненаблюдаемой переменной и  основан на вероятности состояний. Формально, модель является процессом Маркова первого порядка с двумя состояниями, с переключающимися средним значением и дисперсией.

В статье A. Bucca and M. Cummins. Synthetic floating crude oil storage and optimal statistical arbitrage: A model specification analysis. SSRN, ssrn.com/abstract=1932432, 2011 вместо структурных разрывов анализируется коинтеграционные взаимоотношения между различными временными сериями. Описано, как коинтеграционная модель может иметь непостоянные параметры и может являться процессом с переключением среднего значения или трендовым процессом с переключением среднего, либо процессом с двумя режимами.

Иногда спред моделируется с использованием динамического процесса с латентной переменной, чьи параметры устанавливаются с помощью фильтра Калмана. Например, в E. P. Chan. Algorithmic Trading — Winning Strategies and Their Rationale. Wiley,2013 предлагается модель, которая рекурсивно вычисляет коэффициент регрессии, избегая дискретных решений или произвольного выбора.

В заключении, спред может быть описан в соответствии с физическими отношениями, исходящими из эмпирических свидетельств, основанных больше на экономических причинах. чем на математических моделях. Типичные примеры спредов на обвалах рынка рассмотрены в J. B. Mitchell. Soybean futures crush spread arbitrage: Trading strategies and market efficiency. Journal of Risk and Financial Management, 2010.

Выбор торгового алгоритма

Для торгового алгоритма простейшее решение — это гипотеза белого шума для спреда, которая предполагает, что спред является белым шумом. Некоторые применения оптимизируют коэффициент при дисперсии в диапазонах Боллинджера, другие (E. Gatev, W. N. Goetzmann, and K. G. Rouwenhorst. Pairs trading: Performance of a relative-value arbitrage rule. Review of Financial Studies, 19:797–827, 2006) устанавливают этот коэффициент равным 2, согласно 95% порговой величины нормального распределения.

Подобно приращениям, вычисленным из цен активов, в большинстве случаев эмпирические наблюдения говорят о том, что спред не следует нормальному распределению, соответственно, более сложный подход использует негауссовскую плотность распределения. Разные, возможно непараметрические, техники, могут быть созданы в порядке учета таких особенностей, например в G. Vidyamurthy. Pairs Trading — Quantitative Methods and Analysis. Wiley, 2004 используется альтернативный метод, основанный на смеси гауссовских распределений.

Моделирование скачков волатильности

Для определения, режим какой волатильности присутствует на рынке — высокой или низкой, могут быть применены различные инструменты. Общее допущение — спред является стационарным с ожидаемым значением, равным нулю. Для задачи моделирования всего распределения в данной статье мы используем два различных метода: первый, где спред определяется смесью двух гауссовских плотностей распределения; второй, где процесс генерации данных предполагается стохастическим процессом с переключением режимов волатильности. Последний метод является обобщением первого, где последовательность скрытых переменных генерирует набор зависимых наблюдений, следующих процессу Маркова, таким образом, возможные временные зависимости включены в модель. В следующих частях статьи, после определения понятия спреда, мы произведем глубокий анализ этих двух методов. При переходе к реальным данным, в обоих случаях гауссовской смеси и модели Маркова, мы будем, первое, определять два режима с идентичным ожидаемым средним значением, но разным стандартным отклонением, и, второе, плотность с более низкой дисперсией, ассоциируемой с бОльшим параметром вероятности.

Модель гауссовской смеси

Плотность распределения смеси двух наборов нормальных плотностей определяется следующим образом:

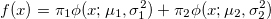
где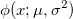 — нормальная плотность распределения с параметрами μ,σ2 и 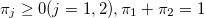, так что мы можем принять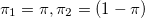. Тогда мы можем переписать формулу следующим образом:

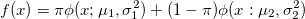
Вектор неизвестных параметров определим как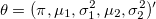, содержащий вероятность принадлежности к первому распределению 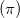, и ожидаемое значение и дисперсию обоих распределений вероятности.

Модель Маркова

Вторая модель была предложена для целей парного трейдинга в статье R. Bock and M. Mestel. A regime-switching relative value arbitrage rule. Operations Research Proceedings, 2008. Но марковские модели использовались и намного раньше. Для их вычисления был создан алгоритм максимального правдоподобия на основе EM алгоритма, предложенный J. D. Hamilton. Analysis of time series subject to changes in regime. Journal of Econometrics, 45:39–70, 1990 .  В предложенной модели режимы переключаются в зависимости  от последовательностей Маркова. Режим определяется скрытыми переменными, и вывод о текущем режиме основан на вероятности состояний. Используемый здесь процесс имеет два режима, с переключающимися значениями средней и дисперсии. Хотя, в принципе, может быть неразумно иметь дело только с фиксированными средними значениями, данная модель с переключением производит лучшие оценки.

Основная разница между  нашей моделью и моделью Bock и Mestel (2008) лежит в плоскости предмета моделирования. В то время, как у них определяемым значением является коэффициент хэджирования, наша временная серия — это сам спред, а не его компоненты. Формально, процесс определяется как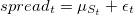, где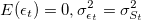

Отметим. что в определении модели Bock и Mestel переключения среднего значения были необходимостью. В нашем случае, при использовании модели для спреда, являющегося стационарным процессом, такой необходимости нет.

В следующей части мы определим устойчивую модель парного трейдинга для различных режимов волатильности и протестируем ее на реальных данных.

Продолжение и другие стратегии алгоритмической торговли смотрите на моем сайте — www.quantalgos.ru