NASDAQ опубликовал пресс-релиз* со списком 6 компаний, которые будут включены в NASDAQ100 21 декабря (и, соответственно, 6 выбывающих).

Однако не опубликовал (и даже не дал ссылки на) ни формулы расчета индекса (после 21 декабря), ни хотя бы весовых коэффициентов, которые будут работать в этой формуле… Это нормально вообще?

Кто-нибудь знает место, где эту формулу (веса, конечно, сама-то формула понятна: взвешенная сумма текущих котировок) можно увидеть?
_________________________
* см. www.nasdaq.com/press-release/annual-changes-to-the-nasdaq-100-index-2020-12-11

Есть две акции — Q и U, изменение цены которых во времени — Q(t) и U(t).

Торгуется синтетическая бумага Z, состоящая из Q и U, такая что:

1) все средства торгового счёта постоянно в этой синтетической бумаге;

2) постоянно поддерживается соотношение — 90% средств в бумаге Q и 10% — в бумаге U.

Какой формулой описывается изменение во времени цены бумаги Z?

В Википедии https://en.wikipedia.org/wiki/NASDAQ-100 приведён список из 103 бумаг (от ровно 100 эмитентов) в составе Nasdaq 100 по состоянию на «October 19, 2020»… а в этой таблице https://www.nasdaq.com/market-activity/quotes/nasdaq-ndx-index всего 98 строчек… что к чему — не пойму.

Существуют ли ETF, отслеживающие NASDAQ Financial 100? Если да, то не подскажите названия?

Разберём сначала — для введения терминологии — длинную сделку.

Трейдер купил акции на сумму С по цене Ц1, а потом продал по цене Ц2 — сколько трейдер заработал, и сколько у него стало денег?
На каждой акции он заработал Ц2-Ц1, а всего он держал число акций С/Ц1, значит заработал он 

С/Ц1*(Ц2-Ц1) = С*(Ц2/Ц1-1), и теперь у него стало денег 

С*(Ц2/Ц1-1) + С = С*Ц2/Ц1 — всё логично.

Теперь трейдер продаёт в короткую акции на сумму С по цене Ц1, а потом откупает по цене Ц2. На каждой акции он «сэкономил» Ц1-Ц2, а всего он «задействовал» акций С/Ц1, значит заработал он

С/Ц1*(Ц1-Ц2) = С*(1-Ц2/Ц1), и теперь у него стало денег 

С*(1-Ц2/Ц1) + С = 2С — С*Ц2/Ц1 — так брокер рассчитывается с трейдером по короткой сделке?

Предположим, некто дал мне в управление пакет акций AAPL. И у меня такой странный бзик — я очень верю в долгосрочный рост ровно двух акций: этого AAPL и MSFT. Поэтому я решил, что буду всегда в этих акция — либо в одной, либо в другой. То есть продав одну, я сразу буду покупать другую на всю вырученную сумму.

Но как мне настроить свою торговую систему для такой торговли? Да запросто: я построю «ценовой ряд» MSFT/AAPL (поделю по-барно историческую цену MSFT на цену AAPL) и настрою свою торговую систему на этот ряд. Покупка этого ряда будет означать, что вся моя «buying power» вложена в MSFT, а выход из этого «инструмента» будет означать, что я вернулся в AAPL. И в конце, когда мой контракт на управление пакетом акций AAPL закончится, я именно закрою позицию по этому своему инструменту MSFT/AAPL (если она будет) и рассчитаюсь со своим доверителем получившимися акциями AAPL, поделив навар (также выраженный в AAPL) согласно оговоренным условиям.

Видно, что в рамках этой парадигмы возможны только длинные позиции по инструменту MSFT/AAPL… Однако по жизни мой брокер позволяет мне торговать и в короткую. И, например, моя система торговли тоже включает в себя короткие позиции. И, возможно, ряд MSFT/AAPL даёт очень хорошие короткие позиции для этой моей системы...

Вопрос: как в рамках этой парадигмы реализовать короткую позицию? Что я должен предпринять с MSFT и, отдельно, с AAPL, чтобы получить эквивалент короткой позиции по MSFT/AAPL?

Запишу формулу ЕМА в двух слегка необычных видах: сначала

ЕМА = ЕМА(-1) + beta * (X - ЕМА(-1)) — а потом ещё (просто для фана, на самом деле):

ЕМА — ЕМА(-1) = beta * (X - ЕМА(-1))
(эту вторую формулу просто приятно интерпретировать: «движение» ЕМА составляет «бетову часть» от смещения Х относительно ЕМА(-1) ).

Эти формулы имеют одно примечательное философическое свойство: (следующее) значение ЕМА не зависит от (предыдущего/предыдущих) значения Х.

С одной стороны, это утверждение очевидно до банальности — не входит в формулу X(-1), и точка. С другой стороны, понятно, что Х(-1) (и все предыдущие «иксы») повлияло (на предыдущем шаге/предыдущих шагах) на значение ЕМА(-1), то есть Х(-1) как бы «свёрнуто» в ЕМА(-1).

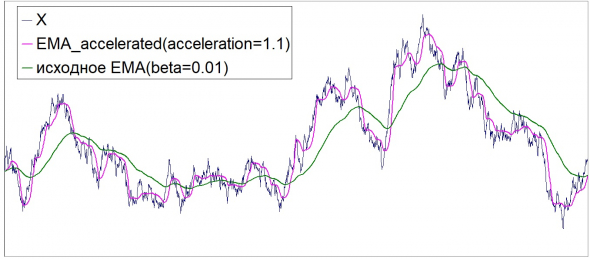
Но факт остаётся фактом: непосредственно (явным образом) — не зависит. То есть, например, представим себе два разных ряда Х и на обоих построены ЕМА с beta = 0.01. И пусть у обоих рядов в некотором месте ЕМА(-1) = 100, а Х = 90. В обоих случаях ЕМА будет равно 99.9 .

То есть, например, у первого ряда Х(-1) было равно 101, и движение к Х=90 (т.е. «вниз на 11») порождает ЕМА=99.9 ...
А у второго ряда Х(-1) было равно 1010 (то есть в 10 раз больше, чем у первого), но движение к  Х=90 («вниз на 920») порождает то же самое ЕМА=99.9 . По-моему, это весьма забавно.

ЕМА, ЕМА(ЕМА), ЕМА(ЕМА(ЕМА))), ...

К какому ЕМА  — к ЕМА с каким beta* — ближе всего линия повторного ЕМА:

DEMA(beta1, beta2; t) = ЕМА(beta1; ЕМА(beta2; t))

?
__________________
* в нотации: ЕМА(beta; t) = (1-beta) * ЕМА(beta; t-1) + beta* X(t)