SMART-LAB
Новый дизайн
Мы делаем деньги на бирже
Ivan FXS
Задачка по скринингу
- 28 января 2023, 20:35
- |
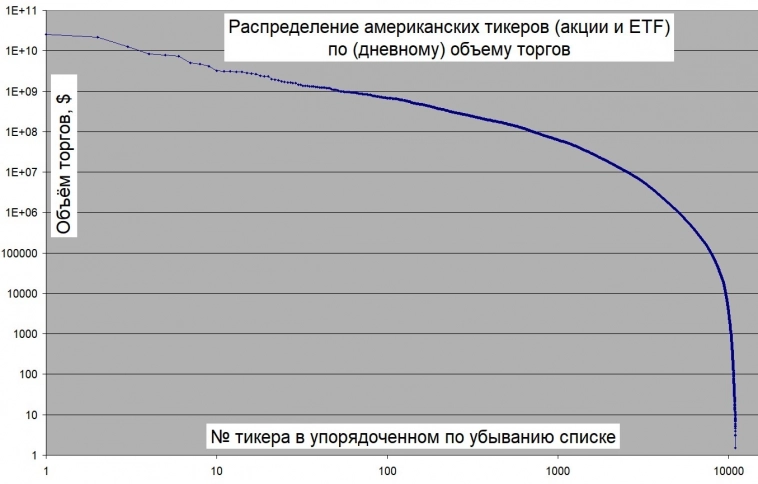
Вам дали 10000 числовых рядов формата (календарная дата; число) и предложили рассортировать их пополам на «похожие на (цены) американские акции» и непохожие. Или, скажем, «более похожие» и «менее похожие». Как вы будете это делать?
- комментировать
- 228
- Комментарии ( 6 )
Ликбез по названиям американских компаний: Acquisition
- 27 января 2023, 01:11
- |
Почему в названиях американских компаний, торгуемых на биржах, так часто используется слово «Acquisition», несет ли оно какую-то специфическую смысловую нагрузку? Само по себе оно звучит банально: ну, «приобретение», кто-то приобрел, раз владеет, не может быть компании, которая никем не приобретена… зачем, казалось бы, впихивать в название такое длинное банальное слово?
Ликбез по аукционам (на закрытии/открытии сессии)
- 24 января 2023, 23:57
- |
Предположим, сейчас цена=100, и я ставлю лимитный ордер на продажу по 110. И вплоть до самого аукциона (на закрытии сессии, например) цена не доходит до 110, а на аукционе цена оказывается =115.
1) возможно такое?
2) по какой цене будет исполнен мой ордер?
1) возможно такое?
2) по какой цене будет исполнен мой ордер?
Ликбез по опционам: зависимость от срока до экспирации
- 24 ноября 2022, 22:36
- |
У меня на реальных данных получается, что цена опционов At_the_money зависит от времени до экспирации почти как корень квадратный (показатель степени 0.53). Это нормально?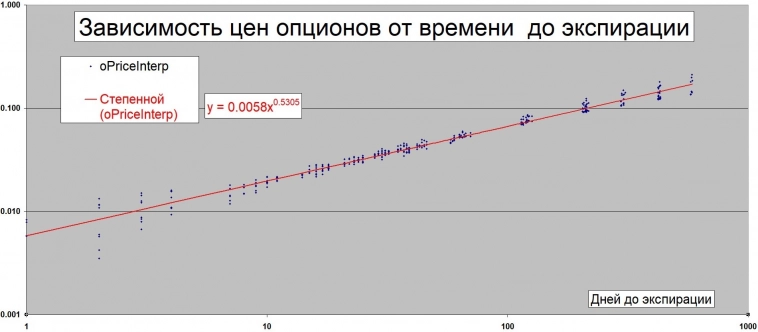

Ликбез (задачка) по опционам
- 20 ноября 2022, 23:26
- |
Предположим на некоторой бирже торгуются одновременно (параллельно) и европейские, и американские опционы.
Как будут различаться их цены — какие будут дороже и насколько (последнее — в зависимости от времени до экспирации наверное очевидно)?
Как будут различаться их цены — какие будут дороже и насколько (последнее — в зависимости от времени до экспирации наверное очевидно)?
Может быть, это не правильные пчелы и они делают неправильный мед?
- 20 ноября 2022, 02:13
- |
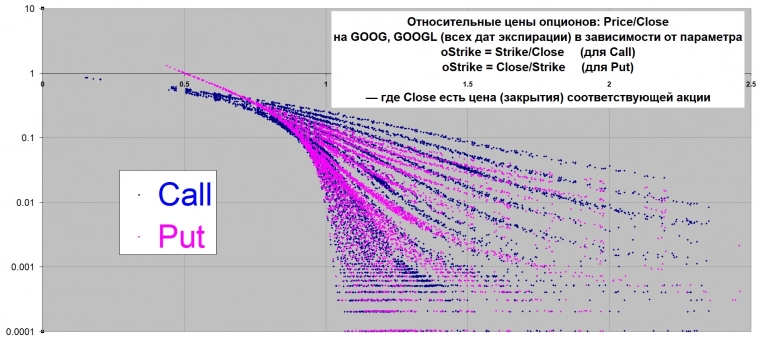
на всякий случай — легенда в текстовом виде:
Относительные цены опционов: Price/Close
на GOOG, GOOGL (всех дат экспирации) в зависимости от параметра
oStrike = Strike/Close (для Call)
oStrike = Close/Strike (для Put)
— где Close есть цена (закрытия) соответствующей акции
Задачка: белых в два раза больше, чем чёрных
- 03 июня 2021, 11:00
- |
Задачка
Про акцию А известно, что в её графике цены белых баров примерно в два раза больше, чем чёрных.
Дает ли это знание возможность зарабатывать на торговле этой акцией?
Про акцию А известно, что в её графике цены белых баров примерно в два раза больше, чем чёрных.
Дает ли это знание возможность зарабатывать на торговле этой акцией?
Общее изложение построения "усредняемой" торговой системы по методу Монте-Карло
- 27 апреля 2021, 11:38
- |
0. Дано: имеем модель торговой системы с некоторым набором свободных параметров, которая допускает «усреднение по параметрам», то есть для любой пары наборов Р1 и Р2 можно вычислить средне — (Р1+Р2)/2 — и это будет тоже набор параметров, с которым может запускаться используемая нами модель торговой системы.
1. Разбиваем исторические данные на три участка: оптимизационный, контрольный и супер-контрольный.
2. Генерируем огромное количество случайных наборов параметров Рi (отсюда «Монте-Карло») и для каждого вычисляем качество Qi работы системы на оптимизационном участке данных и, отдельно, QQi — на контрольном участке. Все результаты записываем.
3. Упорядочиваем Qi по убыванию — в ряд Qj (т.е. j — индекс в порядке убывания Q), и начинаем идти по этому списку, усредняя, Рj, Qj и QQj — в Рk, Qk и QQk:
Рk = Среднее(Рj)
Qk = Среднее(Qj)
QQk = Среднее(QQj) — все усреднения — по j=1..k
4. Понятно, что Qk будет монотонно убывать (хорошо, хорошо, не убывать, а «не возрастать»), а Рk и QQk будут сначала скакать, а потом стабилизируются. Смотрим на поведение QQk и надеемся увидеть — после стабилизации — некоторый (локальный) максимум (при k равном некоторому m), после которого начнётся монотонное снижение. Также надеемся, что будет QQm ~ Qm.
5. Если всё так, то Pm — тот набор параметров, который нужно проверить на супер-конрольном участке данных и… да будет нам счастье!
1. Разбиваем исторические данные на три участка: оптимизационный, контрольный и супер-контрольный.
2. Генерируем огромное количество случайных наборов параметров Рi (отсюда «Монте-Карло») и для каждого вычисляем качество Qi работы системы на оптимизационном участке данных и, отдельно, QQi — на контрольном участке. Все результаты записываем.
3. Упорядочиваем Qi по убыванию — в ряд Qj (т.е. j — индекс в порядке убывания Q), и начинаем идти по этому списку, усредняя, Рj, Qj и QQj — в Рk, Qk и QQk:
Рk = Среднее(Рj)
Qk = Среднее(Qj)
QQk = Среднее(QQj) — все усреднения — по j=1..k
4. Понятно, что Qk будет монотонно убывать (хорошо, хорошо, не убывать, а «не возрастать»), а Рk и QQk будут сначала скакать, а потом стабилизируются. Смотрим на поведение QQk и надеемся увидеть — после стабилизации — некоторый (локальный) максимум (при k равном некоторому m), после которого начнётся монотонное снижение. Также надеемся, что будет QQm ~ Qm.
5. Если всё так, то Pm — тот набор параметров, который нужно проверить на супер-конрольном участке данных и… да будет нам счастье!
Солдат спит, а QQQ растёт
- 22 февраля 2021, 16:26
- |
C 13.08.2009 (условно говоря, после выхода из кризиса 2008 года) по 30.11.2020 QQQ (это ETF, отслеживающий индекс NASDAQ100) вырос с 35.908 до 299.62 (то есть в 8.3 раза).
«В логарифмической терминологии»: Ln(QQQ) вырос на 2.12.
Из этих 2.12 только 0.63 — меньше трети, примерно 2/7 — приходится на «движения во время торговых сессий»{то есть Сумма(Ln(Close)-Ln(Open)) }
— остальные 5/7 (накопленного) роста — это рост между (вне) торговыми сессиями.
«В логарифмической терминологии»: Ln(QQQ) вырос на 2.12.
Из этих 2.12 только 0.63 — меньше трети, примерно 2/7 — приходится на «движения во время торговых сессий»{то есть Сумма(Ln(Close)-Ln(Open)) }
— остальные 5/7 (накопленного) роста — это рост между (вне) торговыми сессиями.
теги блога Ivan FXS
- DJIA
- DMA
- EMA
- ETF
- GOOG
- GOOGL
- mlp
- NASDAQ
- Nasdaq 100
- nasdaq100
- NYSE
- OHLC
- QQQ
- S&P500
- S&P500 фьючерс
- SP100
- Trailing Stop
- акции
- акции США
- алгоритмическая торговля
- альфа-директ
- аукцион
- аукцион закрытия
- брокеры
- вопрос
- генетические алгоритмы
- гистограмма
- данные
- ЕМА
- Задачка
- инвестиции
- индексы
- индексы акций
- индикатор
- история акций
- короткие продажи
- маркетмейкеры
- мнк
- модели
- моделирование
- монте-карло
- мтс
- нейронные сети
- оптимизация
- опцион
- опционы
- ордер
- парадокс
- прогноз
- регрессия
- сигнал
- случайное блуждание
- спреды
- стоп
- тикеры
- торговые роботы
- трейдинг
- финансовая математика