SMART-LAB
Новый дизайн
Мы делаем деньги на бирже
Блог им. ognevoy
ТЕОРИЯ ВЕРОЯТНОСТЕЙ
- 08 апреля 2012, 22:46
- |
ВЕРОЯТНОСТЕЙ ТЕОРИЯ
занимается изучением событий, наступление которых достоверно неизвестно. Она позволяет судить о разумности ожидания наступления одних событий по сравнению с другими, хотя приписывание численных значений вероятностям событий часто бывает излишним или невозможным. [...]
ЭЛЕМЕНТАРНАЯ ТЕОРИЯ
В очень простых ситуациях интуитивно ясно, каким образом можно приписать вероятности отдельным событиям. Например, если в коробку положить 8 красных и 2 белых фишки для игры в покер и хорошенько потрясти ее, то представляется более вероятным, что, извлеченная из коробки, наудачу, фишка окажется красной; и действительно, вероятность извлечь красную фишку в четыре раза больше вероятности извлечь белую фишку. Так как это испытание (извлечение из коробки первой фишки) имеет 10 возможных исходов, из которых 8 приходится на долю красных фишек, то доля благоприятных исходов подсказывает, что вероятность извлечь красную фишку составляет 8/10 или 4/5. Ту же самую ситуацию нередко формулируют иначе, говоря, что шансы вынуть красную фишку равны 4 к 1; шансы p к q означают, что какое-то событие происходит с вероятностью p/(p + q).
Аналогично при бросании симметричной игральной кости выпадению любой грани естественно приписать вероятность 1/6, а если мы бросаем симметричную монету, то любой из исходов — выпадение «орла» или «решки» — имеет вероятность 1/2. Но стоит перейти к более сложным событиям, как помощь со стороны интуиции становится менее надежной.
Предположим, что мы бросаем две симметричные монеты. Существуют три возможных исхода: два «орла», две «решки» или «орел» и «решка». Большинство людей, поразмыслив, согласятся с тем, что этим исходам нельзя приписывать одну и ту же вероятность, поскольку два «орла» могут выпасть только в том случае, если первая монета выпадет вверх «орлом» и вторая монета также выпадет вверх «орлом», в то время как комбинация «орел» и «решка» возможна и если первая монета выпадет вверх «орлом», а вторая — вверх «решкой», и если первая монета выпадет вверх «решкой», а вторая — вверх «орлом». Короче говоря, анализ показывает, что трем возможным исходам бросаний двух монет следует приписать вероятности 1/4, 1/4 и 1/2. Корректность такого подхода можно подтвердить бросанием реальных монет в той же степени, в какой физические эксперименты подтверждают большинство законов природы. В более сложных ситуациях интуиция окончательно отказывает, и для того, чтобы правильно приписать ту или иную вероятность сложному событию, требуется некий математический инструмент ее подсчета. Вычисление вероятностей тесно связано с комбинаторным анализом, посвященным подсчету числа способов, которыми можно разместить те или иные объекты, или количества тех или иных событий, которые могут произойти при различных условиях. Элементарные вероятности определяются отношением числа случаев, при которых происходит интересующее нас событие (благоприятный исход), к общему числу случаев. Например, две игральные кости могут выпасть 36 способами, из которых только в 6 случаях сумма выпавших очков равна 7, поэтому вероятность выпадения 7 очков на двух костях равна 1/6. Два события, которые не могут происходить одновременно, называются взаимоисключающими. Например, при однократном бросании игральной кости 5 очков и 6 очков одновременно выпасть не могут. Вероятность того, что произойдет одно или другое взаимоисключающее событие, равна сумме вероятностей этих событий. Например, вероятность того, что при однократном бросании кости выпадет либо 5, либо 6 очков, равна 1/6 + 1/6 = 1/3.
Вероятность достоверного события (которое заведомо наступит) принимается равной 1, а вероятность события, наступление которого невозможно, считается равной 0. Очевидно, что наступление и ненаступление данного события взаимно исключают друг друга, а потому, если вероятность наступления какого-нибудь события равна p, то вероятность его ненаступления будет 1 — p. Однако в более сложных задачах, когда число возможных исходов бесконечно велико, вероятность нельзя задать с помощью простого перечисления всех возможных случаев. Например, если мы представим себе испытание, состоящее в бесконечной серии бросаний симметричной монеты, то ситуация, когда во всех бросаниях выпадают только «орлы», в принципе не невозможна, хотя такому исходу необходимо приписать вероятность, равную 0, так как в высшей степени «невероятно», чтобы в любой достаточно длинной серии бросаний выпадали только «орлы». Для детального анализа вероятностных задач, более сложных, чем простые азартные игры, необходима более строгая и абстрактная формулировка. Именно она и будет рассмотрена ниже.
Основной принцип комбинаторного анализа гласит: если что-либо одно можно осуществить m способами, а нечто другое — n способами, то эти действия последовательно можно осуществить mґn способами. [...]Например, Четверых людей можно выстроить в ряд 4*3*2*1 = 24 способами, так как первого можно выбрать 4 способами, второго — 3 способами, третьего — 2 способами, а четвертого — только одним. Но четырех людей можно посадить в четыре автобуса 4*4*4*4 = 256 способами, так как каждый из них может сесть в любой из четырех автобусов.
Перестановки и сочетания. Многие задачи теории вероятностей удается проанализировать, если воспользоваться некоторыми следствиями из приведенного выше комбинаторного принципа. Размещение предметов в определенном порядке называется перестановкой этих предметов. Например, существуют шесть перестановок чисел 1, 2, 3, а именно: 1, 2, 3; 1, 3, 2; 2, 1, 3; 2, 3, 1; 3, 1, 2; 3, 2, 1. Число перестановок из n предметов равно 1*2*3*… *n. Сокращенно это число записывается как n! (и читается как «факториал числа n» или «n факториал»). Любое размещение предметов, порядок которых не имеет значения, называется сочетанием. Из набора чисел 1, 2, 3, 4, 5 можно извлечь десятью различными способами любые два числа, если мы условимся не различать пары, состоящие из одних и тех же чисел, взятых в различном порядке, т.е., например, не различать 1, 2 и 2, 1. Если из двенадцати человек нужно выбрать комитет в составе девяти членов, то это можно сделать столькими способами, сколько сочетаний из двенадцати по девять мы можем составить. Это, естественно, относится к случаю, когда сам порядок размещения членов внутри комитета несуществен. Однако число разных баскетбольных команд, которые можно составить из тех же двенадцати человек, равно числу перестановок из девяти элементов, которые можно набрать из этих двенадцати, так как в баскетбольной команде каждый игрок имеет свой номер. Вторая задача для анализа проще: существуют 12*11*10*9*8*7*6*5*4 перестановок, так как первый номер можно выбрать 12 различными способами, второй номер — 11 способами и т.д., пока мы не дойдем до последнего, девятого, номера, который может быть выбран четырьмя способами. В первой задаче любая из 9! перестановок девяти членов комитета приводит к одному и тому же составу комитета, так как состав комитета не зависит от того, в каком порядке перечислять его членов; иначе говоря, число перестановок 12*11*10*9*8*7*6*5*4 дает ответ, который в 9! раз больше, чем нужно. Следовательно, число сочетаний из двенадцати человек по девять равно указанному произведению, деленному на 9!, или
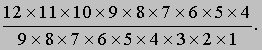
=220. В общем случае число сочетаний из n по r равно n (n — 1)(n — 2)… (n — r + 1)/r! или n!/r!(n — r)! Это число называется биномиальным коэффициентом
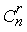
Еще один полезный принцип состоит в утверждении, что n предметов можно разложить в r коробок rn различными способами, если в любой коробке может находиться любое число предметов.
Обратимся теперь к некоторым приложениям этих принципов. 1) Какова вероятность выпадения ровно двух шестерок при пяти бросаниях игральной кости (или, что то же, при одном бросании пяти костей)? Пять костей могут выпасть 65 способами. Две кости, на которых выпали шестерки, можно выбрать способами (сочетания появляются потому, что порядок, в котором выпадают шестерки, несуществен), т.е. (5*4*3*2*1)/((2*1) * (3*2*1)) = 10 способами. Нешестерки (их 5: 1, 2, 3, 4 и 5 очков) на остальных 3 костях могут выпасть 53 способами. Следовательно, мы получаем ровно две шестерки из пяти бросаний 10*53 способами; искомая вероятность, таким образом, равна 10*53/65 или 1250/7776, т.е. ок. 1/6.
2) Какова вероятность получить ровно два туза, если из колоды, состоящей из 52, извлекаются 5 карт? Извлечь из колоды 5 карт можно способами. Пять карт, из которых два туза, а остальные три — нетузы, можно получить, извлекая два туза способами, а три нетуза — способами. Искомая вероятность равна
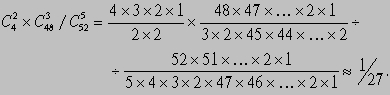
СОВРЕМЕННАЯ ТЕОРИЯ ВЕРОЯТНОСТЕЙ
Современная теория вероятностей, подобно другим разделам математики, например геометрии, состоит из результатов, выводимых логическим путем из некоторых основных утверждений, или аксиом, и приложений к ситуациям в реальной жизни, относительно которых предполагается, что они согласуются с аксиомами. Трудность теории вероятностей заключается в том, что объекты, составляющие предмет ее изучения, носят гораздо более общий характер и поэтому не столь наглядны, как, например, объекты геометрии или механики. Теория вероятностей занимается изучением событий и их вероятностей, представляемых числами, заключенными в интервале от 0 до 1. В случае исторически знаменитых задач, связанных с азартными играми, можно интуитивно понять, как должна быть сформулирована соответствующая математическая задача. Такая задача обычно имела следующий вид: заданы вероятности некоторых элементарных событий; требуется вычислить вероятность какого-нибудь более сложного события, связанного с элементарными событиями некоторым простым образом. Прежде чем мы более подробно представим современную теорию, полезно проиллюстрировать интуитивную теорию и ее методы на примере. Вычислим вероятность того, что некоторому игроку в бридж достанется один или несколько тузов. В качестве элементарных событий удобно рассматривать получение на руки возможных вариантов из 13 карт. Необходимо, чтобы распределение вероятностей между наборами имеющихся у игроков карт, т.е. элементарными событиями, отражало наше убеждение в том, что карты сдавались весьма специальным образом, а именно случайно. Постулат, который мы примем, сводится к определению того, что мы понимаем под случайной сдачей карт. Мы постулируем, что любой набор из 13 карт, который может достаться игроку при раздаче, равновероятен. Какова эта вероятность? Ответ на этот вопрос может дать интуитивно очевидный принцип, служащий основным методом теории вероятностей: если имеется несколько взаимоисключающих событий (таких, что каждый раз происходит только одно из них), то вероятность того, что произойдет по крайней мере одно из них, равна сумме вероятностей каждого из событий в отдельности.
Кроме того, потребуем, чтобы вероятность события, которое заведомо происходит, была равна единице. Сделанные замечания позволяют решить нашу задачу. Пусть n — число различных вариантов наборов карт, которые может получить игрок, A1, A2, ..., An — события, соответствующие получению каждого из этих наборов, и P(A1), P(A2), ..., P(An) — вероятности этих событий. Пусть A — событие, состоящее в том, что игрок получает набор карт, содержащий один или несколько тузов, и m — число наборов из 13 карт, каждый из которых содержит один или несколько тузов, B1, B2, ..., Bm — события, соответствующие получению такого набора. Тогда A — событие, состоящее в том, что наступает одно из множества событий B1, B2, ..., Bm. Наконец, пусть P (A) — вероятность события A. Так как события A1, A2, ..., An равновероятные и взаимоисключающие, причем одно из них достоверно происходит, то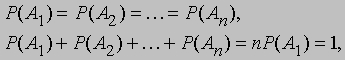
и, следовательно,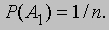
Аналогично,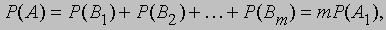
в силу чего окончательно получаем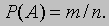
Этот результат сводит исходную задачу к чисто комбинаторной задаче нахождения чисел m и n. Последняя легко решается с помощью теории перестановок и сочетаний, некогда бывшей существенной частью теории вероятностей, но ныне таковой не являющейся. Число n есть просто число способов, которыми можно выбрать 13 карт из 52. Используя стандартные обозначения, находим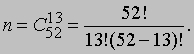
Вместо числа m проще найти число (n — m) — число наборов из 13 карт, не содержащих ни одного туза, или число способов, которыми можно выбрать 13 карт из 48: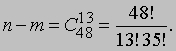
Следовательно,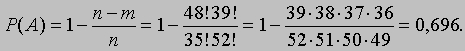
Было бы ошибкой полагать, что решение любой вероятностной задачи всегда можно представить в виде простого отношения двух чисел вида P (A) = m/n. Приведенное рассуждение показывает, что такое отношение (числа благоприятных случаев к общему числу случаев) выражает вероятность, которую требуется найти, если элементарные события равновероятны.
По-видимому, наиболее важной ситуацией, в которой изложенный выше метод неприменим, является биномиальное распределение вероятностей. Представим себе, что некоторое испытание проводится n раз, причем каждый раз его исход может быть либо благоприятным У («успех»), либо неблагоприятным Н («неудача»). Элементарными событиями можно считать все возможные последовательности У и Н (их общее число равно 2n), каждая такая последовательность содержит n символов. В этом случае вероятности элементарных событий невозможно вывести из постулата о равновероятности всех последовательностей из n символов, содержащих одинаковое количество У и Н. Их невозможно получить и из дополнительного постулата о том, что вероятность отдельного благоприятного исхода равна p, а вероятность одного неблагоприятного исхода равна 1 — p. Необходимо также в явном виде указать, каким образом вероятность будущих исходов испытаний зависит от прошлых исходов.
Простейшее предположение состоит в том, что будущие исходы не зависят от прошлых, что довольно часто встречается на практике.
Его можно формально выразить, постулировав, что вероятность любой заданной последовательности У и Н равна произведению вероятностей отдельных исходов. При таких предположениях вероятность, например, последовательности исходов УУУНУНН равна p4(1 — p)3. Нетрудно показать, что в общем случае вероятность получения ровно k благоприятных исходов в n испытаниях равна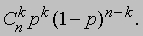
Вся статья http://dic.academic.ru/dic.nsf/enc_colier/6347/ВЕРОЯТНОСТЕЙ
занимается изучением событий, наступление которых достоверно неизвестно. Она позволяет судить о разумности ожидания наступления одних событий по сравнению с другими, хотя приписывание численных значений вероятностям событий часто бывает излишним или невозможным. [...]
ЭЛЕМЕНТАРНАЯ ТЕОРИЯ
В очень простых ситуациях интуитивно ясно, каким образом можно приписать вероятности отдельным событиям. Например, если в коробку положить 8 красных и 2 белых фишки для игры в покер и хорошенько потрясти ее, то представляется более вероятным, что, извлеченная из коробки, наудачу, фишка окажется красной; и действительно, вероятность извлечь красную фишку в четыре раза больше вероятности извлечь белую фишку. Так как это испытание (извлечение из коробки первой фишки) имеет 10 возможных исходов, из которых 8 приходится на долю красных фишек, то доля благоприятных исходов подсказывает, что вероятность извлечь красную фишку составляет 8/10 или 4/5. Ту же самую ситуацию нередко формулируют иначе, говоря, что шансы вынуть красную фишку равны 4 к 1; шансы p к q означают, что какое-то событие происходит с вероятностью p/(p + q).
Аналогично при бросании симметричной игральной кости выпадению любой грани естественно приписать вероятность 1/6, а если мы бросаем симметричную монету, то любой из исходов — выпадение «орла» или «решки» — имеет вероятность 1/2. Но стоит перейти к более сложным событиям, как помощь со стороны интуиции становится менее надежной.
Предположим, что мы бросаем две симметричные монеты. Существуют три возможных исхода: два «орла», две «решки» или «орел» и «решка». Большинство людей, поразмыслив, согласятся с тем, что этим исходам нельзя приписывать одну и ту же вероятность, поскольку два «орла» могут выпасть только в том случае, если первая монета выпадет вверх «орлом» и вторая монета также выпадет вверх «орлом», в то время как комбинация «орел» и «решка» возможна и если первая монета выпадет вверх «орлом», а вторая — вверх «решкой», и если первая монета выпадет вверх «решкой», а вторая — вверх «орлом». Короче говоря, анализ показывает, что трем возможным исходам бросаний двух монет следует приписать вероятности 1/4, 1/4 и 1/2. Корректность такого подхода можно подтвердить бросанием реальных монет в той же степени, в какой физические эксперименты подтверждают большинство законов природы. В более сложных ситуациях интуиция окончательно отказывает, и для того, чтобы правильно приписать ту или иную вероятность сложному событию, требуется некий математический инструмент ее подсчета. Вычисление вероятностей тесно связано с комбинаторным анализом, посвященным подсчету числа способов, которыми можно разместить те или иные объекты, или количества тех или иных событий, которые могут произойти при различных условиях. Элементарные вероятности определяются отношением числа случаев, при которых происходит интересующее нас событие (благоприятный исход), к общему числу случаев. Например, две игральные кости могут выпасть 36 способами, из которых только в 6 случаях сумма выпавших очков равна 7, поэтому вероятность выпадения 7 очков на двух костях равна 1/6. Два события, которые не могут происходить одновременно, называются взаимоисключающими. Например, при однократном бросании игральной кости 5 очков и 6 очков одновременно выпасть не могут. Вероятность того, что произойдет одно или другое взаимоисключающее событие, равна сумме вероятностей этих событий. Например, вероятность того, что при однократном бросании кости выпадет либо 5, либо 6 очков, равна 1/6 + 1/6 = 1/3.
Вероятность достоверного события (которое заведомо наступит) принимается равной 1, а вероятность события, наступление которого невозможно, считается равной 0. Очевидно, что наступление и ненаступление данного события взаимно исключают друг друга, а потому, если вероятность наступления какого-нибудь события равна p, то вероятность его ненаступления будет 1 — p. Однако в более сложных задачах, когда число возможных исходов бесконечно велико, вероятность нельзя задать с помощью простого перечисления всех возможных случаев. Например, если мы представим себе испытание, состоящее в бесконечной серии бросаний симметричной монеты, то ситуация, когда во всех бросаниях выпадают только «орлы», в принципе не невозможна, хотя такому исходу необходимо приписать вероятность, равную 0, так как в высшей степени «невероятно», чтобы в любой достаточно длинной серии бросаний выпадали только «орлы». Для детального анализа вероятностных задач, более сложных, чем простые азартные игры, необходима более строгая и абстрактная формулировка. Именно она и будет рассмотрена ниже.
Основной принцип комбинаторного анализа гласит: если что-либо одно можно осуществить m способами, а нечто другое — n способами, то эти действия последовательно можно осуществить mґn способами. [...]Например, Четверых людей можно выстроить в ряд 4*3*2*1 = 24 способами, так как первого можно выбрать 4 способами, второго — 3 способами, третьего — 2 способами, а четвертого — только одним. Но четырех людей можно посадить в четыре автобуса 4*4*4*4 = 256 способами, так как каждый из них может сесть в любой из четырех автобусов.
Перестановки и сочетания. Многие задачи теории вероятностей удается проанализировать, если воспользоваться некоторыми следствиями из приведенного выше комбинаторного принципа. Размещение предметов в определенном порядке называется перестановкой этих предметов. Например, существуют шесть перестановок чисел 1, 2, 3, а именно: 1, 2, 3; 1, 3, 2; 2, 1, 3; 2, 3, 1; 3, 1, 2; 3, 2, 1. Число перестановок из n предметов равно 1*2*3*… *n. Сокращенно это число записывается как n! (и читается как «факториал числа n» или «n факториал»). Любое размещение предметов, порядок которых не имеет значения, называется сочетанием. Из набора чисел 1, 2, 3, 4, 5 можно извлечь десятью различными способами любые два числа, если мы условимся не различать пары, состоящие из одних и тех же чисел, взятых в различном порядке, т.е., например, не различать 1, 2 и 2, 1. Если из двенадцати человек нужно выбрать комитет в составе девяти членов, то это можно сделать столькими способами, сколько сочетаний из двенадцати по девять мы можем составить. Это, естественно, относится к случаю, когда сам порядок размещения членов внутри комитета несуществен. Однако число разных баскетбольных команд, которые можно составить из тех же двенадцати человек, равно числу перестановок из девяти элементов, которые можно набрать из этих двенадцати, так как в баскетбольной команде каждый игрок имеет свой номер. Вторая задача для анализа проще: существуют 12*11*10*9*8*7*6*5*4 перестановок, так как первый номер можно выбрать 12 различными способами, второй номер — 11 способами и т.д., пока мы не дойдем до последнего, девятого, номера, который может быть выбран четырьмя способами. В первой задаче любая из 9! перестановок девяти членов комитета приводит к одному и тому же составу комитета, так как состав комитета не зависит от того, в каком порядке перечислять его членов; иначе говоря, число перестановок 12*11*10*9*8*7*6*5*4 дает ответ, который в 9! раз больше, чем нужно. Следовательно, число сочетаний из двенадцати человек по девять равно указанному произведению, деленному на 9!, или
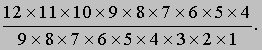
=220. В общем случае число сочетаний из n по r равно n (n — 1)(n — 2)… (n — r + 1)/r! или n!/r!(n — r)! Это число называется биномиальным коэффициентом
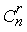
Еще один полезный принцип состоит в утверждении, что n предметов можно разложить в r коробок rn различными способами, если в любой коробке может находиться любое число предметов.
Обратимся теперь к некоторым приложениям этих принципов. 1) Какова вероятность выпадения ровно двух шестерок при пяти бросаниях игральной кости (или, что то же, при одном бросании пяти костей)? Пять костей могут выпасть 65 способами. Две кости, на которых выпали шестерки, можно выбрать способами (сочетания появляются потому, что порядок, в котором выпадают шестерки, несуществен), т.е. (5*4*3*2*1)/((2*1) * (3*2*1)) = 10 способами. Нешестерки (их 5: 1, 2, 3, 4 и 5 очков) на остальных 3 костях могут выпасть 53 способами. Следовательно, мы получаем ровно две шестерки из пяти бросаний 10*53 способами; искомая вероятность, таким образом, равна 10*53/65 или 1250/7776, т.е. ок. 1/6.
2) Какова вероятность получить ровно два туза, если из колоды, состоящей из 52, извлекаются 5 карт? Извлечь из колоды 5 карт можно способами. Пять карт, из которых два туза, а остальные три — нетузы, можно получить, извлекая два туза способами, а три нетуза — способами. Искомая вероятность равна
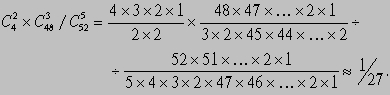
СОВРЕМЕННАЯ ТЕОРИЯ ВЕРОЯТНОСТЕЙ
Современная теория вероятностей, подобно другим разделам математики, например геометрии, состоит из результатов, выводимых логическим путем из некоторых основных утверждений, или аксиом, и приложений к ситуациям в реальной жизни, относительно которых предполагается, что они согласуются с аксиомами. Трудность теории вероятностей заключается в том, что объекты, составляющие предмет ее изучения, носят гораздо более общий характер и поэтому не столь наглядны, как, например, объекты геометрии или механики. Теория вероятностей занимается изучением событий и их вероятностей, представляемых числами, заключенными в интервале от 0 до 1. В случае исторически знаменитых задач, связанных с азартными играми, можно интуитивно понять, как должна быть сформулирована соответствующая математическая задача. Такая задача обычно имела следующий вид: заданы вероятности некоторых элементарных событий; требуется вычислить вероятность какого-нибудь более сложного события, связанного с элементарными событиями некоторым простым образом. Прежде чем мы более подробно представим современную теорию, полезно проиллюстрировать интуитивную теорию и ее методы на примере. Вычислим вероятность того, что некоторому игроку в бридж достанется один или несколько тузов. В качестве элементарных событий удобно рассматривать получение на руки возможных вариантов из 13 карт. Необходимо, чтобы распределение вероятностей между наборами имеющихся у игроков карт, т.е. элементарными событиями, отражало наше убеждение в том, что карты сдавались весьма специальным образом, а именно случайно. Постулат, который мы примем, сводится к определению того, что мы понимаем под случайной сдачей карт. Мы постулируем, что любой набор из 13 карт, который может достаться игроку при раздаче, равновероятен. Какова эта вероятность? Ответ на этот вопрос может дать интуитивно очевидный принцип, служащий основным методом теории вероятностей: если имеется несколько взаимоисключающих событий (таких, что каждый раз происходит только одно из них), то вероятность того, что произойдет по крайней мере одно из них, равна сумме вероятностей каждого из событий в отдельности.
Кроме того, потребуем, чтобы вероятность события, которое заведомо происходит, была равна единице. Сделанные замечания позволяют решить нашу задачу. Пусть n — число различных вариантов наборов карт, которые может получить игрок, A1, A2, ..., An — события, соответствующие получению каждого из этих наборов, и P(A1), P(A2), ..., P(An) — вероятности этих событий. Пусть A — событие, состоящее в том, что игрок получает набор карт, содержащий один или несколько тузов, и m — число наборов из 13 карт, каждый из которых содержит один или несколько тузов, B1, B2, ..., Bm — события, соответствующие получению такого набора. Тогда A — событие, состоящее в том, что наступает одно из множества событий B1, B2, ..., Bm. Наконец, пусть P (A) — вероятность события A. Так как события A1, A2, ..., An равновероятные и взаимоисключающие, причем одно из них достоверно происходит, то
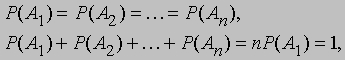
и, следовательно,
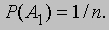
Аналогично,
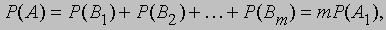
в силу чего окончательно получаем
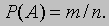
Этот результат сводит исходную задачу к чисто комбинаторной задаче нахождения чисел m и n. Последняя легко решается с помощью теории перестановок и сочетаний, некогда бывшей существенной частью теории вероятностей, но ныне таковой не являющейся. Число n есть просто число способов, которыми можно выбрать 13 карт из 52. Используя стандартные обозначения, находим
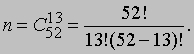
Вместо числа m проще найти число (n — m) — число наборов из 13 карт, не содержащих ни одного туза, или число способов, которыми можно выбрать 13 карт из 48:
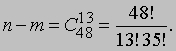
Следовательно,
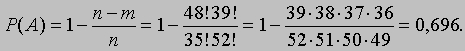
Было бы ошибкой полагать, что решение любой вероятностной задачи всегда можно представить в виде простого отношения двух чисел вида P (A) = m/n. Приведенное рассуждение показывает, что такое отношение (числа благоприятных случаев к общему числу случаев) выражает вероятность, которую требуется найти, если элементарные события равновероятны.
По-видимому, наиболее важной ситуацией, в которой изложенный выше метод неприменим, является биномиальное распределение вероятностей. Представим себе, что некоторое испытание проводится n раз, причем каждый раз его исход может быть либо благоприятным У («успех»), либо неблагоприятным Н («неудача»). Элементарными событиями можно считать все возможные последовательности У и Н (их общее число равно 2n), каждая такая последовательность содержит n символов. В этом случае вероятности элементарных событий невозможно вывести из постулата о равновероятности всех последовательностей из n символов, содержащих одинаковое количество У и Н. Их невозможно получить и из дополнительного постулата о том, что вероятность отдельного благоприятного исхода равна p, а вероятность одного неблагоприятного исхода равна 1 — p. Необходимо также в явном виде указать, каким образом вероятность будущих исходов испытаний зависит от прошлых исходов.
Простейшее предположение состоит в том, что будущие исходы не зависят от прошлых, что довольно часто встречается на практике.
Его можно формально выразить, постулировав, что вероятность любой заданной последовательности У и Н равна произведению вероятностей отдельных исходов. При таких предположениях вероятность, например, последовательности исходов УУУНУНН равна p4(1 — p)3. Нетрудно показать, что в общем случае вероятность получения ровно k благоприятных исходов в n испытаниях равна
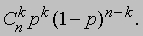
Вся статья http://dic.academic.ru/dic.nsf/enc_colier/6347/ВЕРОЯТНОСТЕЙ
159 |
Читайте на SMART-LAB:

Снижение военной премии в нефти: что это меняет для доллара и G10
Во второй половине понедельника – начале вторники рынки активно пересматривают премию за худший сценарий на энергетическом рынке, что цепочкой...
16:32

Время возвращаться к валюте?
Относительно рубля я давно придерживаюсь логики, что, пока эксперты предрекают ему неизбежное ослабление, можно за рубль не очень...
07:00
теги блога Мурен(а)
- brent
- eurrub
- eurusd
- forex
- forts
- gold
- karapuz
- MetaTrader 5
- micex
- moex
- mt5
- quik
- RI
- rts
- Si
- sugar
- sugr
- TradingView
- USDRUB
- ut
- акции
- бан
- банк
- банки
- биржа
- бкс
- брокер
- брокеры
- валюта
- видео
- волны вульфа
- вопрос
- встреча smart-lab
- втб
- втб брокер
- втб24
- газпром
- герчик
- ГО
- Доллар рубль
- золото
- ИИС
- инвестирование
- инвестиции в недвижимость
- интервью
- книга
- книги
- конференция смартлаба
- кредит
- кризис
- личные деньги
- личные фонды
- лчи
- ммвб
- мобильный пост
- мосбиржа
- Московская биржа
- налоги
- Налогообложение на рынке ценных бумаг
- натуральный газ
- недвижимость
- нефть
- норникель
- облигации
- обучение
- Олейник
- опрос
- опцион
- опционы
- Открытие
- открытие брокер
- офз
- ОФЗ облигации
- оффтоп
- охота на герчика
- психология
- пшеница
- рбктв
- рецензия на книгу
- ртс
- русгидро
- сахар
- сбербанк
- смартлаб
- срочный рынок
- суд
- технический анализ
- тинькофф
- торговые сигналы
- торговый софт
- трейдинг
- финам
- Финансовая грамотность
- форекс
- ФОРТС
- фьючерс РТС
- фьючерс РТС
- ФЬЮЧЕРСЫ
- швагер
- юмор





















например, в задаче со стрельбой нелинейный эффект такого влияния может сказываться при быстром износе ствола… (Кстати, для скорострельных МЗА совсем не пустой звук когда тыщу другую выстрелов за несколько минут расстреляют, то к концу характеристики ствола явно «плывут», что вполне конкретно влияет на дальность полёта/траекторию снаряда...)
Коломогоров А.Н. Основные понятия теории вероятностей. М., 1974 Ширяев А.Н. Вероятность. М., 1980 Феллер В. Введение в теорию вероятностей и ее приложения, тт. 1-2. М., 1984 Прохоров Ю.В., Розанов Ю.А. Теория вероятностей. М., 1987
Я ж говорю — глаз режет МНЕ. Поэтому и написал. Ну а на вкус и цвет… В МГУ предмет и кафедры именовались именно так — Теория ВероятностИ.
Но ведь На рынке вероятность не в том угадаешь или нет а в том что При наличии тренда и совершения по мере его развития правильных сделок можно получить часть прибыли этого тренда с определенными рисками.
И вероятность сводится к двум моментам:
1.с какой вероятностью подойдет твоя стратегия к движению данного тренда.
2.С какой вероятностью в боковике ты потеряешь меньше чем заработаешь в тренде.