SMART-LAB
Новый дизайн
Мы делаем деньги на бирже
Информация
Блог им. bstone
Прокачка ласкового зигзага
- 12 июля 2018, 15:56
- |
Берем предположительно ласковый зигзаг в сентябрьской серии: продаем 105-й пут и покупаем 125-й кол.
Насколько он ласковый? Это легко посчитать. Для этого надо всего лишь угадать реализованную волатильность БА на момент квартальной экспирации :)
Тут у многих возникают сложности, поэтому я сделаю это за них. В духе «почтенных» аналитиков, я объявлю, что волатильность пойдет либо вверх, либо вниз, но в целом вполне себе может оказаться в диапазоне от 16.8% до 23%.
Дальше уже проще. Т.к. мы продаем пут и покупаем кол, то даже целому поколению опционных гениев, взращенному на просторах Смарт-лаба, должно быть понятно, что хеджировать кол надо по 16.8%, а пут по 23%. Если не понятно, то никакие они еще не гении и надо еще подучиться.
Считаем теперь насколько все-таки ласковый наш зигзаг. Я считал в 14:09 и фьюч был на отметке 116740. Получилось 5.74 пункта — все, что добавит к вашему финрезу хеджирование по БШ.
Курам на смех! Нужно срочно звонить в сервис по прокачке зигзагов… к счастью обеденный перерыв уже закончился и удача не заставила себя долго ждать. Ласковость зигзага после прокачки — 262.52 пункта. Или другими словами в 46 раз больше. Мое почтение!
Ниже в графическом виде. На нижнем графике дельты, по которым хеджируем. Синяя — прокачанная, красная — родная Блэковская.
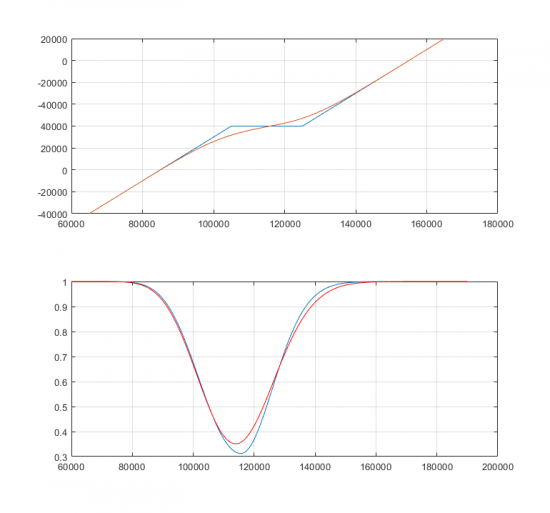
Прикольно? Конечно, но не стоит забывать, что в итоговый финрез входит еще и отличие рыночной стоимости опционов от теории на наших границах ожидаемой RV. На момент, когда я прикидывал, хитрая дельта давала увеличение финреза в 7 раз.
Это не 46, конечно, но вы подойдите к первому встречному на улице и скажите: «Увеличьте профит моего зигзага в 7 раз!»… вам никто не увеличит :)
Насколько он ласковый? Это легко посчитать. Для этого надо всего лишь угадать реализованную волатильность БА на момент квартальной экспирации :)
Тут у многих возникают сложности, поэтому я сделаю это за них. В духе «почтенных» аналитиков, я объявлю, что волатильность пойдет либо вверх, либо вниз, но в целом вполне себе может оказаться в диапазоне от 16.8% до 23%.
Дальше уже проще. Т.к. мы продаем пут и покупаем кол, то даже целому поколению опционных гениев, взращенному на просторах Смарт-лаба, должно быть понятно, что хеджировать кол надо по 16.8%, а пут по 23%. Если не понятно, то никакие они еще не гении и надо еще подучиться.
Считаем теперь насколько все-таки ласковый наш зигзаг. Я считал в 14:09 и фьюч был на отметке 116740. Получилось 5.74 пункта — все, что добавит к вашему финрезу хеджирование по БШ.
Курам на смех! Нужно срочно звонить в сервис по прокачке зигзагов… к счастью обеденный перерыв уже закончился и удача не заставила себя долго ждать. Ласковость зигзага после прокачки — 262.52 пункта. Или другими словами в 46 раз больше. Мое почтение!
Ниже в графическом виде. На нижнем графике дельты, по которым хеджируем. Синяя — прокачанная, красная — родная Блэковская.
Прикольно? Конечно, но не стоит забывать, что в итоговый финрез входит еще и отличие рыночной стоимости опционов от теории на наших границах ожидаемой RV. На момент, когда я прикидывал, хитрая дельта давала увеличение финреза в 7 раз.
Это не 46, конечно, но вы подойдите к первому встречному на улице и скажите: «Увеличьте профит моего зигзага в 7 раз!»… вам никто не увеличит :)
теги блога bstone
- Intraday
- LUA
- Ri
- SR
- Аллирог
- аналитик
- аналитика
- биржа
- Блэк-Шоулз
- бонус
- брокеры
- вероятность
- визуализация сделок
- Волантильность
- волатильность
- волны эллиота
- Волотильность
- герчик
- демо форекс
- депо
- депозит
- Дискреционный трейдинг
- ДУ
- интрадей
- книга
- Книги
- Коровин
- короткий стоп
- кризис
- кукл
- лчи
- лчи 2015
- Маркидон
- мобильный пост
- Нефть
- опрос
- опцион
- опционы
- опыт
- открытие брокер
- оффтоп
- просадка
- психология трейдинга
- развод
- рецензии
- рецензия
- риск
- роботы
- рублебакс
- рынок
- Сбер
- сбербанк
- Сбой на бирже
- сделки
- семинар Герчика
- си
- скальп
- слив
- смартлаб
- стакан
- стоп
- Стоп-лосс
- ТА
- технический анализ
- торговые роботы
- трейдер
- трейдинг
- улыбка волатильности
- уровни
- шорты
- Эллиот
- юмор
Картинка последняя понравилась
Недавно по ящику фильм показывали «Код да винчи», там этой картинкой женщин изображали, а мужчин, наоборот, обратной выпуклостью.
Напоминает защиту Алехина, вариант 4 пешек.
понял.
Осталось только детали, технику.
Основной вопрос хеджировать БА ботом (что просто — задать внутренний и внешний канал ;-))) или добором опцев (что хитро и возможно ли для смертного?)
у меня хедж пока получался баснословно дорогой для моего депо…
Я думаю, хеджировать БА — просто, но тупо и не прокатит.
А вот греками — тут надо очень разумный бот… так как там ликвидность давит…
и зажмут к экспире, нервы сдадут у «бота»…
Про разную волу говорят: просто чтобы не остаться без трусов.
Хотелось бы лучше понять глубокую мысль: зачем купленный колл хеджировать по 17%? Тогда уж логичней выглядит хедж длинных по 23?
Стас Бржозовский, что думаешь насчет этой чудесной идеи «смазывать разные ноги разным кремом»?
bstone, давайте совсем просто? Один опцион, центральный колл, куплен. Допустим, купили мы его по 20%.
Если делать хедж по 23%, то распространенное мнение состоит в том, что это принесет прибыль эквивалентную 3% по воле. Потому что ДХ в данном случае — это синтетическая продажа опциона.
Поэтому мы должны делать ДХ по высокой воле, а покупать по низкой.
Нет?
Если просто, то лучше вообще на пальцах:
Если мы продали опцион, то теряем деньги при каждом рехедже, поэтому нам выгодно рехеджить как можно меньше, в идеале никогда, т.е. по бесконечной воле, но кто у нас купит по такой?
Если купили, то наоборот — мы плюсуем при каждом рехедже и нам выгодно это делать как можно чаще, в идеале по нулевой воле. И опять, жаль никто по ней не продает :)
В таком случае просто получится направленная позиция, итоговый результат будет зависеть от того по какой цене экспирируется БА.
А вот можно ли этот вывод экстраполировать на разные страйки неясно.
bstone, это обычный арбитраж на колл-пут паритете тогда.
Коллегу интересует можно ли запустить два дельта-хеджера с разными параметрами и наслаждаться при этом прибылью? =)
bstone, обычно хеджируют или по той айви, по которой опционы купили, или хеджируют по текущей исторволе. Но все опционы одинаково.
Третий подход состоит в том, что мы управляем хеджем не параметром "волатильность хеджа", а просто смотрим на позицию и как только ее дельта стала большая (по модулю) — выравниваем. В этом подходе управление хеджем идет косвенно через управление параметрами той улыбки, по которой вычисляется профиль позиции.
Назначать каждому опциону свою волатильность для хеджирования — это совсем свежий взгляд на вещи. Хочется понять его до конца.
Но у меня тут суть в другом. Конкретно в том, что мы смотрим на вещи как они есть: никто не знает какая будет RV. Что более правдоподобно? Что она окажется равной текущей IV, текущей HV, или все-таки окажется в некотором диапазоне вокруг их значений? Очевидно же, что последнее.
Как оценить результат от ДХ в условиях неопределенности RV? Самое очевидное — это считать его по БШ, подставляя туда минимальную/максимальную границу RV. В результате получаются диапазоны значений для каждой цены БА. Фактически два профиля стоимости.
Какой из них брать? Естественно нижний, т.к. рассчитывать на наилучший возможный результат самоубийственно. Поэтому ДХ по меньшей воле для покупок и наоборот.
Но это мы только говорим о гарантированной стоимости ДХ по БШ, т.е. до прокачки. Самое интересное начинается дальше, когда мы прокачиваем модель ценообразования опциона, вшивая туда факт неопределенности RV. Тогда в модели получается нелинейное уравнение. И вот это очень круто, потому что эта нелинейность означает, что финрез портфеля больше не равен сумме финрезов его частей.
Линейной суперпозиции больше нет. Вместо нее есть нелинейные эффекты и возможны комбинации, когда результат суммирования опционных позиций оказывается больше суммы их результатов по отдельности :)
bstone, великая сила Коллективный Разум: вроде бы, никто ничего вразумительного сказать не может и аргументация на уровне «мамой клянусь». А какая-то ценная мысль нет-нет да и проскочет в башке.
Премного благодарен Вам за тему!
А до вечного двигателя тут очень далеко. Например в сентябрьской серии сейчас даже прокачанные зигзаги не дают прибыли, если закладываться на указанный диапазон RV. Нужно либо его сужать, но тогда его достоверность падает, либо ждать пока IV упадет до 18% хотя бы.
Причем я хочу подчеркнуть, что речь идет о гарантированной прибыли при условии, что RV окажется в целевом диапазоне. Поэтому все весьма скромно, если сравнивать с вечным двигателем :)
Когда же применяется прокачанная модель, то понятия волатильности опциона/портфеля там уже нет. Там есть верхняя и нижняя граница RV и дельта считается так, чтобы обеспечить минимальное приращение стоимости портфеля на каждом шаге хеджирования в условиях неопределенной волатильности. Поэтому расчетная стоимость портфеля является пессимистической, т.е. она гарантирована независимо от того, какой окажется в итоге RV, лишь бы не вылезла из расчетного диапазона.
Добавлю еще пару измышлений для контекста.
Посмотрим с другой стороны. Пусть мы просто хотим покупать недельный опцион и держать его каждый раз до экспирации. Скажем также, что мы знаем, что RV базового актива все время будет 20%. Теперь вопрос, будем ли мы покупать опцион, если нам его будут все время предлагать по 23%? Очевидно, что нет, т.к. мы знаем, что справедливой ценой будет 20% и в долгосроке мы тупо будем терять в среднем 3%.
Теперь скажем, что RV не постоянна, а колеблется в диапазоне от 15% до 25%. По какой цене мы готовы покупать тот же опцион, чтобы гарантированно не получить отрицательное матожидание? Должно быть очевидно, что нам надо прайсить по меньшей границе. Так ведь? Т.е. для расчета максимальной стоимости, по которой мы готовы купить, мы будет считать стоимость ДХ по 15% воле? Согласны?
Теперь другой срез. Как я уже говорил, внутри прокачанной модели, мы ведем расчет стоимости портфеля на каждом шаге интегрирования пессимистически, чтобы посчитать минимальный финрез портфеля в предположении, что RV может оказаться любая в пределах заданного диапазона.
А это значит, что на каждом шаге мы предполагаем, что волатильность принимает значение, при котором наш портфель увеличивается на наименьшую величину. Поэтому если в простейшем случае у нас куплен один опцион, то мы предполагаем, что волатильность минимальна. Если продан — максимальна. Логично?
Для портфеля опционов мы смотрим на знак гаммы портфеля, и если гамма положительна, берем меньшую волатильность. Если же гамма отрицательна, то берем большую волатильность, т.к. умноженная на отрицательную гамму она даст нам наименьшее приращение портфеля в сравнении с меньшей волатильностью.
Дисперсия результатов без хеджа будет значительно выше, но в достаточно длинной серии покупок опционов без хеджа, результат будет равен покупкам с хеджем, то есть МО с ДХ будет равно МО без ДХ. (Если не принимать во внимание риски повышения ГО и веги, конечно)
Aphelion, да, смысл ДХ именно в снижении дисперсии финреза.
Ну и в арбитраже между ашви/айви. =)
ДХ — это де-факто синтетический опцион. У него есть своя «реализованная стоимость».
Если формула БШ верна, и волатильность опциона была правильно оценена продавцом в каждой сделке, то итоговый результат серии должен быть равен нулю, вне зависимости от того хеджил покупатель дельту или нет. (И вне зависимости от волы по которой считалась дельта)
Согласен, что ДХ — по сути опцион. Вопрос в том, влияет ли вола, по которой идет ДХ на его реализованную стоимость в серии сделок и соотвественно на мат. ожидание всей позиции.
Собственно, весь вопрос ветки, хедж опционов по разной воле это грааль или нет. Мне кажется, что нет, но если вдруг окажется, что грааль, то хоть завтра приму на вооружение =)
Как переложить 1 концерт Чайковского для фортепиано с оркестром для балалайки…
Маленький мальчик в зоопарке пролез в клетку со львом и протянул ему печеньку. Ну что тут сказать, мальчик хотел покормить льва — мальчик покормил льва.
тут как бы, в результате нелинейности клетки мальчик вышел с 2 мя печеньками, а львов стало 1,5.
Ох уж эти подсчеты недобытого финреза…