талеб

Талеб в разных вариантах упоминал что варианс использовать нельзя, потому что ее нельзя точно измерить. И как следствие GARCH который основан на измерении варианс использовать нельзя. Меня это заявление беспокоило, поскольку я гарч использую, и несколько недель в фоне размышлял.

For silver, in 46 years 94 percent of the kurtosis came from one single observation. We cannot use standard statistical methods with financial data. GARCH (a method popular in academia) does not work because we are dealing with squares. The 52 a non-technical overview — the darwin college lecture variance of the squares is analogous to the fourth moment. We do not know the variance. But we can work very easily with Pareto distributions. They give us less information, but nevertheless, it is more rigorous if the data are uncapped or if there are any open variables. // Statistical Consequences of Fat Tails

Я думаю он прав и не прав одновременно. Прав что использовать варианс в чистом виде, как статистику по r^2 походу реально смысла нет, вот как она выглядит (картинка1).

( Читать дальше )

Закончил чтение манифеста Нассима Талеба — Черный лебедь и решил изложить, что интересного я почерпнул для себя, как для внутридневного трейдера.

Скажу сразу, что я не могу однозначно относиться к трудам Н. Талеба. Многие моменты мне близки, некоторые не очень, но более всего мне интересен тот факт, что он близко общался с Бенуа Мандельбротом.

“Профессиональный бизнесмен, которому не удалось обеспечить каждого вкладчика неким эквивалентом счастливого лотерейного билета, наверняка будет думать, что “допустил ошибку”, — или, хуже того, что “были допущены ошибки”. Он будет раскаиваться в своей “непродуманной” инвестиционной стратегии. Единственный действенный способ избавиться от этой непрестанной головной боли — принять случившееся как неизбежность.”

Учитывая свой жизненный и торговый опыт, данная фраза очень запала мне в душу. По данной проблеме Н. Талеб рекомендует завести дневник. 

“Отсутствие результатов ценно само по себе, так как оно приближает вас к открытию: теперь вам известно, где не нужно искать!”

( Читать дальше )

Для лог доходности акций r = log S_T/S_0 степень хвоста не зависит от периода, прибыль за день, месяц или год.

Это видно математически Pr(X>x) ~ Cx^-a — степень a сохраняется при агрегировании (суммировании), меняется лишь константа.

И на графиках log log правого хвоста > 0.97 квантили, цвет дециль волатильности (множественные линии одного цвета — когорты чтобы избежать overlapping bias). Наклон на всех периодах одинаковый.

Проблема с которой я столкнулся в прошлых постах, при попытке определить степень тяжести хвостов распределения EVT Peak Over Threschold эстиматор дает огромные ошибки.

Если рассмотреть идеальный случай:

[1 / fit(GeneralizedPareto, rand(GeneralizedPareto(0, 1, 1/3), 500)).ξ for _ in 1:10]

получим

2.3747
 3.4744
 2.9658
 2.3281
 4.3979
 2.7633
 3.3022
 4.7440
 2.6349
 2.9094

И это при а) идеальном совпадении структуры (форма кривой), б) гиперпараметров (трешхолда=0), и в) достаточно большого сэмпла 500 точек, что не всегда возможно при «изоляции» хвоста (x > u) на реальных данных, обычно трешхолд ~ 0.98-0.99 квантиль, соотв чтобы получить хвост 500 точек нужен сэмпл 25к.

И даже в таком идеальном случае, ошибки 2.4-4.7. Ну а когда эти условия не идеальные — ошибка больше, что мы и наблюдали на графиках в прошлых постах.

Вывод — эстиматоры POT GPD MLE а также WM — совершенно не применимы на практике, и почему об этом не говориться на первой же странице книг и статей по EVT, чтоб не тратить на них время и сразу переходить к другим -  непонятно (либо я все еще допускаю где то ошибку, но я ее не вижу...)

( Читать дальше )

Я столкнулся с проблемой — самый точный (в теории) метод оценки экспоненты хвоста распределения давал совершенно дикие результаты smart-lab.ru/blog/1188320.php Мне кажется я нашел причину почему. Он действительно ошибается.

Даже при сэмпле 100к StudentT(df=4) он в половине случаев не может точно определить экспоненту хвоста, у него сильная системная ошибка, биас, MLE фиттинг систематически недооценивает хвост, и получается как на картинке (это лог лог CDF правого хвоста, >0.99 квантили). 


Фиттинг сделан верно, получилась некая «средняя» (точнее MLE) линия проходящая по всем точкам, и которая систематически недооценивает экспоненту.

И становится понятно эмпирическое правило «выкинуть последние 5-10 точек» — точнее, это правило неверное, если просто выкинуть случайно несколько последних точек результат буде вообще дикий, видимо в этом правиле есть упущенное дополнение, что выкидывать нужно не просто случайно точки, а только последние точки которые пошли вниз.

P.S. Как это сделать автоматически — может выкинуть последние точки, как вариант — нужно итерационно делать фиттинг, и выкидывать последнюю точку до тех пор пока df растет, а как только он упал сразу остановиться. Или, попробовать другие эстиматоры кроме MLE…

( Читать дальше )

Недавно потребовалось установить экспоненту Парето хвоста распределения вероятностей. И чтобы посмотреть насколько хорошо методы EVT работают, я сделал простой пример.
Пример: 30 сэмплов StudentT(df=4), каждый размером 20000. Определить экспоненту хвоста используя методы: Хилла, GPD, LeastSquares, CDF LogLog PLot.
Результаты ужасны: точность всех методов плюс минус километр. Я не вижу ни малейшего смысла в EVT поскольку вручную по линейке установить наклон линии на ЛогЛог Графике CDF оказывается не хуже (мне кажется даже лучше) чем специализированные методы EVT.
На графике — y — найденная экспонента хвоста, каждая линия это отдельный сэмпл, цвет метод определения, х — гиперпараметр (число точек в хвосте распределения которые использовались в расчетах). Верный результат это горизонтальная линия y=4, вместо этого мы наблюдаем, в зависимости от метода — систематические ошибки, либо дикий хаос.


Даже, мне кажется с линейкой предпочтительней, график лог лог. Поскольку ты боль менее визуально и интуитивно понимаешь что делаешь. 

( Читать дальше )

Много методов: Hill, EVT GPT, регрессия. И все с точностью километр. На графике — 30 симуляций: 30 сэмплов StudentT(df=4) 20к, для каждого сэмпла определяется df различным эстиматором (цвет линии), ось х — значение трешхолда эстиматора. 


Правильный результат — постоянная линия с y=4. Единственный нормальный результат (красные линии) это MLE полного распределения, но это именно что эстиматор полного распределение, а не Tail Estimator. Среди хвостовых эстиматоров ни одного хорошего.

EVT GPT на который я больше всего расчитывал (синии линии), вообще ничего не измеряет (но возможно я допустил ошибку и неверно его считаю, по идее он должен быть самый точный).

Подробней www.reddit.com/r/nassimtaleb/comments/1mdwqjw/huge_errors_in_heavy_tail_estimators_hill_evt_gpt/
Код gist.github.com/al6x/11e66ab92c525f2ef2c1510e6ac7a3f7

Это последний, третий пример применения закона нормального распределения (предыдущие примеры объясняют распределение людей по финансовой грамотности и по отношению к воровству).

Нассим Талеб в книгах “Одураченные случайностью”, “Чёрный лебедь” и “Антихрупкость” разработал и описал концепцию жирных или толстых хвостов гауссовой кривой.

С точки зрения действия законов статистики существует две противоположные страны: Среднестан и Крайнестан.

В первой главенствует нормальное распределение вероятностей, то есть высоковероятные события главенствуют (горб на графике), а маловероятные случаются редко (края графика с обеих сторон).

К примеру, такие массовые профессии, как бухгалтеры, кассиры, рабочие, охранники, врачи, учителя, можно отнести к Среднестану. Здесь шансы добиться огромного дохода минимальны, так как есть естественные ограничения масштаба деятельности, но заработать на кусок хлеба в этих профессиях удастся практически в любом случае. Родители в советах детям часто руководствуются житейским принципом «лучше синица в руке, чем журавль в небе».

( Читать дальше )

Как говорил герой Макконахи в “Волк с Уолл-Стрит” — “новые ситуации, новые акции”.
Итак, основа моего американского портфеля — VOO, т.е. etf на S&P500. Растет со всем рынком, падает тоже со всем рынком.

Конечно, есть акции/фонды, которые приносят жирные дивиденды, например BTI (дивдоха 9.69%), PDI (дивдоха 16.65%) и другие.
Есть банки (купленные на заливе в прошлом году), есть и полупроводники — NVDA, AMD, TSM итд, есть фарма — NVO, PFE, есть технологичные монстры вроде TSLA, AMZN итд.

Новая идея — регулярная покупка индекса на 100 самых популярных технологичных акций, т.е. NASDAQ-100. Был выбор, что покупать — QQQ (старейший индекс) или QQQM (более новый аналог старейшего индекса, стоит дешевле и чуть ниже комиссия).

Для себя выбрал QQQM. Буду покупать его несколько раз в год по текущим ценам. Некоторые аналитики считают, рынок неоправданно дорогой, особенно технологический сектор. Еще вот-вот и рухнет.
Посмотрим! Буду регулярно делиться информацией, что происходит с портфелем. Как сказал бы Талеб — “шкура в игре”.

( Читать дальше )

Антихрупкость и ассиметрия – ключевые понятия Талеба в контроле над «жирными хвостами» рисков. Хвостовой риск (tail risk) — риск наступления редкого события, в результате которого цена актива за короткое время изменится больше, чем на три стандартных отклонения от среднего значения. Черные лебеди кроются именно за пределами 3-х отклонений (сигм).

Нормальное распределение и хвостовой риск

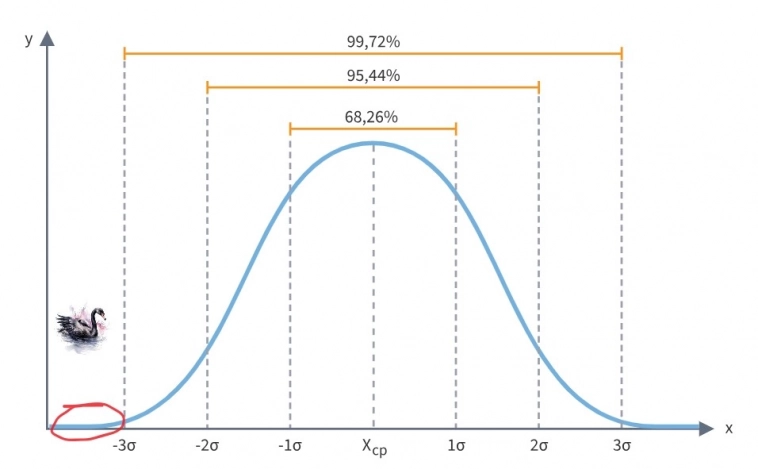
Правило 3-х сигм заключается в том, что при нормальном распределении случайной величины, к которой можно отнести доходность на рынке акций, 68,26% значений лежат в пределах 1-й сигмы, 95,44% — в пределах 2-х сигм, а 99,72% — в пределе 3-х сигм в любую сторону от среднего значения. Вероятность того, что величина выйдет за пределы 3-х сигм составляет всего 0,28% или 300 к 1.

Распределение доходности S&P500 за 150 лет

( Читать дальше )