SMART-LAB
Новый дизайн
Мы делаем деньги на бирже
Блог им. tashik
Делаем опционный калькулятор по биномиальным моделям оценки в Google Spreadsheet (часть 1)
- 06 ноября 2021, 17:18
- |
Модель Блэка-Шоулза, став де-факто индустриальным стандартом оценки опционов, успела навязнуть в зубах. Поэтому в этот славный выходной день мы побалуем себя альтернативным вариантом оценки — на основе моделей на базе биномиальных деревьев. То, что мы в итоге создадим, будет работать для наших маржируемых опционов американского типа с базовым активом-фьючерсом.
Суть биномиальной модели оценки в том, что при тех же вводных, что и у Блэка-Шоулза, она строится на разбиении времени до экспирации на равные временные интервалы (отрезки) (а в МБШ время непрерывно), и движение цены от начала одного отрезка к началу другого может быть либо вверх, либо вниз. Модель упрощает реальность ещё и тем, что в процентах шаг движения цены вверх и шаг движения цены вниз на всех отрезках одинаков, при этом шаг вверх может быть не равен шагу вниз. Размер шага вверх и шага вниз рассчитывается моделью из входных данных. Вероятности на следующем отрезке двигаться вверх или вниз также рассчитываются моделью из входных параметров и так же неизменны. Необязательно это будут вероятности 50/50, может получиться любое соотношение в сумме, дающее 100%.
Критикой моделей и их базовых предпосылок мы тут заниматься не будем. Мы тут будем опционный калькулятор писать.
Открываем Google Spreadsheets (MS Excel тоже подойдет, но у меня лапки MacOS, и Excel у меня там не имеется), создаем новый документ. Первый лист его будет представлять «морду» нашего калькулятора и содержать поля для входных параметров и поле для отображения результата расчета. Самое время эти входные параметры перечислить — вот таким образом (ВНИМАНИЕ! номера строк и буквы столбцов будут дальше иметь значение):

Как видите, ничего незнакомого среди входных параметров нет. Волатильность — которая и есть по сути наша ставка, за которую нам платят и с нас берут) — как параметр модели есть, как и в МБШ.
Результат расчета будет выведен в ячейку B13.
Поименуем ячейки, чтобы было проще писать и читать формулы. Я решила остаться в привычной по БШ нотации, где S — текущая цена БА, sigma — волатильность, K — страйк, T — время до экспирации. Для типа опциона буду использовать имя CallPut, для вида опциона (американский или европейский) — AmEur. В Google Spreadsheets поименовать ячейки можно с помощью пункта меню Данные — Настроить именованные диапазоны. Встаем на ячейку, кликаем на пункт и в правой панели Добавить именованный диапазон.
Также введем в ячейки входные параметры — я выбрала опцион call на фьючерс на индекс РТС страйк 185000, ближняя серия (5 дней до экспирации, можно вводить и дробные значения, но для демонстрационных целей мы не будем тут упарываться с долями дней)
Получится так:
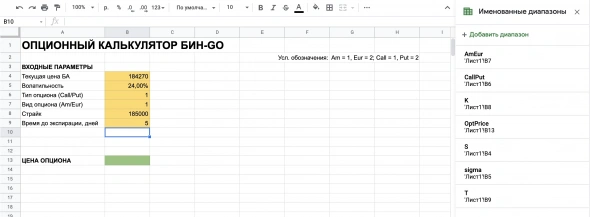
Красота — страшная сила! Подготовка завершена. Едем дальше.
Начнем с того, что построим биномиальное дерево на произвольных фиксированных шагах и произвольных фиксированных вероятностях. Пусть для простоты шаг вверх будет равен шагу вниз и составит 1%, а вероятности движения цены вверх и вниз будут равными — 50/50. У нас пять дней до экспирации, поэтому количество временных отрезков (шагов) будет равно 5, а временной интервал одного шага будет равен одному дню. Дальше, развивая тему, можете сделать свой калькулятор в часах — смысл тот же. Мне на 5 отрезках проще демонстрировать.
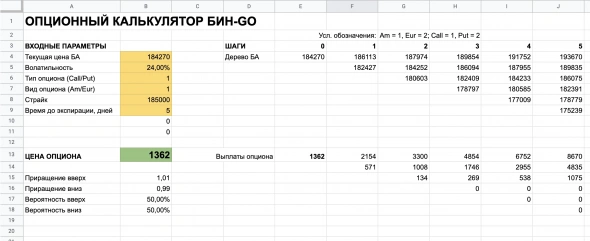
В строке 3 добавим наши 5 шагов, пронумеровав от 0 до 5, где 0 — текущее значение цены БА. В ячейках A15-A18 введем названия шагов и вероятностей, а в ячейках B15-B18 укажем наши выбранные произвольные значения, чтобы получилось вот так:
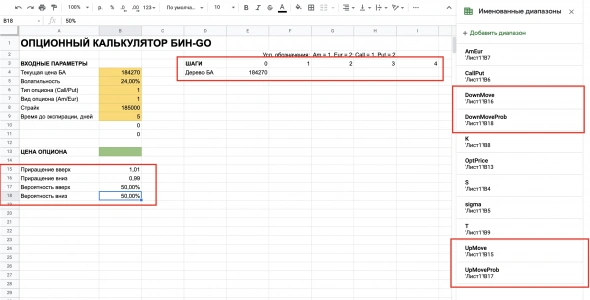
Чтобы получить текущую цену БА в вершине нашего дерева, введем в ячейку E4 формулу =S, где S — как мы помним, имя ячейки с текущей ценой БА.
На бумаге биномиальное дерево выглядит как этакая не обязательно симметричная, но тут симметричная решетка:
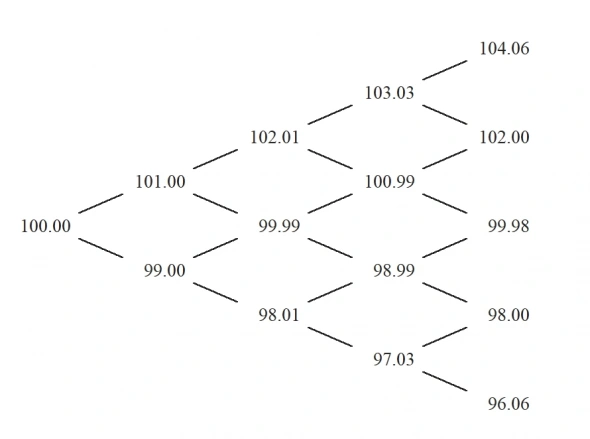
У нас в экселе оно будет выглядеть треугольником, чтобы не морочиться с симметрией и пустыми ячейками. Нулевой узел за шаг не считаем. На шаге 1 у нас станет уже два узла — Текущая цена БА * Приращение вверх и Текущая цена БА * Приращение вниз. В виде формул формулах =E4*UpMove и =E4*DownMove. На шаге 2 у нас будет уже три узла, в формулах =F4*UpMove, =F4 * DownMove, = F5 * DownMove. Продлеваем формулы до пятого шага, где у нас получится 6 итоговых точек-узлов.
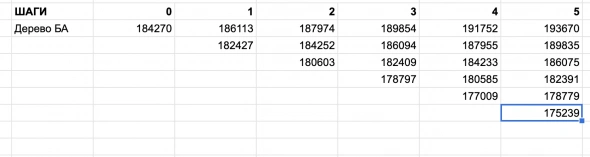
Дерево для БА у нас готово, в последней колонке мы имеем цены на экспирацию. Из них мы посчитаем выплаты нашего целевого 185-го колла на экспирацию. Очевидно, что формула для выплат будет (на примере первой из шести цен на пятом шаге)
Сколько будет стоить опцион в ячейки I13 на шаге 4? Если бы он был европейским, то чтобы найти цену назад, нам нужно уже привлечь вероятности (а они у нас 50 / 50):
Цену опциона рассчитали, поняли, как работает оценка через биномиальные деревья — но выше же было обещано, что размер приращения вверх и вниз, а также вероятности движения вверх и вниз модель посчитает сама из входных параметров! И где?!
Господа, все будет. Даже неоднократно ) В этом расчете состоит различие между разными биномиальными моделями оценки. Пришло время назвать и их: модель Кокса-Росса-Рубинштейна (Cox-Ross-Rubinstein, ничего общего с веществами, это фамилии трех человек) и модель Джарроу-Рудда. Так как мы уже хорошо потрудились, предлагаю оставить их для второй части статьи.
Не переключайте канал! ;)
P.S. Буду признательна за указание на ошибки и неточности.
Суть биномиальной модели оценки в том, что при тех же вводных, что и у Блэка-Шоулза, она строится на разбиении времени до экспирации на равные временные интервалы (отрезки) (а в МБШ время непрерывно), и движение цены от начала одного отрезка к началу другого может быть либо вверх, либо вниз. Модель упрощает реальность ещё и тем, что в процентах шаг движения цены вверх и шаг движения цены вниз на всех отрезках одинаков, при этом шаг вверх может быть не равен шагу вниз. Размер шага вверх и шага вниз рассчитывается моделью из входных данных. Вероятности на следующем отрезке двигаться вверх или вниз также рассчитываются моделью из входных параметров и так же неизменны. Необязательно это будут вероятности 50/50, может получиться любое соотношение в сумме, дающее 100%.
Критикой моделей и их базовых предпосылок мы тут заниматься не будем. Мы тут будем опционный калькулятор писать.
Открываем Google Spreadsheets (MS Excel тоже подойдет, но у меня лапки MacOS, и Excel у меня там не имеется), создаем новый документ. Первый лист его будет представлять «морду» нашего калькулятора и содержать поля для входных параметров и поле для отображения результата расчета. Самое время эти входные параметры перечислить — вот таким образом (ВНИМАНИЕ! номера строк и буквы столбцов будут дальше иметь значение):

Как видите, ничего незнакомого среди входных параметров нет. Волатильность — которая и есть по сути наша ставка, за которую нам платят и с нас берут) — как параметр модели есть, как и в МБШ.
Результат расчета будет выведен в ячейку B13.
Поименуем ячейки, чтобы было проще писать и читать формулы. Я решила остаться в привычной по БШ нотации, где S — текущая цена БА, sigma — волатильность, K — страйк, T — время до экспирации. Для типа опциона буду использовать имя CallPut, для вида опциона (американский или европейский) — AmEur. В Google Spreadsheets поименовать ячейки можно с помощью пункта меню Данные — Настроить именованные диапазоны. Встаем на ячейку, кликаем на пункт и в правой панели Добавить именованный диапазон.
Также введем в ячейки входные параметры — я выбрала опцион call на фьючерс на индекс РТС страйк 185000, ближняя серия (5 дней до экспирации, можно вводить и дробные значения, но для демонстрационных целей мы не будем тут упарываться с долями дней)
Получится так:

Красота — страшная сила! Подготовка завершена. Едем дальше.
Начнем с того, что построим биномиальное дерево на произвольных фиксированных шагах и произвольных фиксированных вероятностях. Пусть для простоты шаг вверх будет равен шагу вниз и составит 1%, а вероятности движения цены вверх и вниз будут равными — 50/50. У нас пять дней до экспирации, поэтому количество временных отрезков (шагов) будет равно 5, а временной интервал одного шага будет равен одному дню. Дальше, развивая тему, можете сделать свой калькулятор в часах — смысл тот же. Мне на 5 отрезках проще демонстрировать.
В строке 3 добавим наши 5 шагов, пронумеровав от 0 до 5, где 0 — текущее значение цены БА. В ячейках A15-A18 введем названия шагов и вероятностей, а в ячейках B15-B18 укажем наши выбранные произвольные значения, чтобы получилось вот так:

Чтобы получить текущую цену БА в вершине нашего дерева, введем в ячейку E4 формулу =S, где S — как мы помним, имя ячейки с текущей ценой БА.
На бумаге биномиальное дерево выглядит как этакая не обязательно симметричная, но тут симметричная решетка:

У нас в экселе оно будет выглядеть треугольником, чтобы не морочиться с симметрией и пустыми ячейками. Нулевой узел за шаг не считаем. На шаге 1 у нас станет уже два узла — Текущая цена БА * Приращение вверх и Текущая цена БА * Приращение вниз. В виде формул формулах =E4*UpMove и =E4*DownMove. На шаге 2 у нас будет уже три узла, в формулах =F4*UpMove, =F4 * DownMove, = F5 * DownMove. Продлеваем формулы до пятого шага, где у нас получится 6 итоговых точек-узлов.

Дерево для БА у нас готово, в последней колонке мы имеем цены на экспирацию. Из них мы посчитаем выплаты нашего целевого 185-го колла на экспирацию. Очевидно, что формула для выплат будет (на примере первой из шести цен на пятом шаге)
=MAX(0;IF(CallPut=1;J4-K;K-J4))Растягиваем формулу вниз на 6 строк, получаем выплаты на экспирацию по 185-му коллу в каждой точке. Итак имеем на пятом шаге 6 цен выплат, и теперь нам предстоит построить дерево для опционов с конца в начало.
Сколько будет стоить опцион в ячейки I13 на шаге 4? Если бы он был европейским, то чтобы найти цену назад, нам нужно уже привлечь вероятности (а они у нас 50 / 50):
=(J13*UpMoveProb+J14*DownMoveProb)Но наш опцион американский, а это значит, что он может экспирироваться в любой момент, значит, нужно учесть еще и это. И тогда формула получится для предыдущей цены:
=MAX((J13*UpMoveProb+J14*DownMoveProb);IF(AmEur=1;IF(CallPut=1;I4-K;K-I4);0))Растягиваем формулу, достраивая дерево назад, соблюдая количество узлов на каждом шаге. В ячейке E13 мы получим текущую цену опциона, значит в ячейке B13 у нас будет формула =E13

Цену опциона рассчитали, поняли, как работает оценка через биномиальные деревья — но выше же было обещано, что размер приращения вверх и вниз, а также вероятности движения вверх и вниз модель посчитает сама из входных параметров! И где?!
Господа, все будет. Даже неоднократно ) В этом расчете состоит различие между разными биномиальными моделями оценки. Пришло время назвать и их: модель Кокса-Росса-Рубинштейна (Cox-Ross-Rubinstein, ничего общего с веществами, это фамилии трех человек) и модель Джарроу-Рудда. Так как мы уже хорошо потрудились, предлагаю оставить их для второй части статьи.
Не переключайте канал! ;)
P.S. Буду признательна за указание на ошибки и неточности.
2.2К |
Читайте на SMART-LAB:

Тамбовэнергосбыт и Саратовэнерго. Отчет РСБУ. Сколько заработали дочки Интер РАО за 25г.?
Компания Тамбовэнергосбыт (сокр. ТЭСК) опубликовала финансовый отчет за Q4 и за весь 2025г. по РСБУ: 👉Прибыль от продаж — 0,110 млрд...
15:58

Реконцепция ТЦ «Сокольники»: через тернии к звёздам
«Если важный проект выпадает на сложные времена, он становится великим», — кто-то из классиков 😉 Проект реконцепции ТЦ «Сокольники» застал...
17:50
теги блога tashik
- google таблицы
- hedge
- HV
- OptionVictory
- PineScript
- python
- tradingveiw
- Tradingview
- алготрейдинг
- биномиальная модель
- БОТ
- введение
- волаильность
- волатильность
- Греки
- дельта-хеджирование
- дельтахеджирование
- дельтахэдж
- иГРЫрАЗУМа 2019
- иГРЫрАЗУМа-2019
- иксы
- индикатор
- итоги 2021
- итоги 2022
- итоги года
- Кирилл Ильинский
- книги
- конкурс
- конспект
- лотерея
- лчи
- направленная торговля опционами
- опционы
- Опционы RI
- открытый интерес
- отчет за месяц
- оффтоп
- пари
- покупка волатильности
- продажа волатильности
- робот
- руководство
- Скальпинг
- стандартное отклонение
- статисика
- стратегия
- тест
- толстые хвосты
- торговая система
- торговля волатильностью
- торговые роботы
- торговый робот
- торговый софт
- трейдинг
- управление опционной позицией
- управление позицией
- управление рисками
- финансовое моделирование
- фьючерсы
- хэджирование
- эпик фейл
- юмор




















Спасибо, так и должны выглядеть посты на смартлабе.
Без мути, и махания всем, чем попало в виде эквити :)
Где брать данные для дерева?
Где простой протокол ввода данных?
Где лично Вы видели подряд хотя бы пять свечек одинакового размера???
В этой части мы на умозрительных произвольных входных приращениях и вероятностях научились строить дерево и поняли логику того, что делается биномиальными моделями: два дерева — от текущей цены до экспирации на фьючерсе, а потом назад от экспирации к цене опциона в текущей точке.
Во второй части — и в конце статьи про это упомянуто, мы реализуем расчет самого интересного — приращения вверх и вниз и вероятностей движения вверх и вниз по разным биномиальным моделям.
Найдете ли лично Вы в этом практическое зерно и какое — не знаю, может и никакого не найдете.
Давайте сделаем так:
— у меня сейчас нет доступа к моим it-наработкам;
— в течении месяца я их сформулирую письменно, и отправлю Вам в личку;
— в ответ буду ждать конструктивной критики моих результатов, может быть даже исправлений и некоторых допущений:))
Ничего там не будет нового. При достаточно малом шаге все сойдется к МБШ один в один, хоть равный шаг вверх и вниз, и вероятности, хоть нет. Потому что существует Центральная Предельная Теорема, согласно которой сумма любых независимых отклонений в конечном счете — Гаусс.
То есть модель не даст вам абсолютно ничего, разве что учет «отрицательных цен», если будет работать не в логарифмическом, а в натуральном масштабе. Но вы и МБШ можете в натуральном прогнать при желании.
Иными словами, конкретно в дереве «фишек» нет, но они могут быть побочным продуктом выбора другой системы предобработки данных.
Хотя это все конечно же частности.
Например как в соседней ветке — игроки во фьючах яндекса не принимают решения чаще чем раз в 5 минут — там ЦПТ работает (работает конечно нооо )?