Блог им. noHurry
Откуда берется улыбка волатильности.
- 10 ноября 2019, 14:53
- |
Вот эта картинка очень просто обьясняет, почему рынок имеет или должен иметь улыбку.
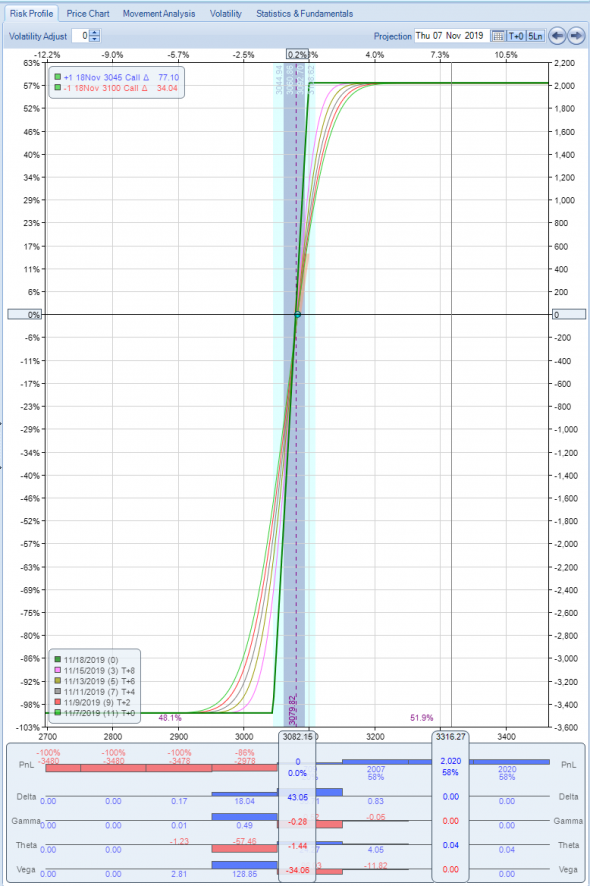
Это простой вертикальный Bull call spread на SPX, с нулевой теттой. Обратите внимание на соотношение max P/max L. Я думаю любой более менее понимающий этот рынок скажет, что так и должно быть, иначе деньги можно было бы лопатой грести. А теперь вопрос — а возможно ли было бы такое без улыбки? Мой ответ нет. Чем отличается рынок SPX от других рынков, где нет улыбки, тем, что он трендовый.
Вывод — причина возникновения улыбки волатильности это трендовость рынка.
Рынок саморегулирующийся механизм, который стремится к нулевому матожиданию. И если у рынка появляется трендовость (смещение вероятности), то рынок компенсирует это смещением волатильности и возвращает матожидание к нулю.























У стационарного ряда % приращений цен даже с «тяжёлыми хвостами» одномерного распределения «улыбки» быть не должно.
Кусочная стационарность это стационарность на интервале времени >0.
Автокорреляционная стационарность это стационарность процесса на интервале времени = 0; Это разные вещи.
Итого тренд (кусочный) — равномерно размазанная по лагам АКФ.
Итого персистентность — положительная АКФ ближних лагов.
Вот, например, коррелограмма реального процесса приращений кусочно-стационарного 5% тренда на российских акциях.
*Ссылки ещё не смотрел.
«Рынок саморегулирующийся механизм, который стремится к нулевому матожиданию. И если у рынка появляется трендовость (смещение вероятности), то рынок компенсирует это смещением волатильности и возвращает матожидание к нулю. „
Это безусловно так, но у этого процесса есть характерные времена. И они немаленькие. Рынку надо понять, что перед ним--с систематическим смещением или без него. Условно, есть инструменты, в которых “считается» что они всегда растут (или всегда падают)--индексы, еще что-то. В них ценообразование опционов одно, такое как вы описали--финрез ба+опционы равен нулю. А есть инструменты (акции отдельные например как правило), в которых «считается» что они без тренда или с малым трендом--в них ценообразование такое, что финрез опционов (без ба) равен нулю. А бывают промежуточные.
Ну и улыбка это не только скос. Там еще вогнутость есть. То есть утверждение о том, что трендовость есть причина возникновения улыбки--ну оно сильное слишком имхо. Улыбки (то есть зависимость iv(strike) не равна константе) есть почти везде, даже в том, что уж точно на систематический тренд не похоже.
Есть тут тренд? Ну не очевидно как минимум. А вот кривая волатильности:
Тут явный скос.
А вот акция GE со ставшим уже классическим многолетним трендом вниз:
А вот ее улыбка, скошенная в ту же сторону, что и «вечнорастущая» тесла.
А по вашей теории скос должен быть в другую сторону. Кароч, случаи бывают разные, и улыбка--это не следствие тренда. Коррелирована безусловно--но не напрямую и не следствие.