SMART-LAB
Новый дизайн
Мы делаем деньги на бирже
Блог им. bstone
Теория управления... счетом?
- 17 февраля 2019, 01:21
- |
Тут недавно помянули теорию оптимального управления. Жаль без конкретики. Зато Дмитрий Новиков недавно даже пытался протолкнуть идею об управлении эквити как опционной позицией. Там и свихнуться не долго, но тема по-своему интересная.
А я предлагаю взглянуть на это по-взрослому. Спрячем оптимальность под ковер, тут и без нее есть над чем подумать. Итак один из простейших видов систем управления — следящая система:
y(t) = F[ x(t), g(t), u(t) ]
где y(t) — сигнал на выходе системы, x(t) — вектор состояния системы, g(t) — уставка, u(t) — управляющее воздействие
Задача системы — повторять задающее воздействие g(t).
Ну что? Сразу ведь понятно, как это применить в трейдинге? Я так и подумал! Поэтому мы с вами тотчас приступим к делу:
1) За y(t) возьмем баланс нашего любимого (как и полагается, многомиллионного и секретного) счета.
2) За единственную наблюдаемую переменную состояния системы x(t) возьмем стоимость Ришки
3) Задающее воздействие? Элементарно — хочу, чтобы счет постоянно рос на 100 пунктов в час.
4) Закон управления? Это самое интересное, но цель поста — воспалить сознание читателей. Мне нужны ваши эмоции и мысли, поэтому я не засоряю ваше сознание конкретикой (но на графике все видно :)). Так победим!
Уравнение системы (для наглядности время t будем измерять в часах, см. п. 3 выше):
dy/dt = u(t) * dx/dt
g(t) = 100 * t
Что оно описывает? Да это ж дифференциальное уравнения лудоманства в чистом виде! А именно: скорость изменения баланса нашего счета пропорциональна изменению цены Ришки с коэффициентом u(t).
Т.е. мы подключаем наш счет к рынку с коэффициентом усиления u(t). Это кстати очень глубокая мысль. Дарю.
А вот как это выглядит в понятном любому обитателю смартлаба виде:
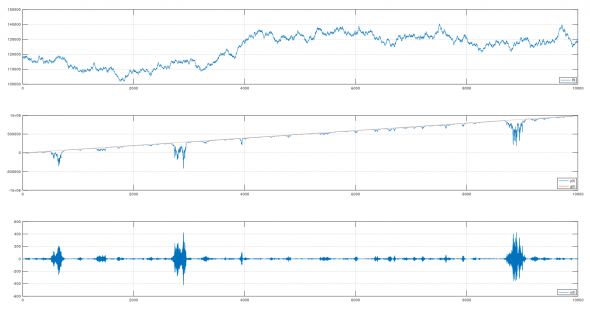
Вверху — можно считать часовой график RI, смоделированный с волатильностью 23% (специалисты тут могут потренироваться в волновой разметке и в обнаружении трендов).
Посередине — наш красавец счет (в пунктах). Как видите — система управляет им как ей велено — счет растет с заданной скоростью. Автоматика-телемеханика и никакой уличной магии.
Внизу — наше управляющее воздействие, т.е. рыночная позиция в контрактах.
Ну как? Предвидя некоторую критику по поводу просадки, я все-таки на всякий случай озвучу, что вы видите на картинке: на входе абсолютно случайное движение цены, а система управления преобразует его в рост вашего депозита с заданной скоростью. Лично я всегда думал, что это очень круто, но это конечно не миллионы за час-другой на тусовке трейдеров-чемпионов (которые, к слову, допускают просадки и покруче) :)
Пробуйте и делитесь результатами. Здесь не паханное поле для исследований. Думаю будет интересно.
А я предлагаю взглянуть на это по-взрослому. Спрячем оптимальность под ковер, тут и без нее есть над чем подумать. Итак один из простейших видов систем управления — следящая система:
y(t) = F[ x(t), g(t), u(t) ]
где y(t) — сигнал на выходе системы, x(t) — вектор состояния системы, g(t) — уставка, u(t) — управляющее воздействие
Задача системы — повторять задающее воздействие g(t).
Ну что? Сразу ведь понятно, как это применить в трейдинге? Я так и подумал! Поэтому мы с вами тотчас приступим к делу:
1) За y(t) возьмем баланс нашего любимого (как и полагается, многомиллионного и секретного) счета.
2) За единственную наблюдаемую переменную состояния системы x(t) возьмем стоимость Ришки
3) Задающее воздействие? Элементарно — хочу, чтобы счет постоянно рос на 100 пунктов в час.
4) Закон управления? Это самое интересное, но цель поста — воспалить сознание читателей. Мне нужны ваши эмоции и мысли, поэтому я не засоряю ваше сознание конкретикой (но на графике все видно :)). Так победим!
Уравнение системы (для наглядности время t будем измерять в часах, см. п. 3 выше):
dy/dt = u(t) * dx/dt
g(t) = 100 * t
Что оно описывает? Да это ж дифференциальное уравнения лудоманства в чистом виде! А именно: скорость изменения баланса нашего счета пропорциональна изменению цены Ришки с коэффициентом u(t).
Т.е. мы подключаем наш счет к рынку с коэффициентом усиления u(t). Это кстати очень глубокая мысль. Дарю.
А вот как это выглядит в понятном любому обитателю смартлаба виде:

Вверху — можно считать часовой график RI, смоделированный с волатильностью 23% (специалисты тут могут потренироваться в волновой разметке и в обнаружении трендов).
Посередине — наш красавец счет (в пунктах). Как видите — система управляет им как ей велено — счет растет с заданной скоростью. Автоматика-телемеханика и никакой уличной магии.
Внизу — наше управляющее воздействие, т.е. рыночная позиция в контрактах.
Ну как? Предвидя некоторую критику по поводу просадки, я все-таки на всякий случай озвучу, что вы видите на картинке: на входе абсолютно случайное движение цены, а система управления преобразует его в рост вашего депозита с заданной скоростью. Лично я всегда думал, что это очень круто, но это конечно не миллионы за час-другой на тусовке трейдеров-чемпионов (которые, к слову, допускают просадки и покруче) :)
Пробуйте и делитесь результатами. Здесь не паханное поле для исследований. Думаю будет интересно.
5.5К |
Читайте на SMART-LAB:

BRENT: Война или сделка? Как ликвидация аятоллы изменит цену «черного золота»
«Черное золото» в эти выходные стало эпицентром глобального шторма. Совместная операция США и Израиля привела к ликвидации высшего руководства...
22:56

Мой Рюкзак #64: Усиление в банковском секторе в ожидании справедливой переоценки
Февраль продолжает радовать стоимостных и смелых инвесторов
Прошлый пост тут — smart-lab.ru/company/mozgovik/blog/1265828.php...
01:16
теги блога bstone
- Intraday
- LUA
- Ri
- SR
- Аллирог
- аналитик
- аналитика
- биржа
- Блэк-Шоулз
- бонус
- брокеры
- вероятность
- визуализация сделок
- Волантильность
- волатильность
- волны эллиота
- Волотильность
- герчик
- демо форекс
- депо
- депозит
- Дискреционный трейдинг
- ДУ
- интрадей
- книга
- Книги
- Коровин
- короткий стоп
- кризис
- кукл
- лчи
- лчи 2015
- Маркидон
- мобильный пост
- Нефть
- опрос
- опцион
- опционы
- опыт
- открытие брокер
- оффтоп
- просадка
- психология трейдинга
- развод
- рецензии
- рецензия
- риск
- роботы
- рублебакс
- рынок
- Сбер
- сбербанк
- Сбой на бирже
- сделки
- семинар Герчика
- си
- скальп
- слив
- смартлаб
- стакан
- стоп
- Стоп-лосс
- ТА
- технический анализ
- торговые роботы
- трейдер
- трейдинг
- улыбка волатильности
- уровни
- шорты
- Эллиот
- юмор




















Я Вам ответил в своем топике — задача решена, всем откликнувшимся — респект и уважуха.
Что касается применения теории управления к рыночным (и не очень) процессам — могу рассказать пару историй из жизни. Если вкратце — без модели того, что происходит внутри черного ящика, шансов практически нет.
Будет любопытно — маякните — отпишусь.
Жизненные истории — это всегда интересно. Жизненные истории по применению теории управления к любым процессам — это втройне интересно. Буду рад почитать, однозначно.
В далеком-далеком 1990 году заказчик прислал нам задачу.
Да-да, и в те времена научное сообщество не могло игнорировать поток мысли из реального сектора, в данном случае — ВПК.
Речь шла о решении задачи управления асинхронным электродвигателем (в Гугле — задача Сименса, ну или Siemens challenge). История вполне себе с бородой, если че
Теперь по делу — задача представляет из себя систему дифуров 3-го порядка. При этом в правой части — полная трансцедентность. Синусы там, косинусы, ну и прочая ересь.
Поскольку задача оказалась суперактуальной (на решение было отведено 30 дней, да и заказчик был не лыком деланый) — универ оперативно сформировал рабочую группу, в которую попал Ваш покорный слуга. Как мальчик из другой специальности, но все же способный. Всем нам обещали золотые горы, в итоге нихуа не дали, ессно.
Мне, к моему огромному удивлению, удалось побороть эту проблему за 2 недели. Я, как алгебраист, придумал преобразование системы координат, после применения которого дифуры превратились в те же 3 штуки, но с полиномиальной правой частью.
В этой правой части были линейные и кубические члены. Последние оказались критически важными для нахождения оптимальной модели управления.
К чему я все это рассказываю? Пока длился challenge — я оставался темной лошадкой — на мою победу никто не ставил. И все эти долгие 2 недели я выслушивал от наших «грандов», что в теории управления работают только линейные и квадратичные компоненты, все остальное — некошерно.
После публикации результата меня встретило глухое молчание в зале. Засим высказался старший в духе «Ну да. Природа не отрицает исключения».
Это — фсе. Дописал до этого момента я ровно по одной причине. В прошлом году глубокоуважаемый мною лично А.Г. мотивированно пояснил, почему в методиках анализа и прогноза случайных процессов, связанных с ценообразованием рыночных активов, не стоит заморачиваться с моделями, включающими нелинейности более, чем второй степени, в части приращений цены актива.
А я именно их и использую ((( И кто я после этого?(
Позиция А.Г. вполне объяснима. Но тут важно понимать, что вклад степеней приращений цены зависит от модели. Там где третья степень входит как O(t^3) я и сам ее выкину без тени сомнения. И это просто самый распространенный случай в финансовой математике. А если в вашей модели вклад кубических приращений существенный, то и использовать их не грех, как по мне.
Будут нужны еще истории по жизни с оптимальным управлением — сигнальте. Их есть у меня )))
P.S. Третья степень в самой задаче редко приводит к O(t^3) на выходе. Я и более старшие компоненты легко отправляю в мусор.
У Вас просто подход не стандартный, скорее всего. Общепринятым является разложения в ряд Тейлора с последующим применением леммы Ито. И там выкидывают все от О(t^2) и хуже, что в итоге оставляет только квадратичные приращения цены. Но это не задачи управления — своя специфика.
Кстати, а опционами вы, случайно, не барыжите?
А то мои падаваны любят как раз с опционов начинать…
Опционами барыжу потихоньку, но пока исключительно покупаю от центрального страйка — мне так комфортно получать большое плечо (и не пялиться в экран 24 часа в сутки).
А так для меня опцион — это машина, в которой кроме руля, газа и тормоза есть еще штук 20 кнопок, как у Шумахера в Феррари, и все, сцуко, важные. Это сложно — нам бы для начала обычную научиться хорошо пилотировать.
С уважением
Да я и без этого… А еще я крестиком вышивать умею...
А если серьезно — решения не было, конечно. Просто полиномиальная правая часть сильно упрощает учет дополнительного члена в виде управляющего воздействия.
Просто в нашей рабочей группе (см. многобукофф выше) были и компьютерные энтузиасты, которые пытались подобрать субоптимальное управление методом научного тыка и последующего моделирования.
Так вот, когда я им показал график (ну и формулу ессно) оптимального управления, оказалось, что никто даже близко не пытался тестировать такие управляющие функции.
Поэтому сначала модель — потом уже оценка шансов прибыли.
За гарантиями — в страховую компанию плз.
Если бы у меня была сколь-нибудь исчерпывающая модель функционирования рынка — я бы заходил на этот форум исключительно в пьяном виде поболтать за баб…
Мальчик Buybuy, а как понять, являются ли рассматриваемые модели рынка «более-менее исчерпывающими»?
Есть ли чёткие признаки этого?
Как по мне — в теории должен содержаться некий материал для построения гипотез и их проверки. Типа, предсказания.
Хотя в жизни все сложнее. ОТО Эйнштейна долго болталась, как сферический конь в вакууме, до первых подтверждений. С термодинамикой похожая хня была, хотя она значительно старше.
Каждый третий сигнальщик постиг этот метод.
Размер средств на счете:
Загрузка счета (объем позиций), т.е. управляющее воздействие:
пост интересный. но за что недолюбливаю математиков, они заставляют всех следовать их собственному птичьему языку, вместо того чтобы хоть немного постараться объяснить главный вывод обычными словами.
ведь что такое математика: перевод на язык символов некоей модели реальности и манипуляция этой моделью с помощью языков символов.
почему математики считают что объяснять обратное преобразование, из языка символов в реальный смысл — это западло?
пытаюсь применить свои знания,
получается что управляющее воздействие (изменение размера позы?)
обратно пропорционально изменению цены Ри (dx) и прямо пропорционально волатильности счёта (dy) .
u(t) = dy/dx
т.е.
Ри вниз (dx<0), счёт растёт (dy>0) — размер позы уменьшаем
Ри вверх (dx>0), счёт растет (dy>0) — размер позы увеличиваем
но
если Ри падает и счёт падает, уменьшаем позу
если Ри растёт и счёт падает, то уменьшаем позу
так?
Далее, не управляющее воздействие пропорционально изменению цены. Оно может быть любым — это вы управляете счетом. Например вы можете сделать u(t) = 0 и ваш счет просто радует брокера и не зависит от рынка. Или сделайте u(t) = 1 и у вас получится система-долгосрочный инвестор :)
А вот изменение баланса счета у вас будет пропорционально изменению цены и вашему управлению, т.е. dy/dt = u(t) * dx/dt
У рассмотренной системы есть задача — повторять уставку, т.е. задающий сигнал g(t). Если она не справляется, то возникает рассогласование/ошибка:
e(t) = g(t) — y(t)
Поэтому в простейшем случае вы можете управлять системой вот так, например:
u(t) = k * e(t)
Т.е. ваша позиция пропорциональна рассогласованию с желаемым результатом. Это простейший, пропорциональный регулятор. Классикой теории систем являются пропорционально-интегрально-дифференциальные (ПИД) регуляторы, которые могут учитывать скорость изменения ошибки, входа, выхода, переменных состояния (дифференциал), а также накапливаемую ошибку и т.п. (интеграл). Это можно почитать в википедии.
Как-то так.
спасибо за терпеливое объяснение
1) u(t) = k * e(t)
2) u(t) = -k * e(t)
То сравнение результатов может пошатать вам трубу :)
Но как я уже отметил, это простейший случай. ПИД регуляторы уже не похожи на мартин, особенно если обнулить в них П. И я уже не говорю об оптимальном управлении или просто нелинейном управлении в общем случае.
интересны те, которые позволяют не пилиться в боковиках и быстро вгружаться без всякого остатка в тренды.
тут с точки зрения и программирования есть над чем попыхтеть, т.е. эта модель описанная здесь, не даёт ответа на вопросы, где входить и сколькими частями и как.
dy/dt = u(t) * dx/dt + h(t)
где h(t) — сумма пополнения/снятия в момент времени t.
Как мы делаем сделку. Выбрали вход, поставили цель, поставили стоп. В этом месте мы можем ошибаться. И ошибаться с точностью до Гауса. То есть цена пошла к нашей цели, но не дошла за определенное нами время. Это значит что есть вероятность или ошибка что она туда не дойдет. Тогда вверх у нас N(d1). У нас 100 баксов капитала. Тогда 100*N(d1)-100*N(d2). Ну и дальше по смыслу…
А так наскок зачётный.
Вот формула из вики.
А по поводу методов обхода неоднозначностей, надо исследовать их, насколько выдаваемое через них псевдорешение удовлетворительно. А эта задача ничуть не проще исходной.
А чисто по прухе — и в казино пацаны нарядные серии показывают.
Как любят говаривать евреи — если бы турник был полезен для здоровья — на каждом бы висело минимум шесть евреев )))
Но и в простые решения не верю. PC cтали доступны с 1982, в России — с 1992. Все, что можно посчитать, было посчитано. Где Грааль?
С уважением
А так — чем подтверждать? Новостями? Объемами? Другими индикаторами? Суета все это
Если вкратце — я не верю в паттерны без четких формул. Человеческий глаз плохо приспособлен для анализа графиков цен рыночных активов.
К примеру (по Эллиотту) движение индекса ММВБ с 2008-09 по настоящее время — это импульс, а индекса РТС — коррекция. Теперь смотрим на графики и пытаемся найти 10 отличий…
Но придется угадывать (см. мой пост выше про креативных программеров)
Инструментарий для экспериментов сейчас фантастический — это не только Эксел, как в 90-е, или миллиметровка в 60-е.
Риск-менеджмент вторичен IMHO без наличия стратегии с положительным матожиданием. Просто помогает медленнее разориться.
Причем детально оттестированная
Все формулы для управления риском, хошь по Келли, хошь по Винсу, явным образом зависят от процента прибыльных сделок и их среднего результата.
Дисперсия в отдельности вообще не при чем, параметры кривой Эквити определяет МО/Д, ну или МО/СКО (кому как удобнее считать).
Но без положительного МО все это не имеет никакого смысла.
Давайте тогда уж применим Винса к рулетке?
Келли не получится — f будет отрицательное.
Поэтому давайте не будем особо придираться
МО — угол наклона Эквити. МО/Д — мера просадки
Но, Холмс, ради бога, Холмс, как можно строить РМ только на основании дисперсии?
Если для РМ МО не нужно — как должен выглядеть РМ для игры с отрицательным МО? (рулетка, к примеру) И почему?
С уважением
Как можно заметить в любой ТС есть отрицательные сделки и есть положительные. Тогда (без дифуров, что бы все поняли) у вас наблюдается дисперисия ваших результатов. сигма^2*Т. Разброс относительно средней за время Т. Давайте рассмотрим этот разброс в обе стороны. В верх D=1/2 сигма^2*Т (положительный результат) и D вниз= -1/2 сигма^2*Т. То есть D это половину сигмы в квадрате. Давайте переведем наше D в привычную нам волатильность. Разделим левую и правую часть на сигма* Т^0.5 и назовем это d1 вверх и d2 вниз. Получим d1=(1/2*sig^2*T)/sig*T^0.5, а d2=d1-sig*Т^0.5. То есть d1 это наши положительные сделки за время Т, а d2 отрицательные сделки за то же время.
Как мы делаем сделку. Выбрали вход, поставили цель, поставили стоп. В этом месте мы можем ошибаться. И ошибаться с точностью до Гауса. То есть цена пошла к нашей цели, но не дошла за определенное нами время. Это значит что есть вероятность или ошибка что она туда не дойдет. Тогда вверх у нас N(d1). У нас 100 баксов капитала. Тогда 100*N(d1)-100*N(d2). Ну и дальше по смыслу…
Далее вам надо увеличивать вложения по ходу роста вашего депо и уменьшать по ходу падения. Или увеличивать по ходу падения… Согласно N(d1).
Внимательно прочитал. Ну да, грамотная работа в коридоре. А если МО отрицательное и коридор смотрит вниз — вся конструкция разваливается, не?
То что коридор смотрит вниз должно быть не визуально. Должно быть сигма*сигма*сигма=(-). Тогда увеличение вложений при падающем экви должно быть реже или меньше. (эффект улыбки волатильности).
Бывают акции с хорошими дивами по падающие. Вот по этой схеме их и можно торговать.
Вот есть европейская рулетка (с одним зеро). МО=-1/37. Опционов нет.
Как строим РМ?
Как и при любом другом попадании в цифру.
Зря Вы все время на опционы переходите, IMHO. Это как машина с 100500 педалей разных. Круто, конечно, но как водить — непонятно.
От самого МО трудно уйти даже такими изящными рассуждениями, которыми Вы оперируете.
Если МО положительно — Эквити будет болтаться вокруг прямой (ну или экспоненты) с коэффициентом наклона = МО. А МО/Д будет параметром расширяющегося коридора, построенного вокруг этой прямой. При этом кривая Эквити с вероятностью 100% попадет внутрь этого коридора.
Если угол наклона прямой невелик, а дисперсия высока, в начале времен будет период, когда Эквити может зайти в минус при положительном МО. Длина этого периода будет зависеть как от МО, так и от МО/Д.
И т.д., и т.п.
Это формула дифференциала цены. Трэба проинтегрировать.
А так — МО то, что рядом с dt стоит. И цена будет расти с увеличением t.
В реалии мы опять говорим на разных языках. МО — это характеристика торговой стратегии, а не цены актива.
В МЮ входят дивиденды, проценты, и все то что постоянно. Поэтому туда не сигму ни сигму ни броуна не подставить.
Относительно ТС. Можно определить положительность ТС как дрифт. Тогда мы говорим, что при любом раскладе мы должны получить 5%. Тогда, при расчетах, мы не смотрим на эти 5% а считаем дисперсию. Наш фин рез=5%+что то там болтается.
Тут конечно трудно разделить понятия. Но если мы говорим про МО, то получается, что это финансовый результат, минус курсовая разница.
По логике, доха и риск должны быть в одинаковых единицах, в рублях или в %. Или не так?
Хотите корректную нормировку — делите МО на СКО
Но в формулах все равно МО/Д появится )))
Безразмерные они на самом деле. Просто представьте, что в далеком прошлом евро стоило 1 доллар… Ну или бочка нефти стоила 1 доллар…
Откуда, кстати дисперсия появляется, не понял. В Шарпе СКО.
Попробуйте посчитать коридор отклонения Эквити от прямой с коэффициентом наклона = МО. У меня вылезает МО/Д (вроде, давно не пересчитывал)
Шарп — это к экономистам
Чисто экспериментально?
Мы с Вами на разных языках разговариваем.
Пусть на каждом шаге мы имеем испытание Бернулли. Результат +X c вероятностью P и -Y с вероятностью Q. МО и Д считаются легко.
Если МО>0 — счет растет, ессно. Мерой просадки является именно МО/Д. Грубо — параметр расширяющегося коридора, внутри которого с вероятностью 100% умещается кривая Эквити.
Просадки могут быть очень глубокими даже при положительном МО.
В топике про математику казино я писал, что при оптимальной для игры стратегии с положительным МО можно легко проиграть 100 ставок по Келли (грубо 2 депозита при риске 2% на сделку). Можно и больше, но реже.
Это не значит, что убытки будут идти непрерывной чередой, но бывают долгие и страшные последовательности лоссов.
С уважением
P.S. Вероятность полного разорения при ставке по Келли — 5% вроде.
Считать ДД нарастающим итогом — это то же самое, что использовать для его расчета некую линейную статистику (в классическом смысле этого слова).
Чтобы она хорошо работала (не сбоила) — требуется, чтобы сам процесс удовлетворял неким условиям. А что мы знаем про ценовые процессы? Да вообще ничего, кроме их явной нестационарности.
Выборочная оценка — это тоже внешняя статистика.
Я пытаюсь оценивать процесс, исходя из уже разработанной модели. Потом сравнивать с реальностью. В случае расхождения — думать, что могло пойти не так.
Если с самого начала оценивать все постфактум — непонятно, что же предпринимать в случае сбоя.
Что касаестся обнаружения разладки между прошлыми эмпирическими оценками и новыми данными… опять непонятно, как лучше это делать. По макс.ДД, по отклонению от модели, по критерию однородности выборок. Я не знаю.
Если не использовать плечи, добавляться или реинвестироваться.
Если цена — это случайное блуждание (винеровский процесс, в чем лично я глубоко сомневаюсь) — то такое же, как у суммы логнормальных распределений с подобранными конкретно для Сбера МО и дисперсией.
А в чем вопрос то? Смысла особого в нем нет. Если это под"№; ка — давайте вместе посмеемся )))
В среднем за много лет — около 0,5 минус расходы. Т. е. < 0.5.
На растущем тренде >0.5. Если горизонт не слишком далёкий.
За пару месяцев до дивидендов >0.5.
На падающем тренде < 0.5.
Зато можно получить плечо 1:50 — 1:100 без геморроя, постоянных довносов ГО и упирания носом в монитор.
Если уверен в стороне сделки, ессно
Общеизвестных правил полно, но все они неправильные. Потому что модель в их основе неправильно описывает график.
«Если я вижу, что в этой ситуации в 60% случаев на протяжении долгого времени происходит то-то, то я должен понять ПОЧЕМУ».
Или наоборот, долго происходило, а теперь перестало. ПОЧЕМУ?
В качестве конкретики. Всем известные «уровни». Когда до какого-то остаётся 0,25%, то в 80+% случаев до него цена добивает. На этом копеечку можно брать постоянно.
Моё объяснение, что пара-тройка маркет-мейкеров сговариваются совместными усилиями, или усилиями одного из них, уровень достичь.
На спокойном рынке им никто не возразит более крупными объёмами в другую сторону.
у меня проще задача:
1.положительное МО
2.управление капиталом.
но я и не математик…
1. Монотонный рост по 100 пунктов в час
2. Попеременные рост-падение по 100 пунктов
3. Монотонное падение
До кучи синус на вход можно подсунуть с амплитудой 150 пунктов к примеру
1) монотонный рост по 100п/час:
2) монотонное падение:
3) болтанка 100п/ч:
4) синус 150п:
Как видите, система никогда не достигает цели и работает со статической ошибкой.