SMART-LAB
Новый дизайн
Мы делаем деньги на бирже
Блог им. neophyte
Игры разума с ММ - 1. Игра с нулевой суммой. Идеальная монетка.
- 27 октября 2015, 13:49
- |
Среднестатистический трейдер склонен недооценивать важность управления рисками в своей торговой практике. По мнению большинства экспертов, а также по моему мнению и личному опыту, это главная (правда не единственная) причина неудач в торговой практике, особенно со скоропостижным летальным итогом для торгового счета.

Чтобы излагаемый материал был более наглядным я сконструировал небольшой симулятор игр (на экселе), который показывает ожидаемый результат серии ставок (сделок) с заданной статистикой.
Сразу замечу, что в торговле все намного сложнее, потому что в отличие от классической игры с заранее заданным набором исходов торговая практика намного богаче.
Если в игре ставка это проигрыш и он заранее известен, а также известен выигрыш при благоприятном исходе, то в торговой практике все выглядит немного по другому.
Даже если вы заранее задали размер риска на сделку, и даже если размер риска у вас нормирован для всех сделок с любыми инструментами (это возможно и это единственно правильный подход при грамотном ММ), все равно набор исходов ставки (сделки) намного богаче:
— позиция закрыта ордером тейк-профит (этот вариант можно отнести к исходу с выигрышем в классической игре);
— позиция закрыта ордером стоп-лосс (этот вариант можно отнести к исходу с проигрышем в классической игре);
— позиция закрыта по рынку с прибылью меньшей, чем тейк-профит;
— позиция закрыта по рынку с убытком, меньшим, чем стоп-лосс.
Два последних случая портят красивую картинку, но начнем мы с классической теории игр и первой у нас будет игра с нулевой суммой — идеальная монетка без ребра, вероятность выпадения орла и решки одинакова. Выигрывает либо тот либо тот вариант. Комиссия (доля казино или иного заведения) равна нулю.
В дальнейшем у нас будет использоваться следующая система обозначений:
К — капитал, стартовая сумма игры.
L — размер ставки, потери при проигрыше.
R=W/L — отношение выигрыша к проигрышу.
P — вероятность благоприятного исхода.
f=(P(R+1)-1)/RL — формула Келли, связывающая размер оптимальной ставки с условиями игры (огромное спасибо ПBМ за указанную ошибку в формуле).
Если известно f, то
Lopt=f*K.
Знакомо, не правда ли?
Итак, идеальная монетка. Выигрыш равен размеру ставки. Вероятность выигрыша 0.5. Формула Келли говорит, что оптимальная ставка в этом случае равна нулю. Т.е. при бесконечно длинной игре и конечном капитале рано или поздно мы нарвемся на нежданчик.
Почему нарвемся?
Потому что среднее суммы равно сумме средних, т.е. в данном случае нулю, а дисперсия суммы равна сумме дисперсий, т.е. возрастает пропорционально количеству ставок N в серии.
Соответственно, среднеквадратическое отклонение возрастает пропорционально корню квадратному из N и рано или поздно достижение нулевой границы капитала станет почти достоверным фактом.
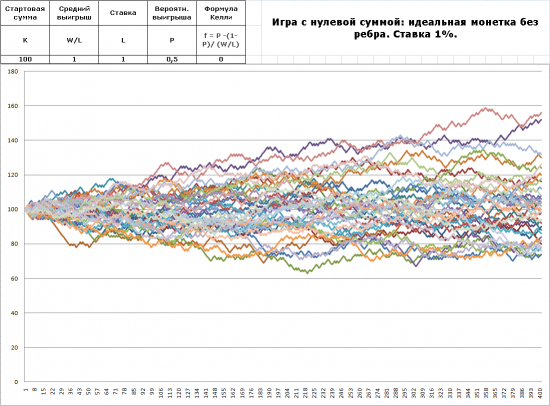
Рис.1.1. Идеальная монетка. Ставка 1% от игрового капитала.
Это иллюстрирует и результат моделирования. На рисунке 1.1 у нас приведены результаты 40 серий по 400 последовательных ставок в размере 1% от имеющегося игрового капитала.
Конечный результат складывается как повезет. Возможен как выигрыш, так и проигрыш. Исход в целом игры случаен, шансы дожить до конца серии из 400 ставок достаточно высоки.
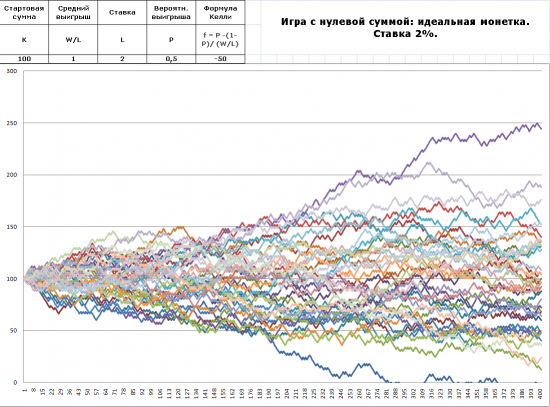
Рис.1.2. Идеальная монетка. Ставка 2% от игрового капитала.
При ставке 2% выжить в игре становится сложнее, но и выигрыш при удачном стечении обстоятельств больше.
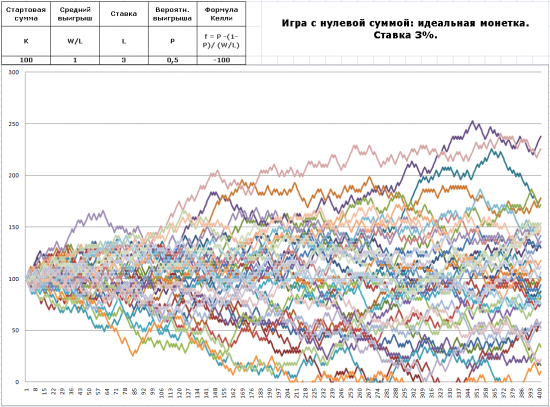
Рис.1.3. Идеальная монетка. Ставка 3% от игрового капитала.
При ставке 3% шансы на вылет еще больше возрастают, ну т. д.
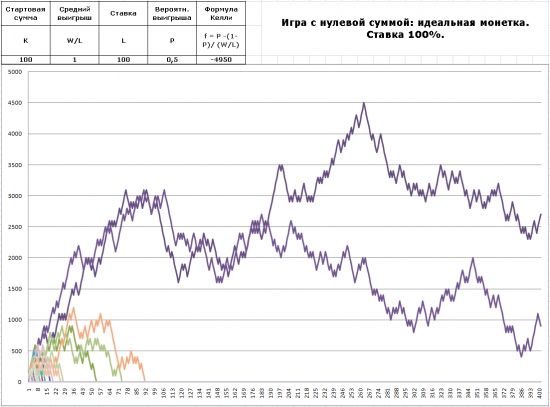
Рис.1.4. Идеальная монетка. Ставка 100% от игрового капитала. «На всю котлету».
Можно ли играть «на всю котлету» и остаться в плюсе? Можно. если повезет. В приведенном примере аж два варианта из сорока возможных дожили до финала. Но это тоже случайность. Бывало и три варианта доживали, бывало и не одного. Главное вовремя остановиться при успешной серии. А это как правило не получается.
В следующей публикации мы рассмотрим варианты игры с нулевой суммой при использовании мартингейла и антимартингейла.
=======================================================================================
Робот продолжает «пилить» золото. Закрыл с убытком продажи и снова покупает. :)
Мониторинг торгового робота.
Всем удачи!!!
SWT-метод. Теория и практика применения
Параметры волн SWT-метода

Чтобы излагаемый материал был более наглядным я сконструировал небольшой симулятор игр (на экселе), который показывает ожидаемый результат серии ставок (сделок) с заданной статистикой.
Сразу замечу, что в торговле все намного сложнее, потому что в отличие от классической игры с заранее заданным набором исходов торговая практика намного богаче.
Если в игре ставка это проигрыш и он заранее известен, а также известен выигрыш при благоприятном исходе, то в торговой практике все выглядит немного по другому.
Даже если вы заранее задали размер риска на сделку, и даже если размер риска у вас нормирован для всех сделок с любыми инструментами (это возможно и это единственно правильный подход при грамотном ММ), все равно набор исходов ставки (сделки) намного богаче:
— позиция закрыта ордером тейк-профит (этот вариант можно отнести к исходу с выигрышем в классической игре);
— позиция закрыта ордером стоп-лосс (этот вариант можно отнести к исходу с проигрышем в классической игре);
— позиция закрыта по рынку с прибылью меньшей, чем тейк-профит;
— позиция закрыта по рынку с убытком, меньшим, чем стоп-лосс.
Два последних случая портят красивую картинку, но начнем мы с классической теории игр и первой у нас будет игра с нулевой суммой — идеальная монетка без ребра, вероятность выпадения орла и решки одинакова. Выигрывает либо тот либо тот вариант. Комиссия (доля казино или иного заведения) равна нулю.
В дальнейшем у нас будет использоваться следующая система обозначений:
К — капитал, стартовая сумма игры.
L — размер ставки, потери при проигрыше.
R=W/L — отношение выигрыша к проигрышу.
P — вероятность благоприятного исхода.
f=(P(R+1)-1)/RL — формула Келли, связывающая размер оптимальной ставки с условиями игры (огромное спасибо ПBМ за указанную ошибку в формуле).
Если известно f, то
Lopt=f*K.
Знакомо, не правда ли?
Итак, идеальная монетка. Выигрыш равен размеру ставки. Вероятность выигрыша 0.5. Формула Келли говорит, что оптимальная ставка в этом случае равна нулю. Т.е. при бесконечно длинной игре и конечном капитале рано или поздно мы нарвемся на нежданчик.
Почему нарвемся?
Потому что среднее суммы равно сумме средних, т.е. в данном случае нулю, а дисперсия суммы равна сумме дисперсий, т.е. возрастает пропорционально количеству ставок N в серии.
Соответственно, среднеквадратическое отклонение возрастает пропорционально корню квадратному из N и рано или поздно достижение нулевой границы капитала станет почти достоверным фактом.

Рис.1.1. Идеальная монетка. Ставка 1% от игрового капитала.
Это иллюстрирует и результат моделирования. На рисунке 1.1 у нас приведены результаты 40 серий по 400 последовательных ставок в размере 1% от имеющегося игрового капитала.
Конечный результат складывается как повезет. Возможен как выигрыш, так и проигрыш. Исход в целом игры случаен, шансы дожить до конца серии из 400 ставок достаточно высоки.

Рис.1.2. Идеальная монетка. Ставка 2% от игрового капитала.
При ставке 2% выжить в игре становится сложнее, но и выигрыш при удачном стечении обстоятельств больше.

Рис.1.3. Идеальная монетка. Ставка 3% от игрового капитала.
При ставке 3% шансы на вылет еще больше возрастают, ну т. д.

Рис.1.4. Идеальная монетка. Ставка 100% от игрового капитала. «На всю котлету».
Можно ли играть «на всю котлету» и остаться в плюсе? Можно. если повезет. В приведенном примере аж два варианта из сорока возможных дожили до финала. Но это тоже случайность. Бывало и три варианта доживали, бывало и не одного. Главное вовремя остановиться при успешной серии. А это как правило не получается.
В следующей публикации мы рассмотрим варианты игры с нулевой суммой при использовании мартингейла и антимартингейла.
=======================================================================================
Робот продолжает «пилить» золото. Закрыл с убытком продажи и снова покупает. :)
Мониторинг торгового робота.

Всем удачи!!!
SWT-метод. Теория и практика применения
Параметры волн SWT-метода
164 |
Читайте на SMART-LAB:

Совкомфлот: танкеры сошли с якоря - текущий год будет ЛУЧШЕ предыдущего, вопрос насколько и стоит ли покупать акции?
Совкомфлот отчитался за 4-й квартал 2025 года — компания продолжает работать в 0 на операционном уровне (всему виной прощальные SDN санкции...
17:30
теги блога Николай Скриган
- AUDUSD
- bitcoin
- BRN
- DAX
- DeepSeek
- ES
- eurusd
- forex
- GBPUSD
- Gold
- MM
- nzdusd
- S&P500
- S&P500 фьючерс
- Silver
- SWT-Robot
- SWT-метод
- SWT-метод-Мастер-класс
- SWT-робот
- USDCAD
- USDJPY
- USDRUB
- usdrur
- WTI
- алгоритмическая торговля
- алготрейдинг
- Анализ трендов
- аналитика
- безбашенная торговля
- бизнес
- биржа
- биткоин
- брент
- брокеры
- вопрос
- газ
- голодание
- доллар
- доллар - рубль
- Доллар рубль
- дурные деньги
- ДЦ
- Евро
- жизнь
- жизнь как она есть
- здоровье
- ЗОЖ
- золото
- ИИ
- Индикаторы SWT
- искусственный интеллект
- Казино в мире финансов
- коронавирус
- кредитное плечо
- криптовалюта
- Криптовалюты
- механические торговые системы
- мозг
- мониторинг
- нефть
- обучение
- общество
- околорынок
- опрос
- оффтоп
- позиционная торговля
- Полигон лудомана
- политика
- прогноз
- проект на миллион
- психология
- Разное
- риск менеджмент
- Риски
- Робот
- роботы в биржевой торговле
- рубль
- рынки
- саморазвитие
- серебро
- смартлаб
- Тестируем "Грааль"
- технический анализ
- тильт
- торговая тактика
- торговые роботы
- торговые сигналы
- торговые стратегии
- торговый робот SWT
- трейдеры
- трейдинг
- ТС-100500
- убить лудоманию
- форекс
- ФРС
- фундаментальный анализ
- Фьючерсы
- экономика
- экстремальный трейдинг
- юмор





















Мы просто рассматриваем, как влияет риск на исход игры с жесткими, заранее известными правилами.
МОЙ ПЕРВЫЙ «ГРААЛЬ»
www.mql5.com/ru/articles/1413
+AG6+ЕСЛИ(СЛЧИС()<$H$4;$D$4*$F$4;-$F$4)
$H$4- вероятность
$D$4*$F$4 — W
$F$4 — L
AG6 — игог предыдущей ставки
Формула келли написана в тексте
Если хотите готовую таблицу, выложу на форуме.
traders-union.ru/forum/showthread.php?t=131988&page=13&p=2334413&viewfull=1#post2334413
Проверил ссылку, что-то некорректно работает. Файл выложен в последнем сообщении темы.
P.S. По этой ссылке можно качнуть не переходя на форум:
traders-union.ru/forum/attachment.php?attachmentid=13875&d=1445958579
есть wiki: ru.wikipedia.org/wiki/Формула_Келли
там говорится что формула Келли
f= p/B — q/A (1). если в ваших терминах, то f = P/L — (1-P)/W,
и я никак не могу понять как из этого получается f = P-(1-P)/(W/L).
хотя если вашу формулу раскрыть, будет f = P — (1-P)*L/W = L*(P/L — (1-P)/W), т.е. ваша f в L раз отличается от вики?
в случае идеальной монетки оптимальное f тоже будет равно нулю.
а вот в других случаях заметно больше.
вобщем я действительно запутался
Но сути моделирования это не меняет.
Там формула не используется.
В вики считается множитель к размеру ставки, у меня значение ставки.
По формуле в вики получаем f, который нужно умножить на L.
По ранее приведенной у меня формуле не зависит: f=P-(1-P)/R сразу необходимое значение.
В этом легко убедиться поиграв с размером ставки, от которой ничего не должно в принципе зависеть. Все определяется статистикой и отношением W/L.
Если значение формулы в вики умножить на L то все будет ОК.
Текст уже редактировать не могу, время истекло.
при продолжительной игре 50/50 нарвешься на серию (серии) убытков вероятность которых низка но все же возможна, поэтому формула и рекомендует ноль
может быть ткнете носом в раздел теории непонятен переход:
Почему нарвемся?
Потому что среднее суммы равно сумме средних, т.е. в данном случае нулю, а дисперсия суммы равна сумме дисперсий, т.е. возрастает пропорционально количеству ставок N в серии.
Соответственно, среднеквадратическое отклонение возрастает пропорционально корню квадратному из N и рано или поздно достижение нулевой границы капитала станет почти достоверным фактом.
если случайная переменная стационарная (дисперсия постоянная) то не должно быть никаких увеличений СКО
ММ — это вообще отдельная категория, никаким образом к рынку не относящаяся. Абсолютно без разницы, каким образом формируются выигрыши и проигрыши. Есть игра и ее характеристики.
Если предположить, что исход сделки трейдера описывается бросанием монетки, то тут никакие ухищрения не помогут: вероятность заработать/потерять деньги останется постоянной 50/50. ММ поможет только увеличить время в течении, которого трейдер заработает или сольёт депозит.
Кто сказал, что у каждого трейдера вероятность прибыльно и убыточной сделок одинакова? Это только первый вопрос.
Кто сказал, что размер выигрыша и проигрыша одинаков? Это второй вопрос.
Кто сказал, что размер выигрыша постоянен? Это третий вопрос...
Продолжать лень.
Я же говорю, я разговариваю сейчас о монетке. А вы о чем-то другом.
К чему написал?
В основном для себя, наверное. Я сейчас изучаю нюансы методов управления капиталом, а лучший способ что-то понять, это сформулировать на бумаге. Вот и формулирую, начиная с простейших задач, чтобы начать издалека, с тех пор «когда земля еще была тепленькая» и рассмотреть, как влияют на исход финансовых игр различные условия по ММ.
Насколько это будет применимо к торговле решать не мне. Испытания Бернулли с дуальным фиксированным результатом и торговля плохо сочетаются. Но какие-то общие закономерности будут проявляться и в торговле, хоть и со своими нюансами.
(Если помните, то это Hunter01 из Вашей прошлой форумной жизни).
Мой блог (не смартлабовский) никуда не делся. 6 лет на одном и том же месте.
Плюсану вам в профиль, чтобы поднять рейтинг с нуля :)
Келли говорит: «ставить в каждой сделке 1% от текущего капитала». При таком подходе эквити может стремиться к 0, но никогда его не достигнет.
Соответственно, в примере «на всю котлету» у Вас все эквити должны обрываться в 0. Потому что невозможно выиграть в монетку 400 раз подряд.