Блог им. IgorK_23a
Начинающий алготрейдер -- чем чаще сделки, тем хуже?..
- 29 июля 2025, 12:46
- |
С утра пораньше возникла мысль насчет сравнения стратегий с частыми и редкими сделками на чувствительность к издержкам.
Поставлю задачу так: если нужно добиться нетто (то есть с учетом издержек) доходности в R_net, какая должна быть брутто доходность R_gross?
Формулы для случая рекапитализации:


r — доходность одной сделки, s — издержки с одной сделки.
Из второй формулы выражаем r и подставляем в первую, получаем:

Чтобы исследовать эту зависимость, зафиксируем R_net = 50% (хочу 50% в год чистыми), s=0.2% (издержки с одной сделки), построим график от n:

Например:
При числе сделок 100 в год, нужен брутто в 100%
При числе сделок 300 в год, нужен брутто в 200%
При числе сделок 500 в год, нужен брутто в 350%
— чтобы достичь нетто в 50%.
Асимптотически при n->inf имеем:
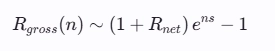
Гросс зависит экспоненциально от количества сделок!
Имеем два «парадоксальных» вывода:
— Частые стратегии менее выгодны, чем редкие
— В частых стратегиях лучше использовать фиксированную позицию, а не рекапитализацию.
Без рекапитализации формула выглядит так:

Конечно, это идеализированная модель: согласно ей, выгоднее всего сделать ровно одну сделку с заданной прибылью, тогда издержка будет минимальна; но заставляет задуматься, что, скорее всего, в каждой стратегии есть какой-то оптимум на количество сделок:
— При слишком маленьких n не отслеживается рыночная динамика
— При слишком больших n издержки съедают доходность.
И у меня есть ощущение, что для «классических» (не HFT) стратегий оптимум лежит скорее в часовых/дневных интервалах, а не в минутных.
Критикуйте!


теги блога IgorK
- bitcoin
- carry trade
- copilot
- LEI
- macd
- MOEX
- SP
- usdtry
- акции
- алготрейдинг
- арбитраж парный трейдинг
- биткоин
- волатильность
- золото
- издержки
- ИИ
- инвестирование
- инвестиции
- искусственный интеллект
- криптовалюта
- макро показатели
- макроэкономика
- марковиц
- машинное обучение
- Модели рынка
- моделирование
- монте-карло
- обзор книг
- облигации
- облигациии
- Оптимизация портфеля
- опцион
- опционы
- Парный трейдинг
- парный трейдинг
- пифы
- портфель инвестора
- портфель марковиц
- технический анализ
- торговые роботы
- трейдинг
- Турция
- турция рынок
- форекс
- фьючерс
- цикличность рынка
- экономика Турции




















чтоб гарантировать исполнение сделки в тестировщике надо выствить параметр сделка при пересечении цены а не просто при касании цены...
но опять же есть америка и тот же букинг 5000баксов за акцию при комиссе 0.35 цента
Я сделал (не всегда верное) предположение, что количество сделок обратно пропорционально величине дискретизации — но только в последнем предложении, все остальные рассуждения использовали только величину «количество сделок».
привязываться к таймфрейму вместо величины тейкпрофита.
Может не в курсе, просто поверьте -
на м1 профит может быть больше, чем на н1 и тогда издержки пох.
Знаю что говорю, т.к. уже несколько лет торгую в основном м1.
Еще один вариант, когда издержки пох — когда сделок м1 много и они с явным перевесом выигрышных.
Издержек математически «катастрофически» много,
но профита больше и на старших ТФ столько не заработать!
Жалею, что я не математик,
но иногда это помогает приходить к таким вот выводам.
А вообще у вас голая теоретизьма.
Так НЕЛЬЗЯ сравнивать, сравнивать надо ТС, а не коней в вакууме.
Тогда параметры ТС сами приведут вас к тому, что я написал.
Ваши нетто-брутто о том же, но приводят к неверным выводам.
Если стратегия частотная (300 сделок в год и больше), то тестировщик стратегий (который не учитывает издержки) должен показать выдающиеся результаты — 150% годовых и больше, чтобы такую стратегию можно было рассматривать как перспективную, а не выкидывать сразу.
Это реально очень большой процент, он разошелся с моими интуитивными ожиданиями.
Что-то с вами не так… Прям горе от ума…
VladMih, вы, наверное, не поняли моего утверждения. Я не указывал дискретность интервала. Смотрите, что я утверждаю.
В предположении, что:
1) Стратегия делает 300 сделок в год (неважно, на m1, h1 или d1)
2) Издержки с одной сделки — 0.2%
3) Прибыль реинвестируется
— то для чистой годовой прибыли в 50% на тестировщике должно показывать 150% (без симуляции издержек, спреда и проскальзывания). Если меньше, то эту стратегию нельзя использовать в реале.
Вы с чем-то здесь несогласны? Возможно, предпосылки вам кажутся нереальными? Либо полученные цифры расходятся с вашим практическим опытом? Пожалуйста, конструктивно.
Вам бы поторговать активно хотя бы годик другой,
без этого вам что-то объяснять нереально.
Попробую зайти с другой стороны (последняя попытка).
Вникните в простейший факт: ПОДАВЛЯЮЩЕЕ большинство ПРОП-трейдеров торгуют внутри дня и большинство на минутках. Делают большие обороты и профиты без нарушения ММ(!) (иначе с ними быстро попрощаются).
Не буду обсуждать с вами о каких процентах идет речь
и тем более не буду доказывать, что возможно и больше указанной вами цифири. Главное, что пытаюсь донести — огромное количество так работают, зарабатывают большие деньги и им глубоко насмного на ваши выкладки как правильно работать с каким-то убогим тестером.
Что у вас там за убожество, которое издержки не учитывает?
Я таких даже не видел! — Выкиньте его, не позорьтесь!
Упрощу до максимума: если издержка с одной сделки 0.2%, а сделок было 300, то убытки с издержек будут 300 * 0.2 = 60%.
Чтобы чистая прибыль была 50%, грязными должно быть 50+60=110%.
Всё. Не понимаю, с чем вы спорите, с базовой арифметикой?
Я же совершенно не оспариваю тот факт, что на таких стратегиях можно заработать. Наверняка можно, и не только 110%, а и гораздо больше. Но конкретно мои стратегии такого результата не показывают, поэтому я вижу смысл для себя уходить в стратегии с меньшим числом сделок в год (70-80 сделок показало на моей стратегии оптимальный результат); а этот подсчет использую просто как фильтр.
Калькулятор из вас выйдет отменный!
Но меня вы не услышите. О причинах я писал выше.
Без теории практикам (мне) трудно,
а теоретикам без практики невозможно.
Вы начнете на всё смотреть другими глазами, когда поторгуете.
Желательно СИСТЕМНО.
Надеюсь, вам понятно, что я не просто так назвал вас новичком?
Просто это… очевидно. Даже не представляете до какой степени!
Зависимость от R_net обратная. Вот график при фиксированном gross=100%.
И ваше Rnet станет отрицательным. Соответственно, Rgross по экспоненте повалится к минус 1.
Недостаточно считать только по средним, нужно выбросы как-то учитывать и ограничивать.
Второй пост говорит о том, что при росте n неизбежно станет r<s для той же ТС.
svgr, ваше замечание очень просто обойти. Просто предположим, что r — это среднее геометрическое (а не арифметическое) за все сделки, тогда все формулы остаются точными.
Среднее геометрическое приближается к среднеарифметическому при уменьшении волатильности r.
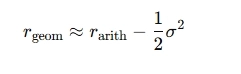
Второе замечание про рост n: оно говорит о том, что частотные стратегии еще хуже, чем эта идеальная модель, то есть основной вывод, что менее частотные стратегии лучше, сохраняется.
но у автора в выводах совсем про другое: