Для большинства трейдеров свечные графики различного таймфрейма это и есть рынок, там скрывается все — и тренд и боковик и хитрый маркет мэйкер с глобальным кукловодом. Начнем с простых фактов, за одну сессию 2012.11.07 на фьючерсе Ri ядро биржи обработало 10 449 043 транзакций или примерно 12 000 транзакций в минуту, одна свечка самого «высоко частотного» минутного таймфрема скрывает за собой огромное количество более элементарных действий. Поэтому мы спустимся на самый низкий уровень того, что происходит на бирже и начнем оттуда.

    Можно долго рассказывать про то как устроена биржа, про промежуточные сервера и другие части «транспортной» инфракстуры, какие задержки они вносят при путешествии заявки, но в конце пути любая заявка попадает в ядро биржие, где непосредственно происходит то ради чего все собственно и затевалось — сведение(matching). И на этом уровне, в смысле формата данных и производимых элементарных действий, FORTS мало чем отличается от той же CME или любой другой современной биржи. Входной поток состоит из заявко двух типов, на вставку(insert) и отмену(cancel). Бьете вы по рынку или выставляете заявку в глубь стакана — для ядра нет разницы, все это в конечном итоге преобразуется в заявку на вставку, которой присваивается свой уникальный идентификатор. Другой тип заявок — на отмену, позволяет убрать часть(или всю) предшествующей заявки на вставку. Ядро принимая на входе поток состоящий из заявок на вставку и отмену, создает поток сведенных сделок, каждая сведенная сделка связана с двумя заявками участвующих в сделке. Исходя из полученного потока, затем строятся стаканы, и тиковые данные(сведенные сделки), которые рассылаются пользователям(к примеру на RTS срезы стаканов строятся с периодичностью 30 миллисекунд), и лишь затем тики преобразуются в красивые свечки, отображаемые на экране. Поток данных содержащий заявки на вставку, отмену и сведенные сделки, на FORTS называется Full Order Log.

( Читать дальше )

Попробуем сделать простейшую стратегию для долгосрочного инвестирования. В качестве рабочего будем использовать дневной таймфрейм. Вся суть стратегии будет заключаться в простейшей идеи, что падение рынка обычно связанно с более высокой волатильностью, чем в среднем. Соответсвенно, мы будем покупать, когда волатильность ниже среднего, и выходить из лонга когда она повышается. В качестве меры волатильности будем использовать размах бара High — Low. Остается вопрос лишь в том как измерить долгосрочное среднее волатильности. Можно использовать — среднее, то есть скользящую среднюю взятую за определенный период. Но так как мы имеем дело с распределением с тяжелыми хвостами, среднее будет плохой оценкой центра распределения. Поэтому будем использовать робастную оценку центра распределения — в нашем случаи это будет медиана, или более точно, скользящая медиана взятая с большим окном. Наши рассуждения достаточно напрямую транслируются в код на WealthLab:
 

using System.Collections.Generic;
using System.Text;
using System.Drawing;
using WealthLab;
using WealthLab.Indicators;

namespace WealthLab.Strategies
{
	public class MyStrategy : WealthScript
	{
		private StrategyParameter smaPeriod;
		public MyStrategy()
		{
			smaPeriod = CreateParameter("Range Sma Period", 1, 1, 50, 1);      
			
		}
		
		protected override void Execute()
		{
			DataSeries range = High - Low;
			DataSeries rangeSma = new WealthLab.Indicators.SMA(range, smaPeriod.ValueInt, "sma");
			DataSeries signal = rangeSma -  new WealthLab.Indicators.Median(range, 200, "median");
			
			for(int bar = 0; bar < Bars.Count; bar++)
			{				
				if (IsLastPositionActive)
				{
					//code your exit rules here
					if (signal[bar] > 0)
						SellAtMarket(bar + 1, LastPosition, "sell");
				}
				else
				{
					//code your entry rules here
					if (signal[bar] < 0)
						BuyAtMarket(bar + 1, "buy");
				}
			}
		}
	}
}

( Читать дальше )

Обещал выложить книжки по математике, начиная от азов, теорвера, и заканчивая моделями числовых рядов и машинным обучением.
Структура примерно такая:
1. basic  - матан, линейная алгебра, если прогуляли/никогда не знали/ничего не помните
2. probability — базовая теория вероятности/статистика
3. time_series — стандартные(в основном стационарные) статистические модели числовых рядов
4. advanced — про продвинутые модели и машинное обучение
bonus. cointegration/r/bayes — про коинтеграцию, R (пакет для стат. расчетов), и Байесовскую статистику

Ссылка на книги  

Собственно, понятие коинтеграции и лежало, в основе статистического арбитража, который только начал появлятся в конце 80-х и позволил первопроходцам из JP Morgan, нарубить не мало денег, пока…, но об этом в конце статьи. Поэтому в этот раз мы поговорим, про коинтеграцию, что это такое, зачем и почему. Но начнем из далека и рассмотрим такие статистически понятия как порядок интеграции процесса, и фиктивной (spurios) регрессии, которые и лежат в основе. 

Рассмотрим для начала простейший процесс, гауссовский шум:


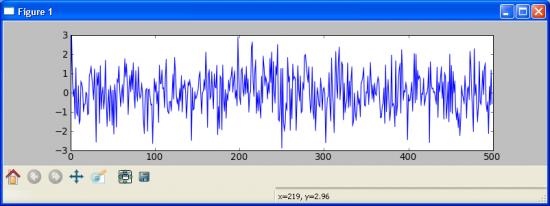
 Теперь построим его кумулятивную сумму, то есть возьмем значения и последовательно их сложим, таким образом получим что Y_i = sum k = 0..i X_k, где X_k — это исходный гаусовский шум, Y_i — результирующий процесс. То есть в данном случаи взяли шум и его проинтегрировали, таким образом получив случайное блуждание. Так же мы можем повторить данный процесс еще раз, но на этот раз взяв в качестве исходных значений, полученное нами на предыдущем шаги случайное блуждание. Таким образом получим (сверху — интеграл шума, случайное блуждание, снизу — повторная сумма но на этот раз взятая по случайному блужданию):

( Читать дальше )

Четыре годные книжки по этой тематике.
http://narod.ru/disk/44732842001.342fa2327b2ad1d65e7e1143b7a54769/prob%20theory.zip.html
 
 

Обещанное продолжение. Предыдущий пост из серии: http://smart-lab.ru/blog/43277.php 

В чем собственно смысл понятия авторегрессивности/автокорреляции/персистентности. Расмотрим простейший процесс в котором последующие приращения зависят от предыдущего. Обозначим приращение в момент времени t — X_t, в момент времени t + 1 — X_t+1. Соответственно мы хотим, чтобы приращение в момент времени t+1, каким то образом зависело от предыдущего t. Если выразить такую зависимость качественно, то у нас есть два варианта.

1) первый вариант, мы предполагаем что положительное приращение X_t должно увеличивать вероятность положительного приращения в следующий момент времени X_t+1, аналогично для  отрицательного. Проще говоря Х_t и X_t+1 положительно скоррелированны. Такая модель является «трендовой, персистентной», то есть покупая/продавая то что растет/падает мы смещаем вероятность выигрыша в свою сторону.

2)  второй вариант, мы предполагаем что положительные приращения X_t должны увеличивать вероятность отрицательных в момент времени X_t+1, а отрицательные приращения — положительных. То есть X_t и X_t+1 отрицательно скоррелированны. Такая моделья является «контр трендовой, анти-персистентной», то есть продавая то что выросло и покупаю то что упало, мы получаем статистическое преимущество. 

( Читать дальше )

Оригинал статьи:  http://www.frbsf.org/publications/economics/letter/2011/el2011-26.html

Перевод на слоне:
http://slon.ru/economics/eho_voyny_nakonec_dokatilos_do_birzhi-651960.xhtml


В чем суть, два товарища из Сан Франциского ФЕДа: Zheng Liu is a research advisor in the Economic Research Department of the Federal Reserve Bank of San Francisco, и Mark M. Spiegel is a vice president in the Economic Research Department of the Federal Reserve Bank of San Francisco, решили провести исследование на тему, как влияет отношение стареющего населения на P/E. Конкретно в качестве коэффициента старения они взяли логарифм отношения группы 40–49 лет к 60–69 далее M/O. 

( Читать дальше )

Попросили объяснить что такое персистентность без специальных терминов и как она связана с трендовостью рынка. Совсем, без терминов вряд ли получится, но если их минимизировать, достаточно понятия — плотности вероятности. 

Что такое плотность вероятности? Это функция интеграл интервала которой, дает нам вероятность попадания в этот интервал. Или в простейшем случаи, если мы рассматриваем ее эмпирическую оценку в виде гистограммы распределения это будет просто частота попадания в набор фиксированных интервалов. 
Для примера рассмотрим гистограмму нормального распределения.

 

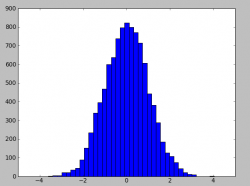
Собственно что мы видим — разбиение на набор фиксированных интервалов, затем подсчет попадания каждого значения в тот или иной интервал, который дает частоту. Если мы хотим посчитать частоту попадания в бОльший интервал например от 0 до 2, то нам необходимо сложить(проинтегрировать) частоту попадания во все маленькие интервалы внутри этого отрезка [0, 2]. Таким образом плотность вероятности дает возможность, зная интервал, получить вероятность попадания в него. Или если рассматривать на более «интуитивном» уровне — показывает какие значения выпадают более часто, а какие менее. В приведенном примере, наиболее часто выпадают значения вокруг нуля распределения и затем оно постепенно спадает. 

( Читать дальше )

Если немного «перепеть» классика, то тренд характеризуется, тем что каждый лоу выше/ниже предыдущего при аптренде/доунтренде. Попытаемся проверить насколько эти представления актуальны. Для этого возьмем дневки Ри, за 2010-2011 год и посчитаем разницу между лоу текущего дня и предыдущего, то есть LowDelta = Low[Day] — Low[Day — 1]. Нас будет интересовать насколько значения этого ряда, автоскоррелированы, то есть при аптренде если верить теории Доу, положительные значения LowDelta должны следовать за положительными, а отрицательные за отрицательными. Соответственно получим числовой ряд этих LowDelta выглядящий следующим образом:


На первый взгляд — просто шум, но мы немного углубимся в его анализ. ) Нас будет интересовать насколько значения этого ряда, автоскоррелированы, то есть при аптренде если верить теории Доу, положительные значения LowDelta должны следовать за положительными, а отрицательные за отрицательными. Чтобы как-то выразить эти соотношения математически, введем второй фактор — значение LowDelta, за предыдущий день обозначим его LagLowDelta = Lag(LowDelta, 1) = Low[Day — 1] — Low[Day — 2]. Теперь нарисуем, пары значений (LowDelta по X, LagLowDelta по Y):

( Читать дальше )