SMART-LAB
Новый дизайн
Мы делаем деньги на бирже
Блог им. tomtomtom
Такого на лчи еще небыло
- 30 ноября 2022, 13:05
- |
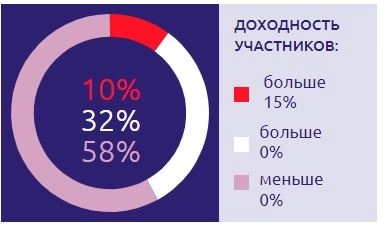
В каких учебниках это видано чтобы зарабатывающих и сливающих было 50/50? Думаю после февраля народ стал меньше рисковать.

531
Читайте на SMART-LAB:

Как заработать на росте цен на удобрения
Дарья Фёдорова Конфликт на Ближнем Востоке и перекрытие Ормузского пролива вызвали ралли не только цен на нефть и газ, но также алюминий и...
18:38
Курс доллара на Forex впервые за два месяца превысил 80 рублей
Доллар в паре с рублем на международном валютном рынке достиг психологически значимой отметки 80 впервые за два месяца, однако примерно через...
15:01
теги блога tomas_kub ✔️
- 2 НДФЛ
- CNY
- CNYRUB
- CRM
- FORTS
- qscalp
- quik
- Ri
- S&P500
- Si
- sim4
- usd
- акции
- банки
- бкс
- брокеры
- валюта
- валюты
- возврат налога
- девальвация рубля
- доллар
- доллар рубль
- евро
- евродоллар
- золото
- инвестиции
- итоги года
- Итоги месяца
- Итоги недели
- квалифицированный инвестор
- ключевая ставка ЦБ РФ
- лчи
- лчи 2021
- ЛЧИ 2022
- лчи 2023
- мир
- мирные переговоры
- налоги
- налогообложение на рынке ценных бумаг
- натуральный газ
- нефть
- нефть Brent
- НКЦ
- обвал
- онлайн торговля на FORTS
- опрос
- опцион
- опцион Si
- опционы
- оффтоп
- Портфель инвестора
- прямой эфир
- реальная торговля
- рецензия на книгу
- робот для Quik
- РТС
- рубль
- рубль доллар Si
- Рубль Евро
- рубль юань
- си
- сигнал шорт
- Срочный рынок
- срочный рынок FORTS
- стоп лосс
- торговля
- торговля на бирже
- торговля на рынке
- торговля онлайн
- торговля фьючерсами
- торговые роботы
- торговые сигналы
- торговый софт
- трейдинг
- Украина
- форекс
- фьючер доллар-рубль
- фьючерс РТС
- ЦБ РФ
- юань





















Смоделируйте на монетке и все увидите. Скажем, 1000 участников, по тысяче на рыло, ставка рубль. Посмотрите сколько останется в живых через год интенсивной торговли…
Рассмотрим простейший случай, 1024, человека, у каждого по одной монетке. Каждый находит себе пару и делают противоположные ставки. Уже осталось 512 чел.
Если поставить весь выигрыш, то пойдет по нисходящей 256, 128, 64,....2, 1. Все деньги у одного за 10 ставок.
Если у них больше денег и ставка не на все, то это замедлит процесс, но не изменит результат.
Ну кто же играет «пан или пропал»? Возьмем проще: два игрока со 100 руб. начинают играть в «орлянку» со ставкой по рублю. Играют 1000 бросаний. Так вот, вероятность того, что один из них проиграет больше 50% капитала (второй, соответственно, выиграет), 1.4*10-3. А то, что один из них «сольется в нуль» 1.8*10-10 Для 1000 руб. и 10000 бросаний все еще лучше: первая вероятность меньше 10-21, вторая меньше 10-86 .
Ну а вероятность получить прибыль 1/2.
Если возьмем 1000 игроков с 1000 руб., каждый из которых делает по 10000 бросаний, при каждом бросании случайно выбирая контрагента, то для любого одного отдельно взятого игрока вероятности будут те же, что и выше.
Через некоторое время в существенном выигрыше оставались ~20%. Остальные, либо проигрывали, либо выигрыш был несущественным.
Игры с выбыванием участников, это несколько другие игры.
При случае, когда время будет, повторю с графиками развития событий.