SMART-LAB
Новый дизайн
Мы делаем деньги на бирже
Блог им. Kot_Begemot
Создаём рынок волатильности по теории оптимальной улыбки (Market Making Volatility by STO)
- 02 октября 2019, 12:39
- |
Сегодня мы будем выступать в качестве поставщика бесконечной ликвидности по опционам. То есть мы будем безотказно играть в игру с нулевой суммой так, чтобы, как минимум, не проиграть, а это возможно только в том случае, если мы будем продавать и покупать волатильность по цене, соответствующей седловой точке в игре покупателя и продавца, то есть по цене GTO (game theory optimal). Иными словами, мы будем заниматься непосредственно pricing'ом опционов, назначая цены put'ам и call'ам, таким образом, чтобы ни одна стратегия и ни один набор случайных, стохастических стратегий не мог получить положительное преимущество при игре с нами.
Чтобы назначать цену волатильности, для начала, не плохо было бы принять какую-либо модель волатильности. Например, это может быть модель случайного процесса, подчинённого логистическому распределению:
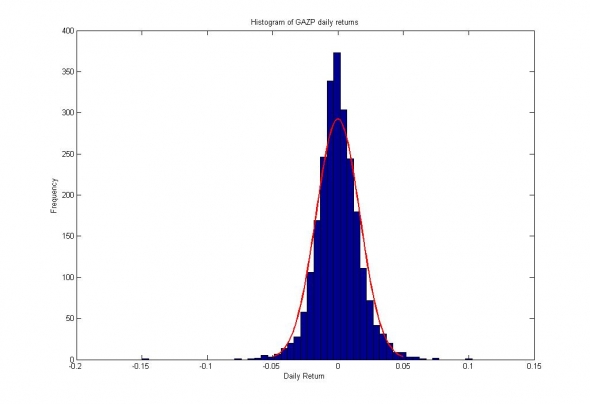
Рис.1. Распределение логарифмических приращений цен акций ПАО Газпром и их аппроксимация логистическим распределением.
или распределению Лапласа:
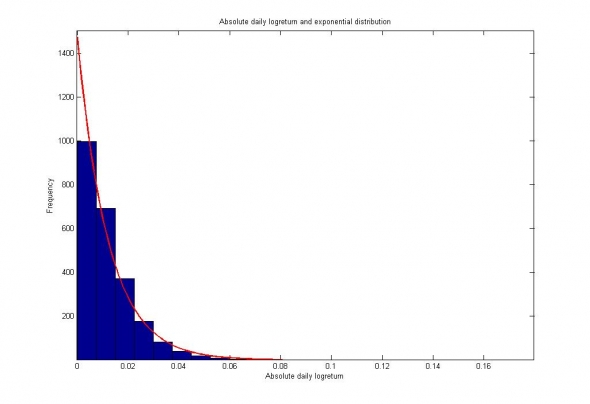
Рис. 2. Распределение абсолютных значений логарифмических приращений цен акций ПАО Газпром и их апроксимация экспоненциальным распределением.
Поскольку нам ближе безарбитражные процессы с неравномерным распределением средней мощности (волатильности) во времени (см. «Кому улыбается волатильность»), мы остановимся на втором варианте.
Экспоненциальное распределение это распределение одного параметра — m=sigma - который нам нужно оценить во времени, то есть, принимая во внимание эффект кластеризации волатильности, нам нужно оценить не только форму локального распределения приращений, но и его ширину. Иными словами, помимо самой функции распределения приращений, обладающей некоторой волатильностью (шириной), мы будем ещё учитывать и изменчивость этой волатильности во времени, то есть, непосредственно, волатильность волатильности.
Для этого мы будем пользоваться автоматически настраиваемой EWMA — 40 ( относится к классу ARCH — 40) моделью.
Исходный алгоритм принимает на вход временной ряд из последних 40 логарифмических приращений и последовательно производит действия:
- Оценивает параметры EWMA модели
- Строит саму модель и оценивает её ошибку
- Исходя из полученной модели волатильности и ошибки этой модели на IS выборке оценивает будущую волатильность и распределение ошибок будущей волатильности.
Принципиально, данная автонастраиваемая модель практически не зависит от выбора окна, но, тем не менее, даёт наилучшие результаты на окне равным двум последним месяцам (40).
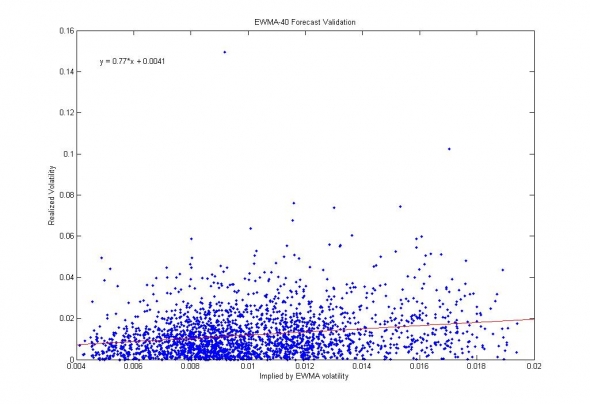
Рис. 3. Результаты прогнозирования волатильности автонастраиваемой EWMA-40 моделью. Корреляция прогноза и реализации — 77%.
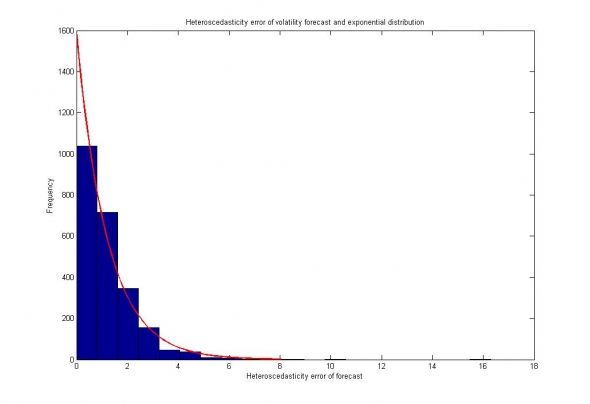
Рис. 4. Гетероскедастичная ошибка прогноза волатильности и его апроксимация распределением Лапласа (экспоненциальным).
Как видно, гетероскедастичная ошибка данной модели повторяет исходное распределение ряда, что говорит о том, что мы определили волатильность правильно, то есть, спрогнозировали непосредственно саму волатильность (ширину распределения), а не что-либо другое.
Теперь, из прогноза волатильности и его гетероскедастичной ошибки, нам осталось только получить распределение логарифмических приращений цен базового актива на ближайшее будущее и можно приступить к расчету цен опционов. Но, такой подход был бы слишком… непрофессионален, поэтому мы зашифруем простые и понятные результаты численного интегрирования экспоненциального распределения в сложную форму улыбки предполагаемой волатильности Блэка-Шоулза, павно перетекающей в дельта-хедж по Корнеру-Фишеру, а чтобы было ещё надёжней — построим не просто улыбку, а рельефную поверхность этой улыбки, протекающей в пространственно-временном континууме, свёрнутом в бублик суперструны.
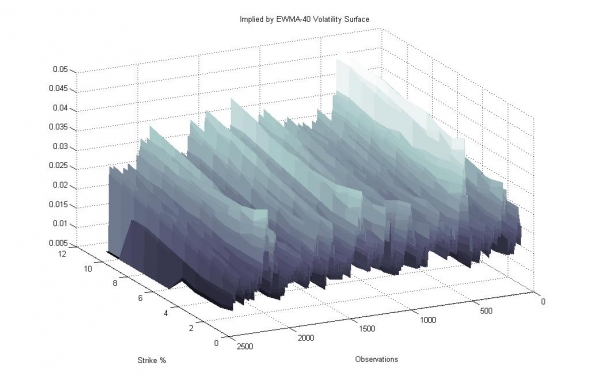
Рис. 5. Полученная поверхность IV auto-EWMA-40 моделью по Smile Theory Optimal.
Для того, чтобы убедиться в отсутствии misspricing, то есть соответствии STO цен GTO-оптимальным, безорбитражным ценам, проведём симуляцию продажи опционов квалифицированным инвесторам и рассмотрим их результирующую прибыль:
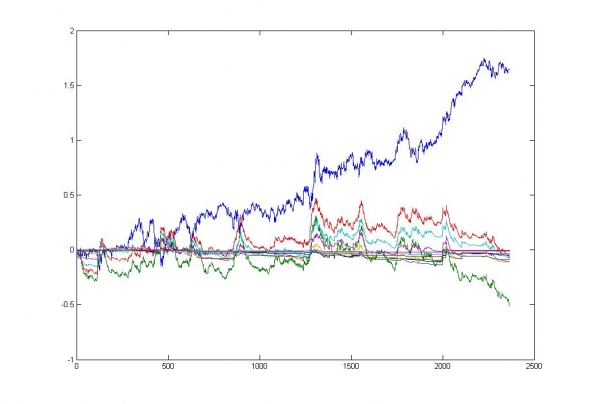
Рис. 6. Симуляция продажи стрэддлов по различным страйкам на БА — TATN. Нормированное уклонение финансового результата от нуля лежит в интервале от -0.8 до -0.16 сигма.
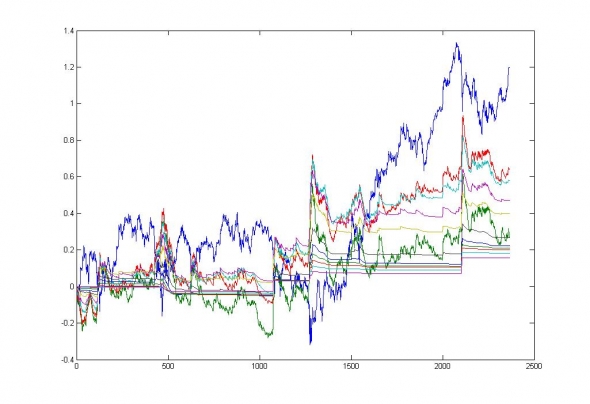
Рис. 7. Симуляция продажи стрэддлов по различным страйкам на БА — SBER. Нормированное уклонение финансового результата от нуля лежит в интервале от 0.4 до 1.4 сигма.
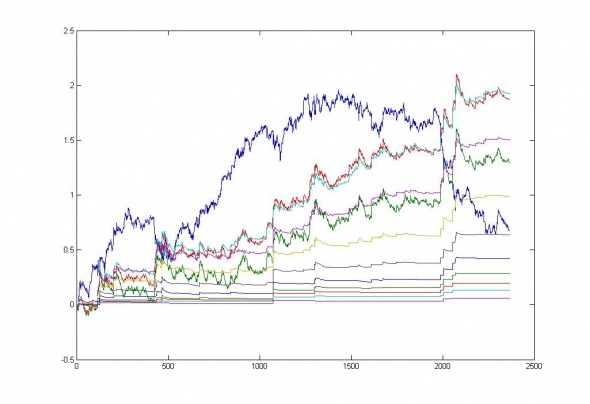
Рис. 8. Симуляция продажи стрэддлов по различным страйкам на БА — MGNT. Нормированное уклонение финансового результата от нуля лежит в интервале от 1.9 до 4.24 сигма. Что, для распределений с «тяжелыми хвостами», соответствующих стратегиям покупки стэдллов — более чем нормально.
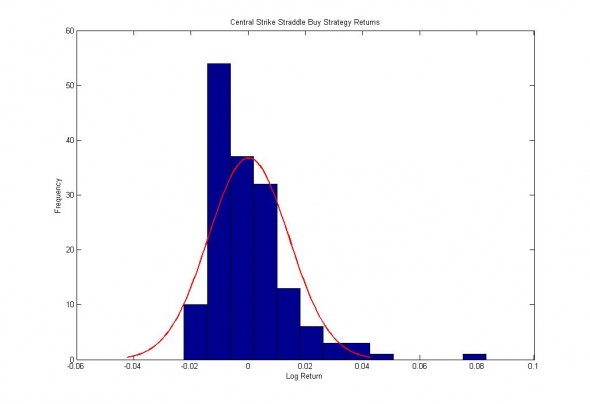
Рис. 9. Распределение прибылей и убытков от покупки стрэддла центрального страйка.
Для всех активов наблюдается схожий финансовый результат, сильно коррелированный по всем страйкам, то есть исключающий возможности misspricing'a по кривизне улыбки и соответствующий только смещённости выборки в пользу роста или падения волатильности.
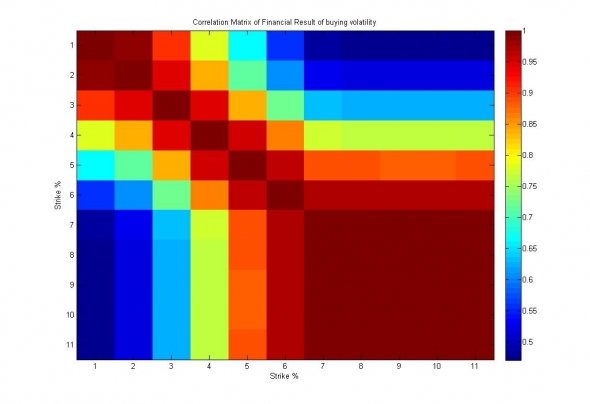
Рис. 10. Изображение корреляционной матрицы финансовых результатов покупки волатильности по разным страйкам.
Прим :
Неискушенному читателю может показаться, что вот оно — ГТО! Но это далеко не так. ГТО ГТу — рознь, если дело касается эффективности статистических оценок. Подобрать ГТО «в среднем» — легко, достаточно лишь, чтобы оно совершало локальные взаимозануляющие ошибки. Но такое, «среднее» ГТО, не смотря на свою состоятельность, будет проигрывать любому более эффективному ГТу.
3.4К |
Читайте на SMART-LAB:

МГКЛ на Smart-Lab & Cbonds PRO облигации 2.0 📍
Мы уже работаем на площадке и ждём вас на стенде МГКЛ — будем рады встрече и вопросам. 🕑 В 14:30 генеральный директор ПАО «МГКЛ» Алексей...
11:30
теги блога Kot_Begemot
- API
- cpp
- FORTS
- LUA
- Matlab
- NASDAQ
- open source
- Quik Lua
- S&P
- S&P500
- S&P500 фьючерс
- Vanguard Group
- VIX
- акции
- акции США
- алгоритмы
- алготрейдинг
- анализ временных рядов
- баффет
- волатильность
- Гордон
- доверительное управление
- долги
- игры
- инвестиции
- индекc
- интеграция
- искусственный интеллект
- Келли
- Книги
- книги о трейдинге
- корреляция
- кризис
- криптовалюта
- лудомания
- Марковиц
- матлаб
- машинное обучение
- ММВБ Акции
- наука
- нейронные сети
- облигации
- одураченные случайностью
- оптимизация
- оптимизация торговых систем
- опционы
- оффтоп
- оционы
- памм счета инвестиции
- паника
- пирамида
- ПИФы
- портфели
- Портфель
- портфельное инвестирование
- пузыри
- раздача
- рецензия
- Риски
- рэнкинг мосбиржи
- Сбербанк
- спекуляции
- статистика
- стоимостное инвестирование
- талеб
- теги не нужны
- теория игр
- торговая система
- торговые роботы
- трейдинг
- улыбка волатильности
- управляющая компания
- финанализ
- фундаментальный анализ
- фьючерс ртс
- Шарп
- шутка
- Экономика




















Смысл расчёта GTO в том, чтобы получить нулевую стратегию. А потом, как Маркет Мейкер, при желании вы можете добавить премию или комиссию.
Пока что вырабатывается методология решения проблемы поиска «нулевой» стратегии.
однако
ps. Прошу прощение, я тикеры не прочитал
И почему-то диапазон до 2 соток, для стоковых тикеров представляется как-то немного — т/фрейм точно мес. или день?
Не совсем. В заблуждение вводит непривычный масштаб графика вследствие «тяжелых хвостов» ошибок.
«betta» будет сильно отличаться от корреляции только в том случае, если диапазон (range) зависимой переменной (RV) будет сильно выше диапазона независимой переменной (ewma_IV), но так как модель авторегрессионная, то диапазон её оценки соответствует диапазону наблюдений.
Так, если убрать на графике только 2 точки — «выброса» (от тяжелых хвостов), то 77% корреляции станут намного более заметными.
Да, ТФ — 1 день. С учётом примерно линейного отображения лог.масштаба вблизи нуля в нормальный масштаб с k=1, средняя волатильность акции 1.2% в день это нормально. 10-15% — и даже 60% возникает только в случае реализации края тяжелых хвостов.
STDDEV зависимой != STDDEV зависимой.
но тогда я сразу хочу уточнить: я исходил из того, что ewma_IV (сразу отделяем от привычного IV) это текущая оценка RV, полученная классической EWMой (факт автонастраиваемости тут опустим), и ни разу не implied?
Это совсем уж точно)
Совсем ничего непонятно. Сразу видно, что разговор идёт про опционы)
Моя оценка RV это как раз Implied, потому что это не только измерение текущей волатильности, но и прогноз будущей. Ранее я сравнивал различные модели, в том числе SSA (SVD) и пришёл к выводу, что наилучшим прогнозом обладает ARCH модель:
ЕWMA здесь отвечает только за то, что коэффициенты альфа представляют из себя экспоненциальное взвешивание наблюдений во времени:
К IV Black 'n Sсholes ожидаемая волатильность никакого отношения не имеет, так как не предполагает нормального распределения логарифмических приращений и не производит, таким образом, улыбку ошибочных представлений.
То есть, если говорить о классике, то ни EWMA, ни IV к ней не имеют никакого отношения.
Работаю только в Матлаб.
В R не работаю, в Python не работаю.
это точно д.б. кот шредингера