Блог им. Kurbakovsky
О вычислении дельты опциона
- 09 марта 2019, 23:24
- |
О вычислении дельты опциона
Дискуссии о правильных и неправильных методах вычисления дельты опциона. Дошел до темы «Липкая денежность» против «липкого страйка».
Больше всего смущает то, что в работе Блэка и Шолеса, на которую постоянно ссылаются оппоненты, нет вообще никаких упоминаний о «кривой волатильности», волатильность у БШ есть константа. Чем «кривее» кривая IV для конкретного рынка, тем меньше модель БШ подходит для его описания, это вся информация, которую кривая IV в себе содержит.
Спор о том, следует ли учитывать ее наклон при вычислении дельты, подобен спору о количестве чертей, способных уместиться на острие иголки. Мне кажется, правильнее изменить модель БШ, чем стараться подогнать ее неверные результаты под реальные рынки.
Напомню об одном из возможных подходов к такой модификации.
1. Собираем статистику — набор исторических пар {d(Fut),d(ImpVol)};
Где d(Fut) – дневное приращение БА
d(ImpVol) – приращение волатильности опционов на центральном страйке за тот же день.
Строим диаграмму приращений, получится что-то вроде того, что на рисунке 1
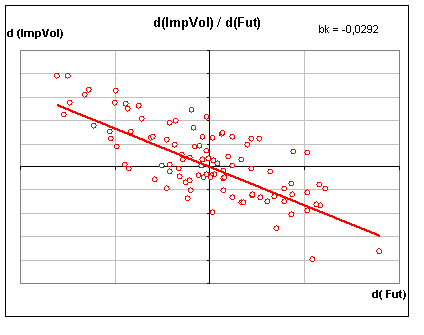
Рис.1
Простой взгляд на картинку подводит к мысли о том, что волатильность можно представить линейной функцией цены базового актива. Исходя из этого, положим σ(F)=a+bF, где F – стоимость БА; a,b – некоторые константы, которые подбираются для конкретного рынка.
2. Идем к уравнению в частных производных, которое решали БШ.
В соответствии с предположением заменяем σ2 на (a+bF)2 .
3. Решаем полученное уравнение и получаем новые соотношения для справедливой цены опциона.
4. Пробуем с их помощью описать реальные рынки. Подбираем параметр a (он определяет высоту центральной точки), затем параметры bp,bc по отдельности для ветвей Call, Put (они определяют кривизну ветвей). Получится так, как на рис.2
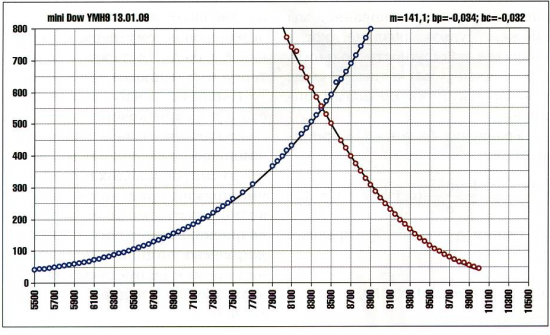
Рис.2
Все. Никакая кривая IV не понадобилась. Если полученная точность не устраивает, выберите другую зависимость σ(F), или σ(F,t). Или, если полагаете, что коэффициент наклона b не константа, а случайная величина, рассмотрите стохастическое уравнение. Это все вполне решаемые задачи. Во всяком случае, вопрос о том, как правильно посчитать дельту, отпадет сам собой.
PS. Я не привожу здесь свои формулы. При их выводе в качестве меры активности БА использовалась не волатильность, а подвижность. Они хоть и связаны друг с другом взаимно-однозначным соответствием, но нелинейным, поэтому получить из одной формулы другую просто так не получится, а решать все заново не хочется.























Ну… ночером в массах подобное и вообще вне восприятия
Ваш подход очень близок к моему. Если бы я опцики исследовал, примерно также бы начал.
не все ;)
Со временем становятся заметными неслучайние составляющие. Поэтому и спрашивал об изменении представлений с годами и об отношениях с новомодными.
Насколько я понимаю, в формуле БШ и не должно быть IV — это же видение волатильности рынком. Собственно успешность опционной торговли и определяется умением правильно рассчитать волатильность, чтобы подставить её в формулу. Рынок почти всегда видит её не правильно.
Кто тут теоретик, а кто практик, думаю, Вы уже поняли.
Но если не нравится линейная функция, рассмотрите другую. В любом случае учет зависимости Vol(БА) улучшит результат и распрямит кривую IV
Если каким либо методом оценивать HV, результат будет зависеть от длины временного окна. Мы все это знаем, но чисто эмпирически берем какой-то метод расчета и какой-то определенный параметр усреднения. В некотором роде здесь то же самое. Аналогия удаления по страйку от центра и увеличению окна при расчете HV, мне представляется, существует.
вы не сможете описать к примеру вот это:
Для статистики нужна волатильность только центрального страйка, это одна точка.
Извините, но действительно не могу понять вопроса. Попробуйте без термина «skew».
Если вопрос о том, можно ли одним набором параметров описать все рынки, то, разумеется, нет. Для каждого рынка свой набор.
PS. И что у mini Dow нет улыбки?
а вот это биржа просто ради себя придумывает...https://www.moex.com/a186
дельта дальше считается элементарно
а так — кто какую модель «прочувствовал», тому такая и удобней...
как говорится -прочувствовал, -под себя подогнал, -профит!
PS: автор, вы же кажется давно уже подвижностью занимаетесь, какой месячной доходности в снеднем удается по опционам достичь, если не секрет?
а интересно как оно там нынче, в быту))
В общепринятой методики делают точно так же. Только функцию нашей добавочки строят отдельно. Берут корреляцию БА/волатильность (наклон улыбки). Расхождение распределения БА с нормальным стандартным распределением загиб улыбки. И у нас получается гладкая квадратичная функция описывающая и дельту и время и все процессы. Она содержательна и наблюдаемая. Конечно, эту функцию можно вставить непосредственно в БШ. Тогда к сигме надо прибавить разницу между ЦС и волой на кривой волатильности. Но, обычно, это делают отдельно и сразу ставят в формулу сигму с улыбки. Ну и естественно ваша улыбка не обязана лежать на бидах асках, у вас может быть свой взгляд и своя улыбка.
Насколько понял, Вы в своей модели исходите из того же предположения, что и в модели БШ: торговля ведется непрерывно и без гэпов. И поэтому предполагаете, что PnL позы с опционом можно полностью повторить с помощью голого БА. Т.е. возможна «безрисковая хеджированная позиция». Например, продажа колла и покупка БА, в которой прибыль/убыток по опциону точно компенсируется убытком/прибылью по БА.
Но нет ли тут ошибки? Ведь в реале торговля прерывается и есть гэпы. Если у нас есть проданный опцион и не повезло попасть на гэп, то хеджирование с помощью БА будет запоздалым и не покроет одномоментно полученный убыток по опциону.
Проблема ведь не только в гэпах (одномоментных больших приращениях). На них просто особенно четко видно, что повторить с помощью линейного БА нелинейное поведение опциона — не получится. Но ведь и на средних приращениях — тоже самое. Реакция с хеджем будет запоздалой. Движение цены БА уже произошло, опцион уже принес какой-то PnL, а мы только после этого совершаем сделку с БА, по новой цене. Т.е. будет идти постоянное отставание хеджирующей позиции с БА от исходной с опционом.
Или в идее с безрисковым портфелем считается, что хеджирующую сделку с БА мы совершим не после движения, а перед ним? Т.е. как будто умеем предсказывать каждое приращение, и можем заранее совершить сделку с БА, чтобы точно воспроизвести опцион (диаметрально противоположный исходному, который хеджируем)?
А как относитесь к подходу через сценарное планирование? Т.е. выделяем несколько возможных сценариев, каждому назначаем вероятность, прорабатываем каждый сценарий в отдельности (строим для него распределение вероятностей, где будет цена БА на экспу если реализуется именно этот сценарий), делаем смесь этих распределений (вес каждого = вероятность сценария) и получаем итоговое распределение вероятностей, по которому уже можно считать цены опционов (через матожидание выплат). При таком подходе ведь все можно учесть: и гэпы, и взлет страха на пустом месте (рост IV при стоящем БА), и другие моменты, которые подход через «безрисковый портфель» не может отработать.
Сценарный анализ вещь замечательная, проблема лишь в том, откуда брать для них вероятности. Обычно берут с потолка, поэтому результаты очень сомнительные.
(рыночное распределение — тонкая линия, смесь 3х нормальных — сплошным серым)
Т.е. как-бы рынок своими ценами подразумевает:
1. С вероятностью 60% будет случайное блуждание начиная с текущих 118000 с сигмой 2800п (что эквивалентно примерно 15% воле).
2. С вероятностью 20% будет падение в район 114000.
3. С вероятностью 20% будет рост до 121500.
И «расшифровав» так рыночные цены в физически понятные цифры (а не в абстрактные подгоночные коэф-ты), уже можно осознано вступать в спор с рынком, если есть уверенность, что вероятности каких-то сценариев недооценены/переоценены или в них неправильные мю/сигма.
Как такая идея?
imo, единственное эффективное занятие — их изучение и прогнозирование, от тиков до месяцев.
У себя сделал Советник, который по заданному распределению вероятностей и отношению к риску ищет оптимальную позицию. Так вот, если дать даже 0.0...01 вероятность на краевой сценарий и использовать ф-цию полезности с неприятием риска, то Советник никогда не предложит позу с голым проданным краем. Всегда находится поза с более лучшими показателями и с ограниченным убытком.
Так что, думаю, «черные сценарии» — это не такая уж и проблема.
если взять сценарный подход (как пример парой комментов ниже, из трех сценариев: с вероятностью 60% — случ.блуждание, 20% — падение, 20% — рост), то у нас получается смесь из нескольких случайных процессов. Правильно ли понимаю, что в Вашей терминологии такую смесь уже нельзя назвать случайным процессом, а надо называть неопределенным процессом?
Условный пример: если наши перебрасывают войска в Венесуэлу -> эскалация с США -> новые санкции -> отключенный swift -> реализуется сценарий падения Ri. И случайности тут никакой нет, а есть в данный момент неопределенность: примут решение о переброски войск или нет. А случайности начнутся потом, как именно колбасить будет после падения.
Вот поэтому различаете случайность и неопределенность?
Очень жаль, что Вы не поместили тему в спецраздел «Опционы» — поэтому её пропустил.
Понятно, что основные баталии уже отгремели, но все же попробую продолжить разговор.
1. Вы нарисовали цены путов и колов. Замечательно.
В теле поста на одном графике есть цены близкие к 0 и есть цены близкие к 800.
В комментарии есть цены близкие к 0 и есть цены близкие к $30.
Это банально неудобно для визуального восприятия.
Поэтому следующим шагом абсолютные цены нужно привести в стандарное представление. Что для этого делаем? Правильно: для каждой цены вычисляем ее волатильность с использованием формулы Блека-Шолза.
Подчеркиваю: мы НЕ используем теорию БШ. Но мы используем их ФОРМУЛУ для превращения абсолютных цен в айви.
Хочется увидеть получившийся график (точнее, их должно быть 2: один для путов и один для колов).
2. Вы начали разговор про дельту, а остановились на вычислении цен опционов.
Итак, цены опционов у нас теперь есть (точнее, они у Вас есть).
Теперь их надо продифференцировать по dF. Что получается?
С уважением.