Информация
Блог им. jamebonds
Про мартингейл (ликбез)
- 14 июля 2017, 20:56
- |
Просто удивительно, какой процент участников смартлаба (см. опрос) считает, что мартингейлом можно получить прибыль.
Играем в бросание монетки. Орел = + 1 рубль, решка -1 рубль. Комиссии, спреды, свопы/контанго не учитываем.
Будем бросать 4 раза подряд. Сначала играем без мартингейла.
Рассмотрим сразу все возможные исходы партий.
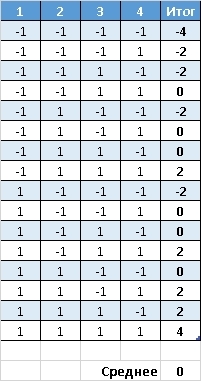
Отметим, что средний итог всех партий = 0.
По всем возможным исходам построим гистограмму, где на горизонтальной оси будет итог партии, а на вертикальной оси будет количество партий, приводящих к такому итогу.
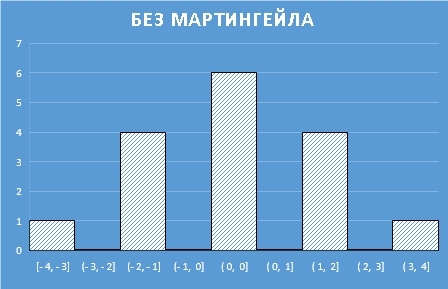
Как видно, плотность вероятности симметрична и максимум у нее на 0.
В переводе на обывательский язык это означает, что, применяя такую систему, скорее всего вы будете на 0.
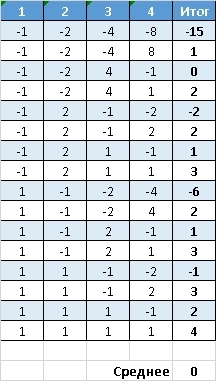
Теперь сыграем с мартингейлом. Также рассматриваем сразу все исходы.
И строим гистограмму.
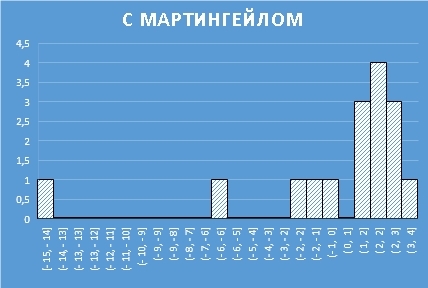
Отличия от игры без мартингейла есть: теперь наиболее вероятный итог партии +2 рубля. Но гистограмма стала не симметричной, у нее появился хвост в области отрицательного исхода.
Отметим также, что средний итог всех партий опять равен 0 !
Опять переведем на обывательский язык: скорее всего, вы будете в плюсе, если не разоритесь.
Чем больше количество бросков в партии, тем больше будет расти у вас этот хвост плотности вероятности. Это означает рост вероятности полного разорения.
Поэтому мартингейл для трейдера невыгоден: Мартингейл повышает вероятность полной потери капитала, но не изменяет вероятности выигрыша (мат. ожидания прибыли/убытков).
Нет смысла повышать себе риск полного разорения.
Обыватели, забывающие про хвост плотности вероятности и упрощающие фразу до "скорее всего вы будете в плюсе" разоряются в трейдинге.
Вопрос к залу: какой математической величиной описывается данная характеристика плотности вероятности? Пишем в комментариях.
Всем, кто еще не читал настоятельно рекомендую: Ральф Винс «математика управления капиталом». Цитирую по памяти: «Никакие способы управления капиталом (т.е. величиной позиции) не способны сделать из убыточной стратегии прибыльную.» Это относится и к Мартингейлу и к другим системам (Лебушер, например).
теги блога Jame Bonds
- amp clearing
- Brent
- CME
- ducascopy
- exante
- FORTS
- gold
- interactive brokers
- MetaTrader 5
- metatrader5
- Ninja trader
- o-s-a.net
- roundtrip
- RTS
- saxo
- Si
- алгоритм
- банки
- биржа сломалась
- биржи США
- БКС
- брокер
- брокеры
- бэквордация
- валютный рынок
- Вечерняя сессия
- Возврат налога
- вопрос
- вранье достало
- ГО
- денег нет
- Дипломатия
- Доллар рубль
- еврооблигации
- золото
- квалифицированный инвестор
- клиринг
- комиссии
- контанго
- контанго и бэквордация
- куда бежать
- кухня
- ликбез
- мартингейл
- мир
- ММВБ
- МосБиржа
- Московская биржа
- налогообложение на рынке ценных бумаг
- НАТО
- НДФЛ
- нефть
- новый год
- опрос
- опционы
- открытие
- Открытие брокер
- оффтоп
- охренели
- ошибки
- Палладий
- перелив
- перелив счета
- переход
- планка
- Планки
- платина
- плохо
- политика
- проп
- расписание
- расписание торгов
- раундтрип
- реклама
- РФ VS сша
- сайт
- санкции
- Сбербанк
- сбор за неэффективные транзакции
- сервер
- Серебро
- Сирия
- сопля
- СПБ биржа
- срочный рынок
- страхование
- теория
- Технические проблемы
- торговые роботы
- торговый софт
- трейдинг
- Финам
- фондовый рынок
- ФОРТС
- фьючерс
- фьючерсы
- хана
- экспирация
- юмор
- Янки
Если вы считаете, что я не прав, приведите пример.
Однако противоречия я не вижу: мат ожидание одинаково, что с усреднением, что без. Это и показано в посте ;).
soer, а Вы не стесняйтесь. Поразите нас своим интеллектом и крутыми математическими терминами.
Тут не все имеют 3 класса церковно-приходской школы.
LogikoMen, нет. Без разницы сколько раз выпал орел. Вероятность следующей решки остается 0.5.
Ну, по крайней мере в идеальном математическом мире.
LogikoMen, не понял Ваш вопрос.
Если события независимы между собой, то какая бы невероятноя цепочка не случилась только что, обо всем этом можно сразу забыть. Вся математика ровно такая, как если бы никакой предыстории не было.
Ещё раз повторюсь: в идеальном математическом мире бросков идеальных монет без памяти.
При этом рынок скорее всего имеет некую память, страдает от неэффективностей различного вида и вся наша работа алготрейдера — это найти те ситуации, в которых монета становится несимметричной (либо по вероятности, либо по выигрышу, либо одновременно).
В нашей же беседе есть непонимание. Я говорю об возврате отклонения в серии бросков. А вы об одном. Один бросок — это статистическая единица. На которой еще ни один трейдер не пытался заработать. И я не подвергаю сомнению правило, которое все знают. Но тем не менее мартингейл ориентирован на серию. А не один бросок. И так во всем. Любой шанс в теории вероятности можно эксплоатировать. Но это возможно на серии. На одном исходи — утопия и абсурд.
LogikoMen, понятно. Вы (как и многие) считаете, что из равновероятности выпадения орла/решки следует, что кумулятивная сумма будет болтаться около нуля.
Это грубая ошибка. Никакой «возвратности к нулю» у кумулятивной суммы нет.
Всем успехов ;)
я всё хочу как-нибудь попробовать запрограммить антимартингейл — чтоб уменьшать позу при неугаде. и увеличивать при угаде — ставим на то, что настоящая случайная монета часто делает повторы.
напишу здесь чтоб не забыть. всего пару строк но щас лениво :)
Это — схема Бернулли. Можно сосчитать матожидание длин серий. Оно равно 2. Казалось бы — вот оно! Однако количество серий длины 1 равно в сумме количеству всех серий длины >1.
Всё это следствия выделенного ниже:
Каждое новое испытание имеет вероятность 1/2 вне зависимости от исхода предыдущего.
не понимаю как люди применяют математику частично
вроде уже общеизвестно, что при очень большом количество бросков монеты, результат будет очень далек от нуля.
вторая ошибка — принципиальная. никто не мартингейлится равномерно.
а значит не будет такого результат как вы изобразили.
Vanuta, а потом Трансаэро оказывается банкротом.
Ни одна схема мартингейла этот исход не учитывает.
При очень большом количестве бросков монеты результат с максимальной вероятностью — это 0. Это строго доказуемо.
При этом вероятность результата «очень далеко от 0» может быть выше, чем результата «0». Это не противоречие, потому что «очень далеко от 0» включает в себя результаты от -бесконечность до -X и от Х до +бесконечность, где Х — ваше понимание «очень далеко».
(Симулятор-калькулятор убыточных трейдов подряд...)
Эксель 2003 >>>
Эксель 2010 >>>
DeltaZero, эта картинка — расчет числа Пи методом Монте-Карло.
К обсуждаемой задаче отношение не имеет. Не надо вводить коллег в заблуждение. =) Мы и сами заблудимся.
Вот торговали ребята мартингейл. 1 месяц +500%, 2-ой месяц — около 0, еще 2 месяца и -50%.
Проблема всё таки в ограничении депозита, если он бесконечен мартингейл выигрывает всегда.