SMART-LAB
Новый дизайн
Мы делаем деньги на бирже
Блог им. RazInv
Облигации. Изменение цены при росте доходности
- 13 октября 2020, 10:58
- |
На Смарт-Лабе возник спор между двумя уважаемыми авторами (и частично между их комментаторами) по поводу того, насколько изменится цена облигации, если у нее была доходность 0,5%, а на рынок выйдут облигации с доходностью 4%
Я не буду выбирать ни чью сторону в этом споре, но хочу внести некоторую ясность в процесс ценообразования. Желающие могут найти тонны литературы по грамотному расчету ценообразования и доходностей облигаций, я лишь приведу простой пример на основе данных, предложенных в споре
Когда идет речь о доходностях акций, то все достаточно просто, т.к. на акции выплачивается фиксированный в рублях дивиденд. Например, по акции будет выплачено 10 руб. дивиденда. Тогда если при таком дивиденде доходность составляет 0,5%, то цена акции должна быть 10/0,005 = 2 000 руб., чтобы доходность выросла до 4%, цена должна упасть до 10/0,04 = 250 руб. Все просто
Но с облигациями все немного сложнее. Для простоты примера и расчета я возьму условную облигацию с номиналом 1 000 руб., со сроком до погашения 2 года, выплатой купонов два раза в год и доходностью к номиналу в 7% (таким образом, раз в полгода будут платиться 35 руб. купонов) — этакая эталонная облигация. Какова будет цена облигации при разной требуемой доходности (в споре 0,5% и 4% соответственно)?
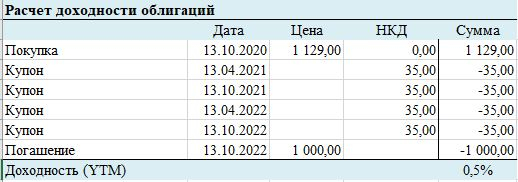
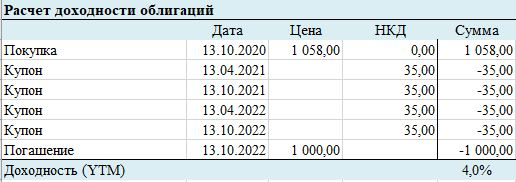
Для конкретной данной облигации ситуация выглядит таким образом — чтобы ее доходность выросла до нового рыночного уровня в 4% ее цена должна снизится с 1 129 руб. до 1 058 руб., т.е. на 6,3%
Я хотел показать без лишних теоретизирований, лишних формул и сложных объяснений, как это выглядит в реальности. Один из авторов просил показать конкретные цифры, я полагаю, что данный пример позволит наглядно показать процесс изменения цены облигаций для подстройки к изменяющейся рыночной доходности
Я не буду выбирать ни чью сторону в этом споре, но хочу внести некоторую ясность в процесс ценообразования. Желающие могут найти тонны литературы по грамотному расчету ценообразования и доходностей облигаций, я лишь приведу простой пример на основе данных, предложенных в споре
Когда идет речь о доходностях акций, то все достаточно просто, т.к. на акции выплачивается фиксированный в рублях дивиденд. Например, по акции будет выплачено 10 руб. дивиденда. Тогда если при таком дивиденде доходность составляет 0,5%, то цена акции должна быть 10/0,005 = 2 000 руб., чтобы доходность выросла до 4%, цена должна упасть до 10/0,04 = 250 руб. Все просто
Но с облигациями все немного сложнее. Для простоты примера и расчета я возьму условную облигацию с номиналом 1 000 руб., со сроком до погашения 2 года, выплатой купонов два раза в год и доходностью к номиналу в 7% (таким образом, раз в полгода будут платиться 35 руб. купонов) — этакая эталонная облигация. Какова будет цена облигации при разной требуемой доходности (в споре 0,5% и 4% соответственно)?


Для конкретной данной облигации ситуация выглядит таким образом — чтобы ее доходность выросла до нового рыночного уровня в 4% ее цена должна снизится с 1 129 руб. до 1 058 руб., т.е. на 6,3%
Я хотел показать без лишних теоретизирований, лишних формул и сложных объяснений, как это выглядит в реальности. Один из авторов просил показать конкретные цифры, я полагаю, что данный пример позволит наглядно показать процесс изменения цены облигаций для подстройки к изменяющейся рыночной доходности
3.8К |
Читайте на SMART-LAB:

Снижение военной премии в нефти: что это меняет для доллара и G10
Во второй половине понедельника – начале вторники рынки активно пересматривают премию за худший сценарий на энергетическом рынке, что цепочкой...
16:32

12 марта Группа Ренессанс страхование опубликует МСФО за 2025 год
Напоминаем, что 12 марта 2026 года RENI опубликует МСФО Группы за 2025 год, а также проведет День инвестора, чтобы рассказать о ситуации на...
13:40
теги блога ИнвестБродяга
- ebitda
- FIRE
- IPO
- ROE
- SPO
- акции
- акции роста
- Алроса
- аналитика
- Астра
- банки
- все инструменты
- ВТБ
- Газпром
- горнодобывающая отрасль
- Делимобиль
- Джетленд (JetLend)
- Диасофт
- дивиденды
- долгосрочное инвестирование
- дом.рф
- допэмиссия
- доходности облигаций
- дробление
- Европлан
- ЕвроТранс
- займер
- золото
- идея
- иис
- инвестиции
- инвесторы
- Интер РАО
- интеррао
- капитал
- капитализация
- Кармани
- конвертация
- кубышка
- Ленэнерго
- ленэнерго ап
- металлургия
- Минэнерго РФ
- ММК
- МосБиржа
- Московская биржа
- мсфо
- МТС банк
- мультипликаторы
- нлмк
- Новатэк
- Облигации
- отчетность
- офз
- падение
- первичное размещение
- первичное размещение акций
- Полюс Золото
- преимущественное право
- привилегированные акции
- прогноз
- прогноз по акциям
- размещение
- ранняя пенсия
- Ренессанс
- рентабельность
- риск
- Риски
- Россети
- Россети Волга
- россети ленэнерго
- Россети Центр
- Россети Центр и Приволжье
- Российский рынок
- Ростелеком
- РСБУ
- Русагро
- рынок
- Сбербанк
- Северсталь
- Сети
- совкомбанк
- Совкомфлот
- сплит
- ставка ЦБ
- сталь
- стоимость
- трейдинг
- форум
- ФСК Россети
- ЦБ
- цветная металлургия
- чистая прибыль
- Чёрная металлургия
- Швагер
- электроэнергетика
- Элемент
- энергетика
- ЮГК
- Юнипро





















Именно про дюрацию никто ничего из спорящих не написал… И вы, решив стать судьей, забыли про неё.
ВОт потому и мимо
блин… да кому здесь это нужно -)) Ок...
КРЫС, мне это нужно. Если я ошибаюсь, то хочу разобраться в чем именно. Или вы говорите про теорию — как именно изменяется цена облигации в случае изменения требуемой доходности в зависимости от дюрации данной облигации? Я просто в конкретном посте не хотел писать теорию, я хотел, чтоб «все было просто».
Если же про математику — то я пересчитал свой расчет в комментарии ниже с учетом «бессрочности» своей указанной в посте облигации: (номинал 1 000 руб., купоны два раза в год, ставка купона к номиналу 7%, но срок — бессрочный) цена облигации при доходности в 0,5% будет
70 / (2*((1+0,005)^(1/2)-1)) = 14 017. При доходности в 4% цена будет 1 767, т.е. падение цены в 7,93х (ну или в 8 раз)
На самом деле тут все от лукавого... Цифрами можно поиграться как хотите… Никто не запрещает брать изначально очень высокую/низкую цену, очень низкую/высокую рыночную ставку. Можно получить различные цифры. Но в реальности же все происходит не так.
Вы взяли очень консервативный пример. Я бы рекомендовал взять или реальную американскую тридцатилетку, или нашу 26230… И вот уже с ними побаловаться...
при доходности 0,5% цена 2 145 руб.
при доходности 4,0% цена 1 397 руб.
таким образом для данной реальной облигации с теоретическими уровнями доходности получаем, что при росте доходности в 8 раз с 0,5% до 4% ее цена снизится на (2 145 — 1 397) / 2 145 = 34,9% (почти как в приблизительном расчете через мод.дюрацию)
при доходности 0,5% цена 2 145 руб.
при доходности 4,0% цена 1 397 руб.???
более дорогая облигация приносит меньшую доходность?
и еще, у Вас в рисунках напротив Доходности стоит аббревиатура YTM, она ведь расшифровывается как Эффективная доходность к погашению!!!
вот тут я и не понимаю логики! )
зачем мне покупать дорогую бумагу, которая приносит меньше доходности??
Я же говорю, что в обоих случаях это одна и та же облигация. Но разные требуемые доходности / ставки на рынке. То есть речь не идет о том, что она одновременно дает доходность и 0,5% и 4%. Когда на рынке ставки 0,5%, то и цена на эту облигацию «высока» и ее доходность 0,5%. Когда на рынке ставки 4%, то и цена на эту облигацию «низкая» и ее доходность 4% (в реальности же ее цена не «высокая / низкая», а такая, что отражает текущие требуемые рыночные доходности). Т.е. эти цены — они в разные периоды времени при разных условиях
70 / (2*((1+0,005)^(1/2)-1)) = 14 017. При доходности в 4% цена будет 1 767, т.е. падение цены в 7,93х (ну или в 8 раз)
Нет :) Акция — это доля бизнеса. Вы можете конечно хотеть любую доходность, но на практике есть акции и с 10+% дивов, и без них вообще, и первая может падать, а вторая расти. Доходность вложения не зависит только от дивидендов, т.к. есть курсовая стоимость.
Поздравляю, вы открыли дюрацию :) У двухлетки с купоном она ниже 2-х лет, поэтому и при поднятии ставки на 3,5 п.п. цена тела падает менее чем на 7 п.п. Считают именно в п.п., никаких кратных приростов доходностей там нет в реальности.
Бессрочные облигации точно так же считать нельзя, хотя бы по одной причине (не считая бесконечного срока) — у бессрочной нет тела по факту, т.к. его никто не обещает вернуть. Примерно как у префов.
Тем не менее, у них тоже есть дюрация :) Посмотрите на реальные бонды того же РСХБ, их рынок прайсит около 8% (они вроде суборды + бессрочка + корпорат с ндфл, так что неплохо относительно офз), для примера возьмём размещения по 9 и 14% (я округляю).
У 9%-х (2018) дюрация 5,5, соответственно при поднятии ставки и прайсе 8% годовых мы получили +5,5% тела. Они торгуются по 105,88.
У 14%-х (2016) дюрация 4,5, но они тоже оценены в 8%, разница 6 п.п., т.о. рост тела на 27%. Торгуются по 127,4.
Я сильно округлял, но принцип думаю понятен. Плюс есть и другие факторы, но для топорных расчётов дюрация * разницу ставки в п.п. вполне можно использовать.
1. Относительно акций — этот пример я привел лишь для того, чтобы показать, что при фиксированном дивиденде (в руб.) изменение доходности обратно пропорционально изменению цены акции
2. Относительно облигаций — да, я в курсе про дюрацию :) но я не хотел про нее писать. Цель поста была в том, чтобы максимально просто показать, что при изменении требуемой доходности изменение цен на акции кардинально отличается от изменения цен на облигации. При этом я понимаю, что у облигаций изменение цен приблизительно равно изменению доходности (малому приращению), умноженному на мод.дюрацию со знаком «минус». Я там выше в комментарии по совету коллеги КРЫС посчитал изменение по реальной ОФЗ 26230, у нее при росте доходности с 0,5% до 4% (как в споре) цена упадет на 34,9%
3. Относительно бессрочных облигаций — да, я понимаю, что для ее расчета используются несколько иные формулы. Я там тоже в комментарии выше приводил расчет — вот такой «для моего примера (номинал 1 000 руб., купоны два раза в год, ставка купона к номиналу 7%, но срок — бессрочный) цена облигации при доходности в 0,5% будет
70 / (2*((1+0,005)^(1/2)-1)) = 14 017. При доходности в 4% цена будет 1 767, т.е. падение цены в 7,93х (ну или в 8 раз)»
4. Относительно реальных «вечных» облигаций РСХБ — пойду поизучаю их, спасибо за направление
Грубо говоря, имея 7% купон и неизвестное время возврата тела, можно предположить, что дюрация будет 13-14 максимум (дюрация — это «срок возврата вложений», за 13 лет тело вернётся купонами). Меняя ставку на 3,5 п.п. мы двинем тело пунктов на 50 скорее всего. И то вряд ли — измерение скорее всего не линейно на больших движениях ставки. Плюс спрос упадёт по пути. При неизменном купоне и сроке и выросшем теле вырастет и дюрация, и соответственно риски для инвесторов.
Также посмотрите кривую доходности ОФЗ — во-первых, после 10+ лет премия за срок подозрительно уравнивается, видимо и 10, и 20 лет прайсят примерно одинаково, т.е. нет никакой линейной экстраполяции типа в 10 раз дольше — в 10 раз дороже. Во-вторых, чем больше срок, тем сильнее дюрация отличается от этого срока. У 18-летки дюрация 10, у 15-летки — 9.
С нашими космическими купонами сложно себе представить дюрацию больше :) Для западных купонов можно точно так же посмотреть примеры, причём у них ещё и 30-летки есть. Я просто ими не торгую, поэтому не вникал. Но есть, к примеру, наши евробонды чуть ли не из 90-х, которые когда-то эмитировались с купонами по 10+%. Сейчас долларовая ставка внизу, но по 400-500% они не торгуются :) И никогда не торговались.
1. Я рассчитал доходность бессрочной облигации, применив формулу расчета вечного аннуитета (ренты) с учетом выплат купонов два раза в год. Видимо, в данном случае брать эту чистую формулу не совсем корректно (и даже ошибочно) — там, конечно же, погашение тела не учитывается вообще никак (его просто нет)
2. Относительно дюрации бессрочной облигации — при купоне 7%, выплате купонов 2 раза в год, покупке ее 14.10.2020 и отсутствии срока погашения у меня по расчетам получается, что ее дюрация равна 14,71 лет. Мод.дюрация соответственно 13,74 лет. Соответственно при линейном изменении цены облигации к изменению доходности получается так
Дельта Р = — мод.дюрация * дельта доходности = -13,74 * 0,035 = -48%, т.е. падение цены облигации составит 48% — я корректно считаю?
Однако я понимаю, что подобная формула применима в первом приближении лишь при малых изменениях ставки (а тут ставка меняется с 0,5% до 4%, что вряд ли можно считать «малым»), Но в целом вроде как-то так получается
3. Про линейную зависимость у длинных ОФЗ ясно, это я понимаю
4. Про наши сверхдолгие долларовые еврооблигации из 90-х — это интересно, посмотрю на их цены и их изменение
Вариант с 0,5:
я получаю деньгами в конце двух лет 1000+35•4=1140
отдаю сейчас 1129, тогда профит 11 р.
значит сейчас для меня 11/1129 и еще раз на 1/2 и на 100%
ну и получаю свою доходность 0,487156%
второй пример аналогично.
так не правильно считать?
Именно поэтому я привел в табличке даты поступления купонов и погашения основной суммы долга — все эти деньги необходимо привести к текущей дате. Для простоты это делается в Excel с помощью функции ЧИСТВНДОХ() — эта функция рассчитывает ставку дисконтрования. В данном конкретном случае она высчитывает доходность к погашению указанных облигаций