SMART-LAB
Новый дизайн
Мы делаем деньги на бирже
Блог им. Kot_Begemot
Авторегрессия волатильности как задача для стохастического градиентного спуска.
- 10 сентября 2019, 18:45
- |
Занимаясь первоначально исключительно портфельным инвестированием мы всё чаще сталкиваемся с задачей моделирования волатильности фондового рынка и его будущих ковариаций. Соответственно, так или иначе, мы сталкиваемся с проблемой выбора модели, которая позволяла бы нам на самом широком диапазоне данных получать сколько-нибудь значимые оценки.
В качестве показателя качества моделей нами была выбрана доля объяснённой дисперсии:
и промоделирована ошибка измерения волатильности заданного стационарного процесса на интересующем нас интервале:
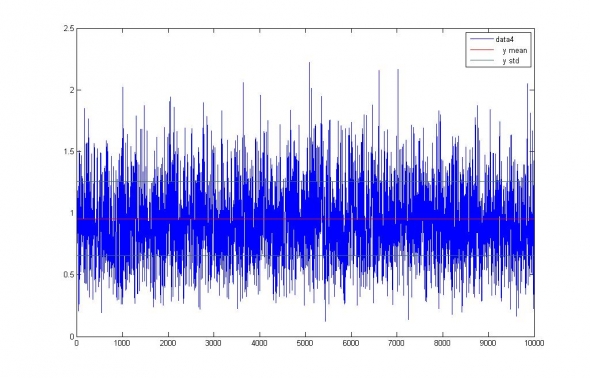
Рис.1. Измерение волатильности белого шума ~ N(0,1) на 5-и дневном интервале.
Среднеквадратичная ошибка измерения волатильности составила 0.3 = 30% от собственной волатильности шума. А прогностическая модель IV=1, то есть лучшая из всех возможных моделей, пользующаяся априорно известными данными, показала уровень качества 0.9. Таким образом, мы получили оценку максимально возможной точности прогноза волатильности на период недельного интервала.
Для тестирования спектра моделей были выбраны акции ПАО Газпром и ПАО Сбербанк историей за 10 лет (Is выборка), в предположении покупки недельных опционов (5 дневная «OoS» выборка), по известной годовой предыстории (240 дневная выборка).
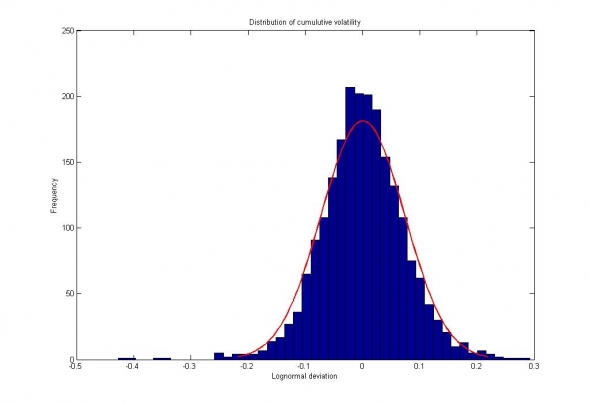
Рис. 2. Сбербанк. Распределение приращений цен за недельный интервал, представленное слабовыраженным распределением с «тяжелыми хвостами».
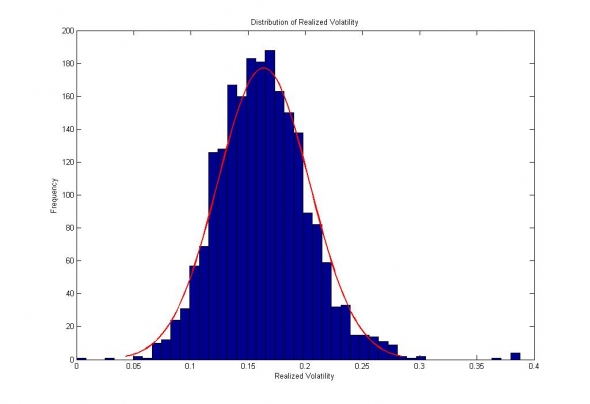
Рис.3. Сбербанк. Распределение измеренной волатильности внутри недельных интервалов.
В качестве авторегрессионных моделей волатильности мы взяли :
- Simple Moving Average
- SVD-SSA
- GARCH(1,0)
- ARCH(240)
- +некоторые другие
Как ни странно, наилучшими результатами отличились стандартные ARCH и GARCH модели :
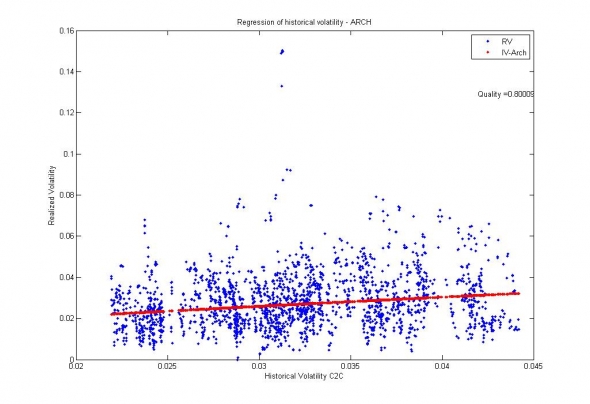
Рис. 4. Сбербанк. Обобщение данных GARCH(1,0) моделью. Доля объяснённой дисперсии = 0.8.
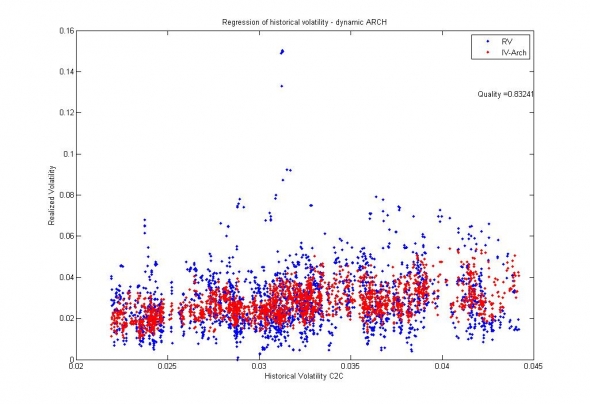
Рис. 5. Сбербанк. Обобщение данных АRCH(0,240) моделью. Доля объясненной дисперсии = 0.83;
Соответственно, с учётом предельной точности моделей 0.9, можно говорить о том, что ARCH и GARCH модели волатильности по отношению к рынку являются исчерпывающими, а их коэффициенты — стационарными, достаточными для того, чтобы можно было строить глобальные статистические модели, методом стохастического градиентного спуска.
3.3К |
Читайте на SMART-LAB:

📅 Как работают торги в выходные
В 2026 году на бирже пройдёт 52 сессии выходного дня, в том числе и по праздникам — 23 февраля, 1 мая, 12 июня, 4 ноября. Что и когда...
15:03

Банк России и ФАС запретили банкам навязывать конкретных страховщиков при выдаче кредитов
Отличные новости для независимых страховых, как RENI! Сегодня стало известно, что ЦБ и ФАС направили совместное письмо банкам, которое...
13:06
теги блога Kot_Begemot
- API
- cpp
- FORTS
- LUA
- Matlab
- NASDAQ
- open source
- Quik Lua
- S&P
- S&P500
- S&P500 фьючерс
- Vanguard Group
- VIX
- акции
- акции США
- алгоритмы
- алготрейдинг
- анализ временных рядов
- баффет
- волатильность
- Гордон
- доверительное управление
- долги
- игры
- инвестиции
- индекc
- интеграция
- искусственный интеллект
- Келли
- Книги
- книги о трейдинге
- корреляция
- кризис
- криптовалюта
- лудомания
- Марковиц
- матлаб
- машинное обучение
- ММВБ Акции
- наука
- нейронные сети
- облигации
- одураченные случайностью
- оптимизация
- оптимизация торговых систем
- опционы
- оффтоп
- оционы
- памм счета инвестиции
- паника
- пирамида
- ПИФы
- портфели
- Портфель
- портфельное инвестирование
- пузыри
- раздача
- рецензия
- Риски
- рэнкинг мосбиржи
- Сбербанк
- спекуляции
- статистика
- стоимостное инвестирование
- талеб
- теги не нужны
- теория игр
- торговая система
- торговые роботы
- трейдинг
- улыбка волатильности
- управляющая компания
- финанализ
- фундаментальный анализ
- фьючерс ртс
- Шарп
- шутка
- Экономика





















От винта! Подбирать порядок модели это уже отдельная задача. 240 — это достаточно много чтобы набрать статистику и мало-ли, вдруг там сезонность появится? Глазом-то она вроде бы и есть (из-за сглаживания линейным фильтром оценок дисперсии), но SSA её не ловит (точнее ловит, но в убыток).
Да, но в разных композициях она превращается в подвид GARCH и работает очень даже не плохо. Собственно, GARCH у меня так и построен.
Нет. Но, быть может, попробую. Пока у меня есть сомнения на счёт EWMA и подобных взвешиваний ряда. Время от времени он угадывает, но чтобы по всем рядам и рынкам его гонять — тут проблема.
Eugene Logunov, нужно очень четко понимать почему используется та или иная формула. А то можно обмануться дорого. Да, СМА гавкает дважды, но зато она меряет то, что должна мерять — второй центральный момент распределения.
А что померяет ЕМА? Меряет ли она второй момент? Будет ли оценка смещенной? Какая у неё будет дисперсия?
Eugene Logunov, звучит уверенно, но не убедительно.
С уважением и благодарностью.
А если у вас какой-то процесс с памятью, какой-нибудь switch процесс, вроде HMM и тому подобное, то смещением будет обладать уже обычная оценка, увязшая в уже «поломанных» статистиках.
Если волатильность подчиняется трендам… (её АКФ(1)>0), переходит из состояния в состояние (АКФ(1)>0) или, например, представляет из себя некоторое броуновское движение (АКФ(1)>0), то ЕМА просто обязана обладать меньшим смещением.
Kot_Begemot, в предельном переходе к обычному броуновскому блужданию индикатор волатильности должен с высокой точностью показывать истинную волатильность этого процесса.
Если ЕМА этим свойством не обладает (а вдруг?), то на мой взгляд это однозначное и недвусмысленное указание на то, что использовать её нельзя.
Но, как показано в самом начале, измерение волатильности даже за 5 шагов даёт колоссальную ошибку в 30%! Поэтому, как и при подсчете МОЖ, нам приходится набирать наблюдения в выборку, чтобы повысить точность нашей оценки до каких-то приемлемых значений.
Но вот незадача — предсказательной силой обладает только последняя волатильность, а мы, как по проклятью Гейзенберга, не можем её измерить! Остаётся только идти на компромисс — набирать выборку в не предсказательную глубь, с одной стороны, но преимущественно из последних значений — с другой. ЕМА/АRCH, собственно, эту проблему как-то решают.
На этой балансировке между точностью измерений и точностью прогноза все эти фильтры и держаться. Например фильтр Калмана (он же ЕМА) — вводится для учёта последних изменений, в случае неточности их измерений.
Kot_Begemot, минуточку, коллега. Давайте сначала продемонстрируем, что волатильность имеет АКФ(1)~=1, тогда и будем ломать голову, что с этим делать.
Более того, не вполне очевидно что именно мы должны исследовать: волатильность, или приращения волатильностей? Или, может быть, приращения логарифмов волатильности?
В целом (как бы это не прозвучало парадоксально) меня не очень беспокоит прогноз. А вот вопрос измерения рассматриваю как один из ключевых.
И что такое «измеренная волатильность внутри недельных интервалов»? Как строятся недельные интервалы приращений цен-с пересечением или без?
Очень просто — берём недельный интервал f э (t,t+5) и считаем на нём
std = (f' * f / 5 )^0.5;
Да. Если без пересечений, то точек мало получается. С «обучающей» выборкой не пересекаются.
А что из этого можно вытащить?
А что такое f?
А что такое f?
f — столбец длинной 5 строк логарифмических приращений цен.
Это не означает, что ваш фильтр должен обладать какими-то нестационарными параметрами или работает неправильно, наоборот.
Если говорить о фильтрах, применяемых в технике, то они обычно все частотные ( что не удивительно, так как работают с техническими сигналами), но для фильтрации статистических наблюдений, например контроля положения и скорости объекта в пространстве, используются фильтры с «запаздыванием».
Я же спрашивал о более «слабой» проверке стационарности: проверке стационарности одномерных распределений во временном ряде ошибок.
Среднее разности = 0 или очень близкое к нулю. Но вы спрашиваете о среднем разности во времени.
Это несколько спорное утверждение. Если вы имете модель типа Line Trend, то да — нестационарность ошибки во времени говорит вам о том, что параметры модели должны изменяться во времени вместе с параметрами рынка.
Но для более сложных моделей, например гетероскедастичных (как в случае с волатильностью) ошибка модели уже будет как минимум нестационарна по разбросу (вариации) и это правильно.
Аналогично со смещением ошибки. Если вы рассмотрите связь BR и USD/RUB, например, или любую другую аналогичную связь (Unemployment-Inflation) то из-за особенностей задающего сигнала и, не меньше, из-за частоты измерений вы получите коррелированную ошибку, распределенную во времени нестационарно со смещением.
Вообще говоря, что такое равновесная цена/безработица/ВВП и т.д.? Это цена вокруг которой осуществляется некоторое блуждание, но это блуждание моделируется отнюдь не только белым шумом, но ещё и различными «антиперсистентными» моделями, гасящими ранее накопленное смещение ошибки.
Я так понимаю это t-test ошибок через каждые 10,20,100 отсчётов, так? Нет, такого я не проводил.
Как добить на участки — это вопрос творческий, главное, чтобы были непересекающиеся.
Если Вы считаете, что дисперсия ошибки зависит от значения показателя, значит нужна предварительная нормировка.
Ведь это же просто: если временной ряд ошибок модели неким преобразованием не приводится к стационарному со средним нуль, то предикативная ценность такой модели нулевая.
В том- то и проблема, что стат тесты — дело очень «творческое» и ещё более «творческое» дело их интерпретация.
Если бы это было так, то единственным критерием оптимизации был бы SSE. А в вашем случае, еще и регрессия на SSE, чем я когда-то занимался.
Некоторые модели вообще по определению имеют только положительную или только отрицательную ошибку прогноза, например, если вы предсказываете какое-то событие.
Некоторые модели априорно не могут иметь стационарную ошибку, как, например, прицел на оружии. И т.д.
Простая игра с выигрышами [-1,-1,-1,-1,-1,-1,-1,8] — генеральная совокупность — тоже не будет иметь стационарной ошибки, по крайней мере, вне зависимости от «творческого подхода» в нарезке ряда.
Если вам заранее известно, что ряд стационарен и распределён каким-то симметричным образом, а вы, при этом, предсказываете приращения ряда, то, ваша «простота» в большинстве случаев будет оправдана.
Вот еще цитата: «можно было строить глобальные статистические модели». Но модели чего? Где, в каком месте будет непосредственный выход на портфели/трейдинг?
В данном случае, оговаривается, что модель представляется стационарной и можно пользоваться поправочными методами. Это не означает, что мои решения были получены этим методом — нет, они получены в лоб, решением СЛАУ через обратные матрицы. Но, раз уж мы находим некоторое устойчивое решение, то можно его заменить на Real-Time методы оценки. (Для массивов акций по 3000 эмитентов, то есть для обработки индекса Russel 3000 как раз самое то)
Волатильности. Следующий шаг, частично уже проделанный — ковариации.
Ковариация активов тоже не стационарная величина. Но пока что различными методами прогнозирования — SSA с учётом сезонности, Line Trend и т.п. её спрогнозировать не удаётся. С волатильностью, как оказывается, всё аналогично.
Соответственно, это говорит о некоторой природе ковариации/волатильности и по сути, лучшем методе их оценки. В чём смысл данной работы? Да в том, что ничего лучше уже не придумаешь, чем просто фильтрация входящего сигнала.
Ожидаемые ковариации используются при построении портфелей. Ожидаемые волатильности при прогнозах трендов, если вы считаете, что тренды сопровождаются повышенной волатильностью и при торговле опционами — выходов здесь великое множество.
Eugene Logunov, АКФ модулей returns — это ещё одна отдельная величина. Связана ли она с волатильностью? Безусловно. Но она не является сама по себе волатильностью. А топикстартер (насколько понял) указал мне именно на то обстоятельство, что «АКФ волатильности»достаточно высокое не первом лаге и поэтому усреднение формулой SMA является плохой идеей.
=) Ладно, уже какая-то казуистика пошла. Обменялись мнениями, летим дальше.