SMART-LAB
Новый дизайн
Мы делаем деньги на бирже
Блог им. Kot_Begemot
О применимости АКФ в анализе временных рядов на примере акций ПАО Сбербанк
- 13 июля 2019, 14:22
- |
В свете интереса к моим работам в области оценки рисков нестационарных объектов со стороны опционов и возникшего вопроса о применимости к анализу финансовых временных рядов методов классического статистического анализа проведём маленький численный эксперимент:
- Оценим АКФ акций ПАО Сбербанк за последние 8 лет :
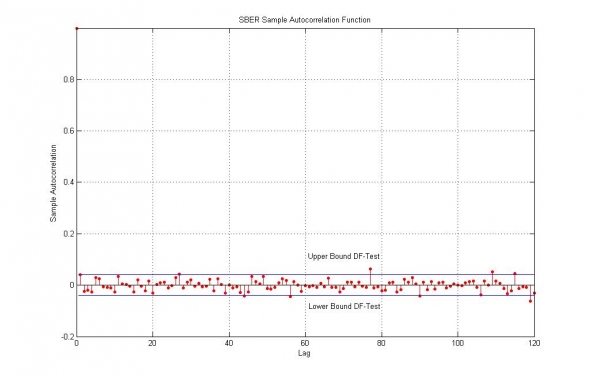
Рис. 1. Тест Дики-Фуллера и автокорреляционная функция логарифмических приращений цен акций ПАО Сбербанк.
Как видно из теста, никаких трендов (англ. тенденций, закономерностей) на акциях Сбербанка классической математической статистикой не обнаружено и все АК коэффициенты лежат в пределе статистической погрешности при измерении нуля.
Однако, тест Дики-Фуллера, с одной стороны, разработан для стационарных, не-локализованных процессов и отражает только отсутствие трендов в среднем по времени, а с другой — проводится совершенно с другими целями выявления детерминированных сезонных и/или растущих тенденций, а не стохастических оценок рисков. В этом смысле мы будем интерпретировать АКФ не по-классически, детерминированно, а как функцию искажения случайности.
Прим. Вышесказанное означает, что любые средства ТА — волновой и свечной анализ, индикаторы и т.д. — будут в лучшем случае проигрывать стратегии «купил и держи» половину доходности (в предположении полу-случайных сделок).
- Построим простейшую нестационарную модель ценообразования:
Пусть S(t) — рыночная цена, являющаяся по отношению к справедливой цене некоторым линейным фильтром и обладающая собственной, дополнительной неустойчивостью — антикоррелированными ошибками определения справедливой экономической цены.
Запишем простейшую AR-1 модель:
dS(t) = acc * dE(t) + (1-acc)*dE(t-1)
где коэффициент асс является корреляционным коэффициентом и отражает конечную точность отражения рыночных равновесных цен через биржевые котировки.
- Оценим глобальную историческую волатильность актива E при помощи кода Матлаб:
% x — исторические данные цен
% L — длина скользящего окна рассмотрения
function s=AdRisk(x,L)
[q]=length(x);
i=L;
while i<q+1
f=x(i-L+1:i);
%% Дисперсии
s(i,1)=std(f); % стандартная оценка
%% Оценка с учётом корреляций
y=f(2:L)-mean(f);
z=f(1:L-1)-mean(f);
c=y'*z/(z'*z);
s(i,2)=std((y-c*z)/(1-c));
end
s(1:L-1,:)=[];
plot(s);
end
- Сравним полученные оценки волатильности (HV) и глобальной волатильности (HV AR adj) актива :

Рис2. Оценки собственной волатильности актива (синяя кривая) и волатильности его справедливых цен (зелёная кривая).
Изображение демонстрирует, что в моменты трендовых движений (выделены вертикальными зонами), когда цены бьют по страйкам, оценка собственной волатильности актива оказывается значительно ниже (на 20-25%) оценки волатильности его справедливых цен.
Историческая волатильность в среднем для акций ПАО Сбербанк занижена на 5% по сравнению с оценкой его глобальной волатильности.
Оценка глобальной волатильности имеет более адаптивную природу и быстрее реагирует на изменяющиеся условия среды.
Это расхождение между волатильностью рыночных и справедливых цен вполне способно объяснить стационарную переоценку опционов, наблюдающуюся на финансовых рынках (превышение IV над HV) :
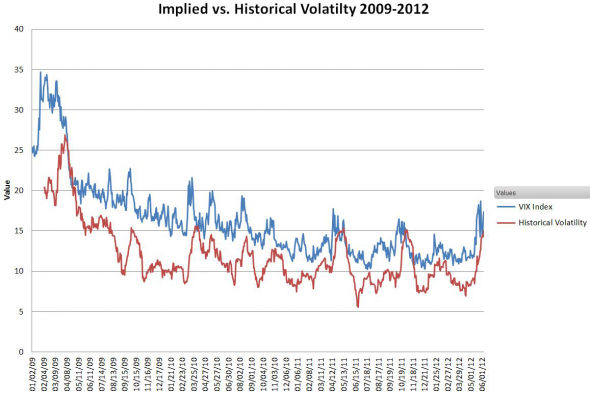
Рис 3. Ожидаемая (VIX) и историческая волатильность опционов на индекс SP500, рассчитанная по 30-дневным опционам биржей CBOE .
3.1К |
Читайте на SMART-LAB:

USD/JPY у 160: рынок проверяет предел прочности иены
Четверг на валютном рынке снова стал днем нефти, в то время как макростатистика отошла на второй план. Рынок активно переоценивает не текущую...
18:36
Пять акций на весну 2026 года
Павел Гаврилов Российский рынок начал 2026 год в плюсе: Индекс МосБиржи прибавил почти 4%. Главные драйверы роста прежние: снижение ставки,...
18:40
теги блога Kot_Begemot
- API
- cpp
- FORTS
- LUA
- Matlab
- NASDAQ
- open source
- Quik Lua
- S&P
- S&P500
- S&P500 фьючерс
- Vanguard Group
- VIX
- акции
- акции США
- алгоритмы
- алготрейдинг
- анализ временных рядов
- баффет
- волатильность
- Гордон
- доверительное управление
- долги
- игры
- инвестиции
- индекc
- интеграция
- искусственный интеллект
- Келли
- Книги
- книги о трейдинге
- корреляция
- кризис
- криптовалюта
- лудомания
- Марковиц
- матлаб
- машинное обучение
- ММВБ Акции
- наука
- нейронные сети
- облигации
- одураченные случайностью
- оптимизация
- оптимизация торговых систем
- опционы
- оффтоп
- оционы
- памм счета инвестиции
- паника
- пирамида
- ПИФы
- портфели
- Портфель
- портфельное инвестирование
- пузыри
- раздача
- рецензия
- Риски
- рэнкинг мосбиржи
- Сбербанк
- спекуляции
- статистика
- стоимостное инвестирование
- талеб
- теги не нужны
- теория игр
- торговая система
- торговые роботы
- трейдинг
- улыбка волатильности
- управляющая компания
- финанализ
- фундаментальный анализ
- фьючерс ртс
- Шарп
- шутка
- Экономика





















Но если говорить о VIX и явной трендовости SPX 09-11, то можно и так интерпретировать, что опционы торгуются вполне по справедливой цене.
А так, чтобы можно было купить c 5 плечом и забыть или поиграть на откатах — нет, такого в Сбербанке не было. (как считает математика)
Там есть другая штука про тренды… позволяющая им появляться безо всякой АКФ (стохастический тренд) о чём в основном тексте специально сделана оговорка. Что, собственно, нам и нужно — какой смысл анализировать риски детерминированных трендов (даже если цена стоит на одном месте), если их, рисков, попросту нет?
Не обязательно. Могут быть какие-то сезонные колебания ещё или даже параболы — всё что можно квалифицировать отдельно от шума и есть тренд. В данном случае АКФ говорит что в каждый из 8 годов вероятность роста одинакова и составляет около 10% годовых — грубо говоря так. Покупайте в любое время — всё будет одинаково. Принцип купить на падении или купить на росте — не работает.
Я несколько поменял вводную, чтобы было понятнее.
Но в качестве дополнения АКФ/ SSA / Фурье использовать можно. Как основу системы — нет.
Коррекция -это фсегда (!!) четное количество новых перемен 2-4-8.Просто надо учиться у японцев читать график. Я называю это- танец цены 3-2 те 3 шага вперед и 2 назад.
Безо всякой математики в любом графике котировок можно увидеть сколько угодно «трендов» различной, заранее заданной «силы». Индикатор «Зигзаг» отлично эти «тренды» показывает.
А под «силой тренда» можно понимать ту процентную величину, которую «Зигзаг» учитывает для отрисовки очередного экстремума, после того как котировки уйдут против этого экстремума на этот процент. Если повезёт, котировки могут уйти по новому тренду после точки поворота очень далеко — на радость игроку, поймавшему этот новый тренд.
Реальны только прошедшие тренды. Тренды в будущее — только в воображении.
Мой индикатор Зигзаг (PeakAnTrough) для Quik'а, показывающий всевозможные тренды на любой истории котировок, можно скачать с
forum.quik.ru/forum17/topic3433/