Сложности больших тайм-фреймов (дни, недели)

Положительные моменты стратегий на больших тайм-фреймах: большая, по сравнению с малыми тайм-фреймами,  вероятность выигрыша (от60% и выше); возможность работать не спеша, осмысливая все риски и сложности.

Отрицательный момент – малое количество сделок: На нашем рынке получается (во всяком случае у меня) обычно около 10. Практически все инструменты пляшут под одну дуду и идут в одну ногу: нет возможности игры на разных инструментах, — все растут и падают практически одновременно. На международных рынках, наверное, можно периодически равномерно в течение года отыскивать благоприятные возможности и, таким образом, повышать число заходов.

Итак, пусть вероятность выигрыша р=60%, величина выигрыша и проигрыша одинакова k=1:1, в год 10 заходов, играем три года. Какова вероятность не получить за три года никакого выигрыша (т.е. выигрыш «0» и меньше)? Можно точно посчитать по ф.Бернулли: 17.5%. На рис.1 показаны вероятности выигрыша «n» раз за 30 входов в рынок (наиболее вероятно выиграть 18 раз).

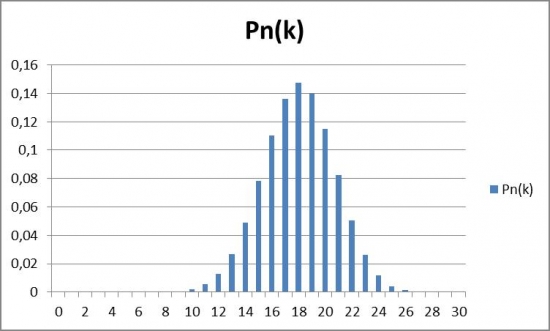
Рис.1. Вероятности выигрыша «n» раз за 30 входов в рынок

Можно понять чувства трейдера, тщательно игравшего выигрышную стратегию три года и не получившего прибыль.

На рис.2 показана одна случайная симуляция процесса игры по этой стратегии. То, что просадка по одной из реализаций составила 10 пунктов – это ерунда, по сравнению с флэтом, который длился для двух случаев почти 100 заходов.

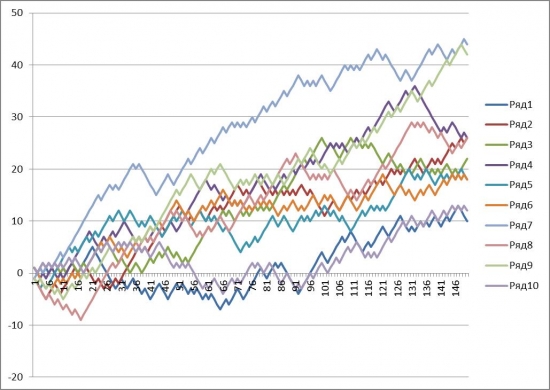
Рис.2. Случайная симуляция игры с параметрами р=60%, k=1:1.

Не зная этих неприятных нюансов, очень многие трейдеры не выдерживают и сходят, а в принципе стратегия, то выигрышная.

Вывод: или повышайте вероятность выигрыша или увеличивайте число заходов, или терпите (или бежите прочь!).