SMART-LAB
Новый дизайн
Мы делаем деньги на бирже
Блог им. olegal20111
Улыбка волотильности
- 27 февраля 2018, 20:04
- |
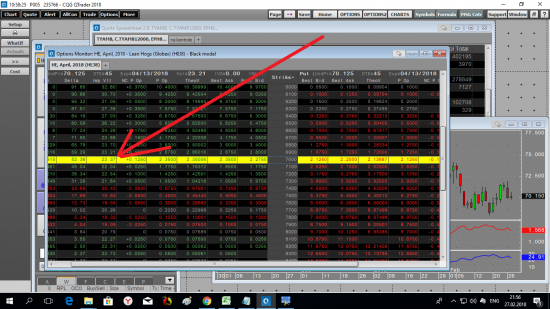
Подскажите: почему волатильность распределяется не равномерно, то есть равномерно/одинакова не увеличивается в обе стороны одинаково?
40 |
Читайте на SMART-LAB:

Софтлайн полностью погасил пятый выпуск облигаций
Друзья, рады сообщить, что сегодня мы полностью погасили выпуск облигаций серии 002Р-01 на сумму 6 млрд рублей. Все обязательства перед...
13:44

Вышел эфир RENI для Bazar
Благодарим платформу Bazar за приглашение на разговор! Хотя, видео вышло с заголовком «Шокирующая правда о рынке страхования в 2026 году |...
11:59




















Рассмотрим логнормальное случайное блуждание:
где dX — Винеровский процесс.
Определим вероятность того, что цена из начальной точки S во время t окажется в диапазоне от a до b во время t':
( Читать дальше )
- комментировать
- Просмотры 2 за час / 94 за сутки / 3988 за неделю | ★14
- Комментарии(110)
Функция нормального распределения в формулах стоимости опционов- 25 февраля 2018, 15:21
- |
- bstone
- Сохр
- |
- Ж
- |
- Печать
Попробую доступно показать, откуда берется в формулах стоимости опционов функция распределения Гаусса.Итак исходное уравнение Блэка-Шоулза:
где V — цена опциона, S — цена спота, r — ставка, ну и сигма в представлении не нуждается.
Это параболическое дифференциальное уравнение в частных производных. Решать можно несколькими способами, но я не буду этого делать, а сразу запишу решение, т.к. его вывод не имеет значения для цели этого топика.
Чтобы слегка упростить запись, введу переменную времени, оставшегося до экспирации:
Решение уравнения БШ тогда можно записать в следующем виде:
где Payoff(S) — это функция выплат опциона. Для опциона кол:
Соответственно цена кола:
поменяем переменную интегрирования на
тогда
Считать стоимость опциона по этой формуле не очень просто, но рассмотрим сначала второе слагаемое:
Сложно не заметить сходство с функцией нормального распределения:
В силу популярности нормального распределения для этой функции существует немало аппроксимаций и способов вычислить ее численно. Та или иная реализация имеется, без преувеличения, в любом статистическом пакете.
Если нам удастся выразить второе слагаемое через эту функцию, то считать стоимость опционов будет намного легче. Так что овчинка стоит выделки!
Заменим переменную интегрирования во втором слагаемом выше на
и получим
где
С первым слагаемым не так очевидно, но все же не очень сложно. Сначала надо подвести дополнительное слагаемое в экспоненте под квадрат, а далее действуем аналогично второму слагаемому. Поэтому здесь я сразу запишу результат:
где
В итоге получаем, что хотели:
Но так как распределение БА не нормальное, то его надо скорректировать улыбкой. А она на дельту влияет. Поэтому так и получается.
И почему с 7400 по 7900 идет какой то перепад волотильности?
Прошу подсказать если кто то знает
Ты почитай где нибудь про распределения, случайности, вообще про опционы и вопросы снимутся. А сей час продай дорогие путы и купи дешевые колы и профит обеспечен.