Блог им. kulakov74
Доходность к погашению (Yield to maturity, YTM)
- 12 января 2018, 00:19
- |
Давно хотел понять, что такое доходность к погашению, но всё никак руки не доходили. Одно дело, когда тебе квик/сайт ММВБ показывает какое-то число, типа 5.25%, и вроде оно и должно быть правильным, но что за этим стоит? И что это означает на практике? В инете есть сложные формулы доходности, и (если сможешь разобраться) они вроде считают приблизительно то же самое, но, опять же, почему они именно такие, как они получены? Хочется, чтобы этот процент, какой бы он ни был, можно было напрямую сравнивать со ставками банковских вкладов, потому что это просто и понятно.
Зачем нужно уметь считать доходность самому?
- Чтобы проверить, что она на самом деле такая.
- Чтобы учесть налог на купон для корпоративных бумаг, т.к. в квике он не учитывается.
- Чтобы учесть комиссию.
- Чтобы посчитать доходность для бумаг, по к-м нет торгов на бирже (есть на внебирже) и поэтому в квике показывается 0.
- Можно посчитать для любой цены или даты.
Сразу скажу, что самый простой способ посчитать доходность – это использовать функцию ДОХОД в Excel. Для примера я буду использовать еврооблигацию GAZPR-34 на 10.01.18 с ценой 137.5 и НКД 17,7292. В данном случае ф-я ДОХОД получает 4,284% (тут учитывается налог), но при этом она требует очень мало параметров:
ДОХОД(дата покупки; дата погашения; ставка купона; цена;100; 2; 0)*100.
НКД она считает сама. Есть и отдельная функция для подсчета НКД — НАКОПДОХОД(). Кроме того, в Excel есть и другие функции, к-е могут оказаться полезными:
ДАТАКУПОНДО/ДАТАКУПОНПОСЛЕ – определяют дату предыдущего/следующего купона
ЧИСЛКУПОН — число оставшихся купонов.
Сначала я (наверное, как и многие) предполагал, что тут весь фокус в капитализации и реинвестировании купонов, и даже стал считать таким образом доходность в Excel. Цифры получались близкие к тем, что показывал квик, но всё же не те, тем более, что по некоторым бумагам они отличались значительно.
Затем я придумал интервальный способ подсчета, в котором весь период времени до погашения разбивается на интервалы длиной полгода (между купонами), и доходность считается для каждого из них, а затем получается средневзвешенная дох-ть для всего периода. Здесь делается предположение, что цена с момента покупки до погашения равномерно снижается (или увеличивается) до номинала. Зная количество дней до погашения и текущую цену, можно получить предполагаемое изменение цены за 1 день, и за любое число дней, а значит – и в день выплаты каждого купона. А зная последние, можно для каждого интервала получить:
- Сумма вначале (цена)
- Сумма в конце (цена в конце + купон)
- Разница, процент и годовой процент
Для самого 1-го периода ситуация несколько усложняется НКД, но это не принципиально. Далее, получив для каждого интервала годовой процент и зная цену в его начале, можно получить средневзвешенный годовой процент за всё время (используя цену как вес т.к. она всё время меняется). Полученное значение уже больше похоже на то что показывает квик, но и оно немного отличается. Проблема в том, что оно начинает заметно меняться, когда от даты покупки до первого купона остается мало времени, особенно, если учесть комиссию. Причина оказывается в том, что т.к. длина интервала в днях тоже разная её тоже надо учитывать как вес. При добавлении её в расчеты результат перестает зависеть от длины первого интервала. В Excel всё это выглядит примерно так (здесь не учитывается НДФЛ):
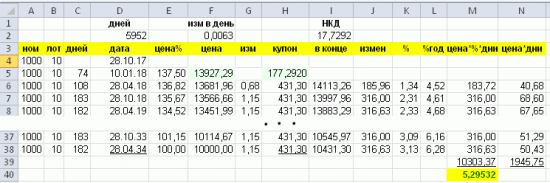
Проблема с этим способом состоит в том, что он основан на предположении, что цена идет к номиналу равномерно, а в реальности это не так, и в идеале определение доходности от цены зависеть не должно.
В какой-то момент попался пост на эту тему anatolyutkin «Еврооблигации и депозиты», к-й дал подсказку. На самом деле там всё написано, но т.к. у меня в финансовой области образования нет, то я его сразу осилить не смог, тем более что там в расчётах используется Бином Ньютона и т.п., но всё же я понял основную идею – текущая стоимость. Оказывается, это такой финансовый термин, к-й означает сколько нужно вложить сегодня, чтобы через какое-то время получить заданную сумму. Фокус в том, что обычно расчет производится наоборот – имеем сумму, например 1000р, процент (8%), и через год получаем 1080р. А здесь известно, сколько будет в конце и процент, а найти надо, сколько было вначале.
Ну а дальше основной финт мозгами состоит в том, чтобы понять, что когда вы покупаете облигацию (затраты = текущая цена + НКД), вы как бы открываете много маленьких вкладов на разные сроки. Вкладов столько, сколько вы получите купонов + еще 1 для номинала. Каждый вклад закрывается, когда вы получаете по нему купон, и все вклады имеют одинаковый процент.
Но здесь есть 1 нюанс – считать нужно так, как будто эти вклады имеют капитализацию. Её на самом деле конечно нет, но это нужно делать для того, чтобы полученный процент соответствовал каким-то общепринятым ориентирам. Если нам нужно сравнить доходность с обычными вкладами, то можно использовать годовую капитализацию. С другой стороны,
In a number of major markets (such as gilts) the convention is to quote annualised yields with semi-annual compounding
Что означает, что существует соглашение указывать доходность с полугодичной капитализацией, так что можно посчитать и так. Понятно, что из-за более частой капитализации процент доходности будет немного ниже. В квике, на сайте ММВБ и в функции ДОХОД доходность вычисляется именно так. Формула для расчета начальной суммы отдельного вклада для годовой капитализации выглядит так:
Sum=EndSum / ((1+Rate/100)^Years) / (1+Rate/100*YearPart)
Здесь EndSum – купон или номинал, Rate – искомый процент, Years — число полных лет вклада, YearPart – дробная часть лет. Для полугодичного варианта:
Sum=EndSum / ((1+Rate/200)^YearHalves) / (1+Rate/100* YearHalfPart)
Здесь YearHalves – число полных полугодий, YearHalfPart — дробная часть полугодий. Далее, если просуммировать все начальные суммы этих вкладов, то должно получиться число, равное первоначальным затратам, т.е. текущая цена + НКД. Другими словами, тут нельзя получить формулу типа Rate=… где доходность вычисляется одним выражением – нужно подбирать разные значения до тех пор, пока результат не будет отличаться от требуемого на величину типа 0.00001. В Excel это выглядит так (здесь НДФЛ уже учтен, при этом для простоты в НКД он тоже учтён):
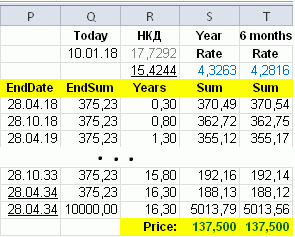
Конечно, так рассчитывать доходность не нужно, это просто для понимания. В интернете также можно найти более простые формулы для расчета доходности без суммирования, в к-х присутствует параметр «общее количество купонных платежей», но при этом не учитывается НКД. Кроме того, на сайте ММВБ есть документ «Методика расчета НКД и доходности», содержащий формулу доходности с параметром «число дней». Этот параметр делится на число дней в году, т.е. получается число лет, т.о., данная формула получает доходность с годовой капитализацией, и это не та величина, к-я показывается на этом же сайте для конкретных бумаг.
Еще раз скажу про заблуждение насчет реинвестирования – оно в расчете ДП не учитывается:
A common misconception is that the coupons must be reinvested at the yield to maturity… making this assumption is a common mistake in financial literature and coupon reinvestment is not required for YTM formula to hold.
(Вики)It is a chronic error in that it persists in spite of continued attempts to correct it. For example, Renshaw addressed this error fifty years ago … but the reinvestment assumption continues to be replicated. … successive generations of financial professionals educated with the erroneous text have restated the claim in materials intended to educate investors….
Among the sites containing this claim are Bloomberg.com,… Investopedia.com, Morningstar.com, and even the popularly edited Wikipedia.org…
(«Yield-to-Maturity and the Reinvestment of Coupon Payments»)
Получаемая величина ДП, например 4.3%, означает только процент, к-й начисляется на вложенные средства только пока вы владеете данной ЦБ. Как только вы получили деньги (купон) назад, этот процент начисляться перестает а его новые инвестиции к нему никакого отношения не имеют. Разница только в том, что в случае обычного вклада вы получаете сразу всю сумму назад с процентами, а здесь как бы есть много маленьких вкладов под одинаковый процент и вы получаете их по одному постепенно.
Т.к. нам более привычна ситуация когда вся сумма возвращается сразу, можно попытаться посчитать и т.н. реальную доходность с учетом последующего (ре)инвестирования купонов (необязательно в ту же ЦБ) до погашения. Для каждого купона срок его реинвестирования равен
ReinvDays=EndDate-CouponDate
где EndDate – дата погашения и CouponDate – дата выплаты купона. Сумма, к-я получается в результате реинвестирования купона рассчитывается по формуле:
ReinvSum = Coupon * ((1+ReinvRate/100)^ReinvYears) * (1+ReinvRate/100*ReinvYearPart)
(здесь подразумевается ежегодная капитализация). Если просуммировать все такие суммы, а также последний купон и номинал, то получится итоговая сумма за весь срок до погашения. Зная начальную (Sum1=цена + НКД) и конечную сумму EndSum, а также срок, можно подобрать ставку, к-я даст такой результат, используя ту же формулу:
EndSum = Sum1 * ((1+RealRate/100)^TotalYears) * (1+RealRate/100*TotalYearPart)
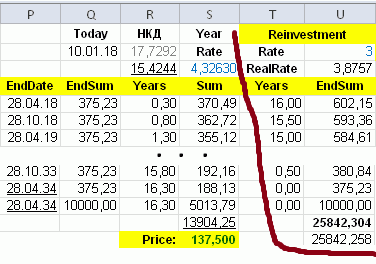
Очевидно, что на практике реинвестировать под ту же ставку не получится, поэтому можно просто рассмотреть разные варианты для оценки. Для того же примера с ДП = 4,3263%:
- Если ReinvRate=0 (купоны вообще не инвестируются), то RealRate=2,96%
- Если ReinvRate=3%, то RealRate=3,876%
- Если ReinvRate=Rate=4,3263%, то реальная дох-ть будет такой же
- Если ReinvRate=5%, то RealRate=4,567%
Как видим, ставка реинвестирования влияет на итоговую реальную доходность.


теги блога СергейК
- chrome
- Javascript
- QUIK
- rus еврооблигации рф
- RUS-28
- YTM
- автологин
- биржа
- бонусы
- браузер
- брокер Открытие
- брокеры
- валютная переоценка
- война
- выплата купона
- дефолт облигаций
- доходность к погашению
- еврооблигации
- золото
- Инвестиционная палата
- Интерфакс
- история
- квалифицированный инвестор
- квик
- колл-опционы
- комиссия
- кредитное плечо
- купон
- ЛДВ
- Минфин
- налог
- налогообложение на рынке ценных бумаг
- О'КЕЙ
- Облигации
- открытие брокер
- оферта
- оффтоп
- Парсер
- плечо
- программа лояльности
- расширение
- сайт
- санкции
- смартлаб конкурс
- ссылки
- Сэтл-Групп
- трейдинг
- эбис
- экономика России
- эмитенты
- япония





















Налог = (цена в рублях при продаже (T+2, без НКД) минус то же самое при покупке минус все комиссии)*0.13. Не забывайте про правило FIFO (ЦБ продаются в порядке приобретения). Если продажа через 3 года и более — налог 0.
спасибо заранее. infant05@mail.ru
Дюрация — это средний объем общих платежей по долговой бумаге, начиная от сегодняшнего дня до момента ее погашения. С ростом количества потенциальных выплат возрастает и коэффициент дюрации. Чем больше коэффициент дюрации, тем выше процентный риск облигации и наоборот.
Процентный риск – это зависимость от процентной ставки. Цена облигации с более длительным сроком до погашения будет иметь более сильную зависимость от процентной ставки, чем цена облигации, выплаты по которой произойдут в ближайшем будущем. Это связано с тем, что при расчете дюрации платежи по облигации оцениваются с учетом удешевления денег со временем.
В условиях ожидаемого повышения процентных ставок, оптимальными для инвестиций являются облигации с меньшей дюрацией. Они упадут меньше в цене, чем облигации с большим значением дюрации.
Если ожидается, что процентные ставки будут снижаться, то следует выбирать облигации с большей дюрацией. Когда доходность облигаций снижается, а цены растут, такие бумаги чувствуют себя стабильнее и падают меньше в цене.
Ну и зачем выходить, если вы купили при дохе в 4%
Что касается интервального метода определения ДП, то его не сложно модифицировать так, что он будет давать более точный результат. Как видно из картинки выше, в оригинальном варианте годовой процент все время увеличивается. Можно применить тот же подход, что и в основном варианте: вместо вычисления дох-ти данного интервала, предполагаем, что она у всех интервалов одинаковая, и подбираем её. Для каждого интервала известна начальная цена, доходность и купон. Конечная цена вычисляется по формуле:
EndPrice=Price*(1+YTM/100/365.25*Days)-Coupon;
Т.о., каждый интервал за счет доходности уменьшает цену. В конце концов она должна быть равной номиналу. Если это не так, то пробуем другое значение, и т.д. В результате, т.к. у всех интервалов одинаковая дох-ть, никакие веса учитывать не нужно. А получаемое значение почти такое же, как в основном варианте с полугодовой капитализацией.