Эмпирические методы управления капиталом: разбор книги Ральфа Винса “Математика управления капиталом”

Команда DTI подготовила краткое изложение книги Ральфа Винса “Математика управления капиталом” с нашими комментариями. Раз в неделю будем публиковать отдельные обзоры каждой главы.

Сегодня разбираем первую главу “Эмпирические методы”. В ней даются базовые понятия, такие как HPR, TWR, оптимальная доля портфеля, процесс независимых/зависимых испытаний, серийные тесты, доверительная граница/интервал. Подчеркивается важность оптимальной доли счета для торговли = оптимальное “f”. Сделан акцент на соотношении риска и задействованного в торговле объема капитала.

Определения

HPR (holding period returns) — доход за период удержания позиции. Например HPR = 1,10 означает, что сделка за данный период принесла прибыль в 10%.

AHPR — средняя арифметическая прибыль без реинвестирования.

GHPR — средняя геометрическая прибыль с учетом реинвестирования.

TWR (technical wealth relative) — относительный конечный капитал. Значение этого показателя отражает во сколько раз был увеличен первоначальный капитал. TWR за ряд периодов или сделок равняется перемножению всех входящих в него HPR.

Эконометрические показатели

Отдельно рассматривается понятие корреляций. На протяжении всей книги активно используется коэффициент корреляции Пирсона. Значение коэффициента корреляции колеблется в пределах от -1 до +1. Чем ближе коэффициент корреляции к ± 1, тем сильнее зависимость. Положительная корреляция — движение в одну из сторон по одному активу сопутствует движению в ту же сторону по второму. То есть, большие выигрыши редко сменяются большими проигрышами. Отрицательная корреляция — движения противоположны. То есть, большие проигрыши часто сменяются большими выигрышами и наоборот.

Пример положительной и отрицательной корреляции цен двух активов:

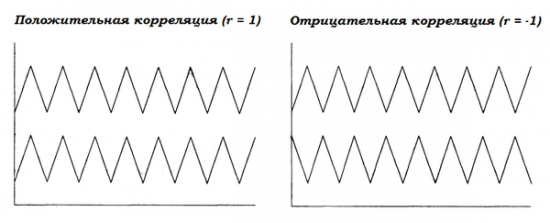
Говоря о зависимостях внутри одной торговой системы, Винс делает акцент на том, что необходимо избавляться от любых зависимостейторговых прибылей и убытков друг от друга. Если такие зависимости существуют, значит, торговая система не до конца оптимизирована и требует доработки.

Вместе с корреляциями рассматривается математическое ожидание(МО). Подчеркивается важность и необходимость выборки систем с максимально положительным МО, так как системы с отрицательным МО заранее проигрышны. При этом приводится интересный факт, что при наличии 2 систем одна из которых имеет положительное МО, а другая отрицательное, их возможно использовать в паре и сделать из них единую прибыльную систему с положительным МО, при условии, что у данных систем будет отрицательная корреляция (чем более отрицательная, тем лучше).

Перспективы реинвестирования

Затрагивается вопрос о целесообразности реинвестирования. Особенность реинвестирования заключаются в том, что реинвестирование улучшает не каждую торговую систему и необходимо проводить дополнительные тесты. Хорошим показателем пригодности торговой системы для реинвестирования является высокий показатель среднего геометрического. Среднее геометрическое (СГО) — это корень N степени (N — количество периодов/сделок) из относительного конечного капитала (TWR), то есть, по сути, фактор роста счета. СГО > 1 говорит о пригодности системы для реинвестирования, СГО < 1 означает, что система непригодна для реинвестирования и, более того, может из прибыльной системы сделать убыточную.

Оптимальная доля для торговли

При торговле необходимо выбрать количество контрактов для покупки. Это зависит в том числе от общего количества вкладываемых денег и от возможных потерь. Для определения количества контрактов используется делитель максимально возможных потерь — f. Он может принимать значения от 0 до 1.

Пример определения количества контрактов:

Далее обсуждается тема торговли оптимальной долей портфеля — оптимальное f. Сначала рассматривается система торговли фиксированной долей портфеля. Первый вариант расчета оптимального f — формулы Келли. Однако они дают достоверные результаты только в случае, когда результаты имеют распределение Бернулли (бинарное распределение), что несвойственно для торгового процесса, и, следовательно, не может использоваться в торговле. Второй вариант поиска — перебор значений f от 0,01 до 1 и выявление наибольшего TWR или СГО (не имеет значения, так как пики будут совпадать).

Пример зависимости TWR от f для 20 игр, в которых можно выиграть $2 или проиграть $1:

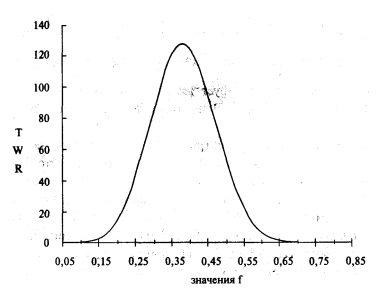
Получив значение оптимального f, необходимо разделить максимальный проигрыш на отрицательное значение оптимального f. Полученное значение будет показывать, какой капитал стоит задействовать на один контракт. Соответственно, чтобы получить оптимальное количество контрактов для торговли по счету, необходимо размер счета разделить на полученное значение капитала на один контракт. Важно, что разница в торговле с использованием оптимального f и без него заметна только на дистанции (чем больше количество сделок, тем сильнее эффект оптимального f).

Значимым показателем прибыльности торговой системы также является средняя геометрическая сделка (то есть средняя прибыль на сделку). При условии, что торговля ведется фиксированной долей счета, этот показатель становится равен МО на сделку. МО = СГО — 1.

Особенностью оптимального f, является то, что чем больше значение оптимального f, тем больше потенциальный максимальный проигрыш торговой системы (в % от счета). Более того, максимальный проигрыш не может быть меньше оптимального f (в % от счета).

Модель Марковица

Для того, чтобы минимизировать возможные проигрыши, необходимо диверсифицировать портфель с учетом корреляций между активами/стратегиями, а также оптимального f. При этом, для создания максимально эффективного портфеля, в него необходимо включать стратегии/активы с максимально отрицательной корреляцией. Также важно отметить, что чем выше корреляция, тем меньше дисперсия результатов, а, следовательно, и потенциальный риск.

За основную концепцию формирования портфеля принимается модель Гарри Марковица. Марковиц предположил, что инвесторы действуют рационально и при наличии выбора предпочитают портфель с меньшим риском при равном уровне прибыльности или выбирают портфель с большей прибылью, при одинаковом риске. Марковиц утверждает, что для данного уровня риска есть оптимальный портфель с наивысшей доходностью, и таким же образом для данного уровня доходности есть оптимальный портфель с наименьшим риском.

Портфель, доходность которого может быть увеличена без сопутствующего увеличения риска или портфель, риск которого можно уменьшить без сопутствующего уменьшения доходности, согласно Марковицу, неэффективны.

Эффективные (например, A и B) и неэффективные (например, C) портфели:

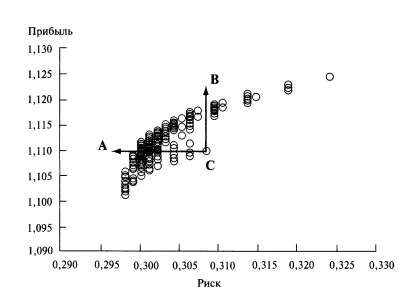
Марковиц ввел понятие “эффективная граница”. Это набор портфелей, которые находятся в верхней левой части графика, то есть портфели, прибыль которых больше не может быть увеличена без увеличения риска, и риск которых не может быть уменьшен без уменьшения прибыли. Портфели, находящиеся на эффективной границе, называются эффективными портфелями.

Граница эффективных портфелей:

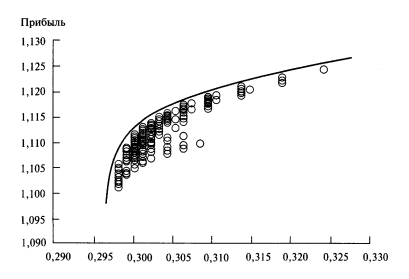
Портфели, которые находятся вверху справа и внизу слева, в целом недостаточно диверсифицированы по сравнению с другими портфелями. Те же портфели, которые находятся в середине эффективной границы, обычно очень хорошо диверсифицированы. Выбор портфеля инвестором зависит от степени неприятия риска инвестором — иначе говоря, от желания взять на себя риск. В модели Марковица любой портфель, который находится на эффективной границе, является хорошим выбором.

Продолжение статьи читайте в Блоге DTI